В данной теме ознакомимся с приемами формализации сложных высказываний, интерпретацией формул логики высказываний и построением истинностных таблиц.
Математическая логика рассматривает языки, основная цель которых-обеспечить символизм (систему формальных обозначений) для рассуждений, встречающихся не только в математике, но и в повседневной жизни. Простейшей математической логикой является логика высказываний (ЛВ), более общей системой - логика предикатов (ЛП) или логика первого порядка. Высказывание - это повествовательное предложение, которое может быть либо истинным, либо ложным, но не тем и другим одновременно. Примеры высказываний: ”Снег белый”, ”Сахар ¾ углеводород”. ”Истина” или ”Ложь”, приписанная некоторому высказыванию, называется истинностным значением этого высказывания. Обычно обозначают “истину” через 1, ”ложь” - через 0. Высказывания могут обозначаться таким образом: P 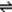 Снег белый; Q
Снег белый; Q 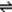 Сахар ¾ углеводород.
Сахар ¾ углеводород.
Символы P и Q и т. д., которые используются для обозначения высказываний, называются атомарными формулами или атомами. Из атомарных высказываний строят составные (сложные) высказывания, используя пять логических связок: 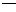 (не), отрицание;
(не), отрицание; 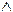 (и), конъюнкция (а, но, а также);
(и), конъюнкция (а, но, а также); 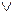 (или), дизъюнкция;
(или), дизъюнкция; 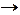 (если,..., то), импликация;
(если,..., то), импликация; 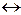 (тогда и только тогда, когда), эквиваленция. Иногда может употребляться связка
(тогда и только тогда, когда), эквиваленция. Иногда может употребляться связка 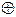 (или... или), строгая дизъюнкция или сложение по модулю 2 (mod2). Эти связки можно использовать для построения все более сложных составных высказываний путем повторного применения связок к уже имеющимся высказываниям.
(или... или), строгая дизъюнкция или сложение по модулю 2 (mod2). Эти связки можно использовать для построения все более сложных составных высказываний путем повторного применения связок к уже имеющимся высказываниям.
В ЛВ правильно построенные формулы (ППФ) определяются рекурсивно следующим образом:
1) атом есть формула (P,Q,....);
2) если P-формула, то (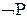 ) -также формула;
) -также формула;
3) если P и Q -формулы, то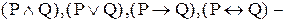 также
также
формулы;
4) никаких формул, кроме порожденных применением указанных выше правил, нет.
Например,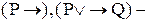 это не формулы. Можно обходиться без некоторых скобок в формулах, приписывая убывающий ранг пропозициональным (логическим) связкам в следующем порядке:
это не формулы. Можно обходиться без некоторых скобок в формулах, приписывая убывающий ранг пропозициональным (логическим) связкам в следующем порядке:
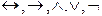
и требуя, чтобы связка с большим рангом всегда имела большую область действия.. Таким образом,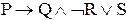 означает
означает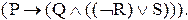
Пусть G и H - две атомарные формулы. Тогда истинностные значения формул 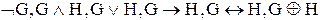 связаны с истинностными значениями формул G и H так, как это показано в табл. 9.1:
связаны с истинностными значениями формул G и H так, как это показано в табл. 9.1:
Таблица 9.1 - Истинностные значения для 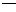 ,
, 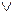 ,
, 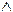 ,
, 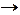 ,
, 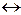 ,
, 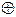
| G H | 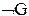 | 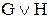 | 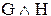 | 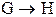 | 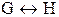 | 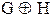 |
| 0 0 | ||||||
| 0 1 | ||||||
| 1 0 | ||||||
| 1 1 |
Основываясь на этой таблице, удобно описывать способы вычисления истинностных значений формулы по истинностным значениям атомов, входящих в эту формулу.
Например, для формулы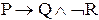 имеем: пусть Р=1,Q=0,R=0, тогда
имеем: пусть Р=1,Q=0,R=0, тогда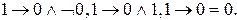
Приписывание истинностных значений атомам, входящим в формулу, называется интерпретацией формулы. Каждому из атомов можно приписать 0 или 1. Тогда, если в формуле имеется n атомов, то она имеет 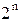 интерпретаций. Таблицу 9.1, в которой указаны истинностные значения формулы Р при всевозможных истинностных значениях атомов, встречающихся в Р, называют истинностной таблицей формулы Р.
интерпретаций. Таблицу 9.1, в которой указаны истинностные значения формулы Р при всевозможных истинностных значениях атомов, встречающихся в Р, называют истинностной таблицей формулы Р.
Говорят, что формула Р истинна при некоторой интерпретации, тогда и только тогда, когда Р получает значение 1 в этой интерпретации, в противном случае говорят, что Р ложна при этой интерпретации. Формула ЛВ общезначима тогда и только тогда, когда она истинна при всех возможных интерпретациях. Формула ЛВ противоречива (или невыполнима) тогда и только тогда, когда она ложна при всех своих интерпретациях. Формула непротиворечива (или выполнима) тогда и только тогда, когда она не является противоречивой.
Если формула F истинна при интерпретации I, то говорят, что I удовлетворяет F, или F выполнена в интерпретации I. С другой стороны, если формула F ложна при интерпретации I, то говорят, что I опровергает
F, или F опровергается в I. Например, формула 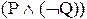 выполнена в
выполнена в
интерпретации 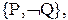 но опровергается в интерпретации
но опровергается в интерпретации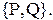 Когда
Когда
интерпретация I удовлетворяет формуле F, I называется также моделью F.
Доказательство общезначимости или противоречивости формул ¾ очень важная задача. В ЛВ ввиду конечности числа интерпретаций путем полного перебора всех возможных интерпретаций всегда можно решить, общезначима (противоречива) ли формула.
Рассмотрим примеры решения типичных задач и упражнений:
1. Формализовать средствами ЛВ предложение: ”Если влажность большая и температура высокая, то мы не чувствуем себя хорошо”.
Решение. Выделим в данном предложении атомарные высказывания:
Р 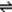 Влажность большая;
Влажность большая;
Q 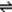 Температура высокая;
Температура высокая;
C 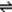 Мы чувствуем себя хорошо.
Мы чувствуем себя хорошо.
Тогда исходное предложение можно записать в виде составного высказывания: 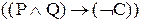 или
или 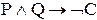 .
.
2. Записать в виде формулы ЛВ следующую теорему: ”Если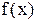 непрерывна на интервале I, и если
непрерывна на интервале I, и если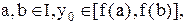 то тогда на
то тогда на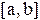 существует хотя бы одна точка
существует хотя бы одна точка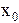 такая,что
такая,что 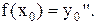
Решение. Выделяем атомарные высказывания:
X 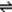
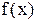 непрерывна на интервале I;
непрерывна на интервале I;
Y 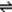
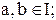
Z 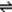
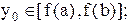
T 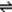 на
на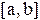 существует хотя бы одна точка
существует хотя бы одна точка 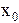 ;
;
K 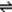
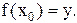
Формула данного сложного высказывания запишется:
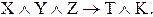
3. Заполните истинностную таблицу для формулы ЛВ:
G 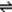
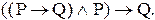
Решение. Атомы этой формулы ¾ Р и Q. Следовательно, формула имеет 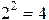 интерпретации. Истинностные значения G при всех ее интерпретациях приведены в табл.9.2.:
интерпретации. Истинностные значения G при всех ее интерпретациях приведены в табл.9.2.:
Таблица 9.2 - Истинностная таблица для 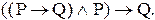
| P Q | 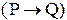 | 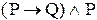 | 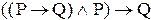 |
| 0 0 | |||
| 0 1 | |||
| 1 0 | |||
| 1 1 |
Как видим, формула G истинна при всех интерпретациях, т.е. общезначима. Такую формулу еще называют тавтологией.
4. Построить истинностную таблицу для формулы
G 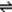
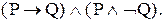
Решение. Истинностная таблица для G дана в табл.9.3. Как видим, эта формула ложна при всех интерпретациях, т. е. противоречива.
Таблица 9.3 - Истинностная таблица для 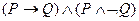
| P Q | 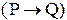 | 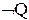 | 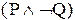 | 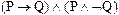 |
| 0 0 | ||||
| 0 1 | ||||
| 1 0 | ||||
| 1 1 |
Контрольные вопросы и задания по теме:
1. Логика высказываний.
2. Высказывания, логические связки, логические парадоксы.
3. Составные высказывания.
4. Истинностные значения и функции.
5. Формулы ЛВ. Интерпретации формул ЛВ. Таблицы истинности формул ЛВ.
6. Общезначимые, противоречивые и выполнимые формулы ЛВ.
7. Привести пример образования сложного высказывания из простых на примере какой-нибудь теоремы.
8. Записать следующие высказывания с помощью формул:
8.1. “Данное отношение есть отношение эквивалентности тогда и только тогда, когда оно рефлексивно, симметрично и транзитивно”;
8.2. “Если влажность так высока, то либо после полудня, либо вечером будет дождь”.
9. Даны атомарные высказывания: P 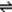 Ему нужен доктор, Q
Ему нужен доктор, Q 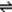 Ему нужен адвокат, R
Ему нужен адвокат, R 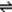 С ним произошел несчастный случай, S
С ним произошел несчастный случай, S  Он болен, U
Он болен, U  Он ранен. Записать в виде предложений русского языка следующие формулы:
Он ранен. Записать в виде предложений русского языка следующие формулы:
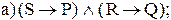
b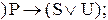
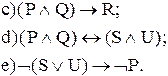
10. Для каждой из следующих формул определите, верно ли, что она общезначима, необщезначима, противоречива, непротиворечива или обладает некоторой комбинацией этих свойств:
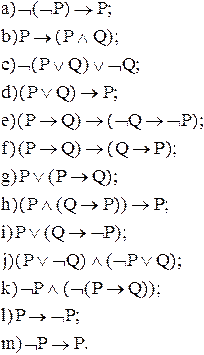
# Преобразование формул логики высказываний. Получение ДНФ, КНФ,
СДНФ, СКНФ. Способы задания булевых функций
Рассмотрим законы логики высказываний, доказательство истинности высказываний с помощью таблиц истинности, эквивалентные преобразования в логике высказываний, алгоритмы приведения произвольных формул логики высказываний к нормальным формам, а также правила записи СДНФ и СКНФ по таблицам истинности и способы задания булевых функций.
Часто бывает необходимо преобразовать формулы логики высказываний из одной формы в другую, особенно в так называемую “нормальную форму”. Это достигается путем эквивалентных преобразований формул. Говорят, что две формулы F и G эквивалентны или, что F эквивалентна G (обозначается F=G), тогда и только тогда, когда истинностные значения F и G совпадают при всех интерпретациях. Для осуществления эквивалентных преобразований произвольных формул логики высказываний используются следующие тождества (законы логики высказываний):
1) A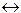 B=(A
B=(A B)Ù(B
B)Ù(B A);
A);
2) A B=ØAÚB;
B=ØAÚB;
3) законы коммутативности:
AÚB=BÚA, AÙB=BÙA;
4) законы ассоциативности:
(AÚB)ÚC=AÚ(BÚC),
(AÙB)ÙC=AÙ(BÙC);
5) законы дистрибутивности:
AÙ(BÚC)=(AÙB)Ú(AÙC),
AÚ(BÙC)=(AÚB)Ù(AÚC);
6) законы идемпотентности:
AÚA=A, AÙA=A;
7) законы элиминации:
AÚ(АÙB)=A, AÙ(AÚB)=A;
ØØA=A;
9) закон исключенного третьего:
AÚØA=U,
где U какая-либо общезначимая формула;
10) закон противоречия
AÙØA=Л,
11) тождества с константами
AÙЛ=Л, AÚЛ=A;
AÙU=A, AÚU=U;
12) законы де Моргана
Ø(AÚB)=ØAÙØB;
Ø(AÙB)=ØAÚØB;
Законы де Моргана обобщаются на случай n атомов:
Ø(A1ÚA2Ú...ÚAn) = ØA1ÙØA2Ù...ÙØAn
Ø(A1ÙA2Ù...ÙAn ) = ØA1ÚØA2Ú...ÚØAn.
Следует помнить, что в формулировке перечисленных эквивалентных соотношений (законов логики высказываний) переменные А,В, и т.д. обозначают не конкретные высказывания, а формулы. В указанные тождества можно подставлять любые формулы, и тождества будут справедливы. Указанные законы и тождества используются для эквивалентных преобразований формул с целью их упрощения или получения так называемых нормальных форм.
Литера есть атом или отрицание атома. Формула F находится в конъюнктивной нормальной форме (КНФ), если она имеет вид: F=F1ÙF2Ù...ÙFn, где каждая из F1, F2,..., Fn есть дизъюнкция литер. Формула F находится в дизъюнктивной нормальной форме (ДНФ), если она имеет вид: F=F1ÚF2Ú...ÚFn, где каждая из F1,F2,...,Fn есть конъюнкция литер. Всякая формула может быть преобразована в нормальную форму. Это легко достигается использованием законов ЛВ. Процедура преобразования формул в нормальные формы описывается следующим алгоритмом:
Шаг 1. Используем законы:
F 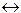 G=(F
G=(F G)Ù(G
G)Ù(G F),
F),
F  G=ØFÚG;
G=ØFÚG;
чтобы устранить (элиминировать) логические связки 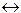 ,
,  .
.
Шаг 2. Несколько раз используем закон ØØF=F и законы де Моргана:
Ø(FÚG)=ØFÙØG,
Ø(FÙG)=ØFÚØG,
чтобы перенести знак отрицания непосредственно к атомам.
Шаг 3. Несколько раз используем дистрибутивные законы:
FÚ(GÙH)=(FÚG)Ù(FÚH),
FÙ(GÚH)=(FÙG)Ú(FÙH)
и другие законы, чтобы получить нормальную форму.
Наряду с задачей перехода от формулы высказывания к его таблице истинности зачастую требуется выполнить обратное: по заданной таблице истинности записать формулу которая передавала бы то же соответствие. Для этого используется совершенная дизъюнктивная нормальная форма (СДНФ) и совершенная конъюнктивная нормальная форма (СКНФ).
Конституента 1 - это конъюнкция, в которой по одному разу присутствуют литеры всех атомов, имеющихся в формуле. Свойства конституенты 1: 1) конституента 1 равна единице при единственной интерпретации, при которой и исходная формула также принимает единичное значение; 2) конъюнкция любого числа конституент 1 от одних и тех же переменных равна нулю. Конституента 0 - это дизъюнкция, в которую входят по одному разу литеры всех атомов, имеющихся в формуле. Свойства конституенты 0: 1) конституента 0 принимает нулевое значение при единственной интерпретации, при которой и исходная формула также равна нулю;
2) дизъюнкция любого числа конституент 0 равна 1.
СДНФ формулы G - это дизъюнкция всех ее конституент 1. СКНФ формулы G - это конъюнкция всех ее конституент нуля. Обозначим через 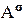 , где
, где 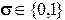 запись атома, взятого с отрицанием, либо без него, то есть: при s= 1
запись атома, взятого с отрицанием, либо без него, то есть: при s= 1 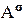 =A1=A; при s= 0
=A1=A; при s= 0 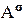 =A0=
=A0=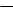 A. Справедливо следующее правило записи СДНФ по таблице истинности:
A. Справедливо следующее правило записи СДНФ по таблице истинности:
1) для каждой интерпретации, где формула равна единице, выписываем соответствующую конституенту единицы. В качестве показателей при атомах берем истинные значения атомов в данной интерпретации;
2) объединяем полученные значения конституенты единиц дизъюнкцией. Получаем СДНФ. Желательно выписывать конституенты 1 в порядке возрастания номеров соответствующих им интерпретаций.
Правило записи СКНФ по таблице истинности формулируется аналогично. Однако, на первом шаге, при формировании конституент в качестве показателей при атомах берут отрицания истинных значений атомов в соответствующей интерпретации.
Введенные ранее шесть таблиц истинности, полученные в результате использования логических связок 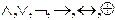 можно рассматривать как одноместные и двухместные функции особого вида. В них аргументы и значения могут принимать одно из двух возможных значений, обозначаемых 0 или 1. Такие функции называются логическими или булевыми.
можно рассматривать как одноместные и двухместные функции особого вида. В них аргументы и значения могут принимать одно из двух возможных значений, обозначаемых 0 или 1. Такие функции называются логическими или булевыми.
Функция вида f (x1,x2,...,xn)=y, где x1,x2,...,xn,у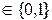 называется n-местной булевой функцией. Всего существует 4 одноместных булевых функций вида f i(x):
называется n-местной булевой функцией. Всего существует 4 одноместных булевых функций вида f i(x):
| X | f0(x) | f1(x) | f2(x) | f3(x) |
f 0(x)=0, f 1(x)=x, f 2(x)=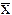 , f 3(x)=1.
, f 3(x)=1.
Всего существует 16 двухместных булевых функций вида j i(x,y):
| x y | j0 | j1 | j2 | j3 | j4 | j5 | j6 | j7 |
| 0 0 0 1 1 0 1 1 | ||||||||
| x y | j8 | j9 | j10 | j11 | j12 | j13 | j14 | j15 |
| 0 0 0 1 1 0 1 1 |
Наиболее известные булевы функции двух переменных:
j 1(x,y)=xÙy=x*y=xy=x&y;
j 6(x,y)=x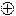 y ¾ сложение по mod 2 или функция неравнозначности;
y ¾ сложение по mod 2 или функция неравнозначности;
j 7(x,y)=хÚу ¾ дизъюнкция;
j 8(x,y)=х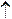 у=
у=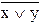 ¾ стрелка Пирса или отрицание дизъюнкции;
¾ стрелка Пирса или отрицание дизъюнкции;
j 9(x,y)=x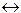 y ¾ эквиваленция или функция равнозначности;
y ¾ эквиваленция или функция равнозначности;
j 13(x,y)=х у=х
у=х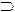 у ¾ импликация;
у ¾ импликация;
j 14(x,y)=х|y=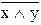 ¾ штрих Шеффера или отрицание конъюнкции;
¾ штрих Шеффера или отрицание конъюнкции;
Формула любого сложного высказывания может быть проинтерпретирована как булева функция, принимающая значение 1 на тех наборах значений аргументов (атомов в формуле ЛВ), при которых данное высказывание истинно, и принимающая значение 0 на тех наборах значений аргументов, на которых данное высказывание ложно. Любую булеву функцию можно задать таблицей истинности или с помощью СДНФ, СКНФ. Для булевых функций справедливы описанные выше тождества (законы алгебры логики) и правила перехода от таблиц истинности к СДНФ (СКНФ) и наоборот.
Рассмотрим примеры решения типичных упражнений и задач:
1. Получить ДНФ для формулы PÚ(ØQ) R.
R.
Решение. Воспользуемся алгоритмом приведения произвольной формулы ЛВ к нормальной форме:
Шаг 1. Избавляемся от операции импликации:
PÚ(ØQ) R=Ø(PÚ(ØQ))ÚR;
R=Ø(PÚ(ØQ))ÚR;
Шаг 2. Используя законы де Моргана, приближаем все отрицания непостредственно к атомам:
Ø(PÚ(ØQ))ÚR=(ØPÙØ(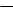 Q))ÚR;
Q))ÚR;
Шаг 3. Используем дистрибутивный закон, раскрываем скобки, используем закон двойного отрицания, приводим подобные члены, получаем ДНФ:
(ØPÙØ(ØQ))ÚR=(ØPÙQ)ÚR.
2. Получить КНФ для формулы (PÙ(QÚR)) S.
S.
Решение. Применяем тот же алгоритм.
Шаг 1. (PÙ(QÚR)) S=Ø(PÙ(ØQÚR))ÚS;
S=Ø(PÙ(ØQÚR))ÚS;
Шаг 2. Ø(PÙ(ØQÚR))ÚS=(ØPÚ(QÙØR))ÚS;
Шаг 3.(ØPÚ(QÙØR))ÚS=((ØPÚQ)Ù(ØPÚØR))ÚS=(ØPÚQÚS)Ù(ØPÚØRÚS).
3. Представить данную формулу в СКНФ: (PÚQ) ØR.
ØR.
Решение. (PÚQ) ØR=Ø(PÚQ)ÚØR=ØPÙØQÚØR=
ØR=Ø(PÚQ)ÚØR=ØPÙØQÚØR=
=(ØPÚØR)Ù(ØQÚØR)=(ØPÚØQÚØR)Ù(ØPÚQÚØR)Ù
Ù(ØPÚØQÚØR)Ù(PÚØQÚØR)=
=(ØPÚØQÚØR)Ù(ØPÚQÚØR)Ù(PÚØQÚØR).
4. По данной таблице истинности записать СДНФ и СКНФ формулы высказывания.
| A B C | F(A,B,C) |
| 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 |
Решение. Используем правило получения ДНФ по таблице истинности:
Шаг 1. Выписываем все конституенты 1 для каждой интерпретации, где F=1. В качестве показателей при атомах берем истинные значения атомов в данной интерпретации. Получаем следующие конституенты 1:
A0ÙB1ÙC0=ØAÙBÙØC, A1ÙB0ÙC0=AÙØBÙØC, A1ÙB1ÙC0=AÙBÙØC
Шаг 2. Соединяя полученные конституенты 1 дизъюнкциями, получаем СДНФ:
(ØAÙBÙØC)Ú(AÙØBÙØC)Ú(AÙBÙØC)=F.
Теперь получим представление той же формулы ЛВ в виде СКНФ:
Шаг 1. Выписываем все конституентны 0 для каждой интерпретации, где F=0. В качестве показателей при атомах берем отрицания значений атомов в данной интерпретации. Получаем следующие конституенты 0:
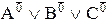 =A1ÚB1ÚC1=AÚBÚC,
=A1ÚB1ÚC1=AÚBÚC,
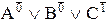 =A1ÚB1ÚC0=AÚBÚØC,
=A1ÚB1ÚC0=AÚBÚØC,
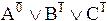 =A1ÚB0ÚC0=AÚØBÚØC,
=A1ÚB0ÚC0=AÚØBÚØC,
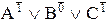 =A0ÚB1ÚC0=ØAÚBÚØC,
=A0ÚB1ÚC0=ØAÚBÚØC,
Шаг 2. Соединяя полученные конституенты 0 конъюнкциями, получаем СКНФ: (AÚBÚC)Ù(AÚBÚØC)Ù(AÚØBÚØC)Ù(ØAÚBÚØC).
Контрольные вопросы и задания по теме:
1. Эквивалентные соотношения в логике высказываний.
2. Законы ЛВ.
3. Конституенты единицы. Конституенты нуля.
4. ДНФ, СДНФ, КНФ, СКНФ.
5. Булевы функции. Способы задания булевых функций.
6. Проверьте эквивалентность следующих формул, преобразуя формулы с обеих сторон от знака = к одной и той же нормальной форме:
а)PÙP=P, PÚP=P
b)(P Q)Ù(P
Q)Ù(P R)=(P
R)=(P (QÙR)),
(QÙR)),
c)(PQ) (PÙQ)=(ØP
(PÙQ)=(ØP Q)Ù(P
Q)Ù(P Q),
Q),
d)PÙQÙ(ØPÚØQ)=ØPÙØQÙ(PÚQ),
e)PÚ(P (PÙQ))=ØPÚØQÚ(PÙQ)
(PÙQ))=ØPÚØQÚ(PÙQ)
7. Определить, являются ли следующие формулы высказываний общезначимыми, противоречивыми или выполнимыми:
a)(X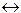 Y)
Y)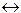 (X
(X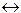 (Y
(Y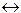 X)),
X)),
b)X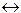 (XÚY),
(XÚY),
c)(X Y)
Y) ((Y
((Y Z)
Z) (X
(X Z))
Z))
8. Перейти от формулы 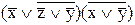 булевой функции к ее СДНФ.
булевой функции к ее СДНФ.
9. Перейти от формулы 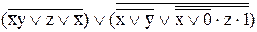 к таблице булевой функции через СДНФ и СКНФ.
к таблице булевой функции через СДНФ и СКНФ.
 2014-02-09
2014-02-09 3752
3752