Общее уравнение плоскости может быть полным или неполным, т.е. в нем могут отсутствовать одно или несколько слагаемых. Вид уравнения определяет ориентацию плоскости в пространстве. Для построения плоскости лучше использовать уравнение “в отрезках”. Исследование общего уравнения плоскости представлено в таблице.
| Вид уравнения | Геометрическая иллюстрация | Вид уравнения | Геометрическая иллюстрация |
Ax + By + Cz + D = 0 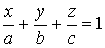 | 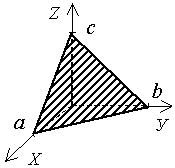 плоскость пересекает оси OX, OY, OZ плоскость пересекает оси OX, OY, OZ | Ax + By + Cz = 0 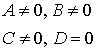 | 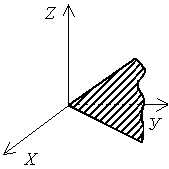 плоскость проходит через начало координат плоскость проходит через начало координат |
Ax + By + D = 0 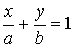 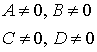 | 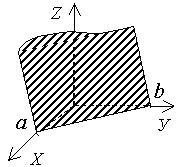 плоскость e e оси OZ плоскость e e оси OZ | Ax + By + D = 0 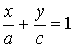 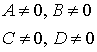 | 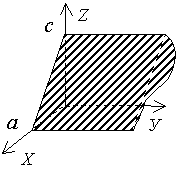 плоскость e e оси OУ плоскость e e оси OУ |
By + Cz + D = 0 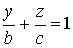 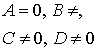 | 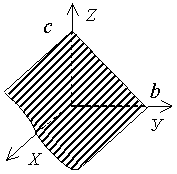 плоскость e e оси OХ плоскость e e оси OХ | Ax + D = 0 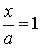 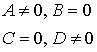 | 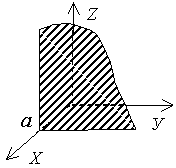 плоскость e e плоскости ZOY плоскость e e плоскости ZOY |
By + D = 0 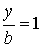 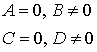 | 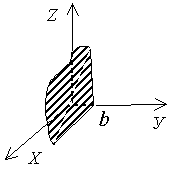 плоскость e e плоскости XOZ плоскость e e плоскости XOZ | Cz + D = 0 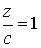 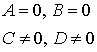 | 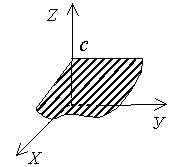 плоскость e e плоскости XOУ плоскость e e плоскости XOУ |
Ax = 0 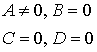 | 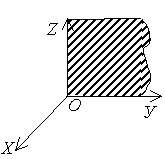 плоскость ZOY плоскость ZOY | By = 0 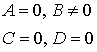 Cz = 0 Cz = 0 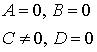 | 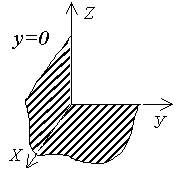 |
Задача. Построить следующие плоскости: 1) 4 x + z - 8 = 0;
2) 6 x - 2 y + z = 0;
3) z - 5 = 0.
Решение. 1) 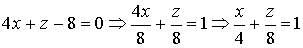 , т.е. a = 4, c = 8. Плоскость 4 x + z - 8 = 0 параллельна оси ОУ. 2) Плоскость 6 x - 2 y + z = 0 проходит через начало координат, так как свободный член D = 0. Найдем уравнение прямой, по которой данная плоскость пересекается с плоскостью ХОУ , т.е. a = 4, c = 8. Плоскость 4 x + z - 8 = 0 параллельна оси ОУ. 2) Плоскость 6 x - 2 y + z = 0 проходит через начало координат, так как свободный член D = 0. Найдем уравнение прямой, по которой данная плоскость пересекается с плоскостью ХОУ | 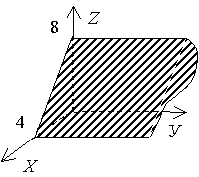 |
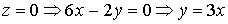 . Найдем уравнение прямой, по которой данная плоскость пересекается с плоскостью YOZ: . Найдем уравнение прямой, по которой данная плоскость пересекается с плоскостью YOZ: 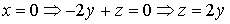 . 3) . 3) 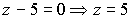 . Данная плоскость параллельна плоскости XOY . Данная плоскость параллельна плоскости XOY | 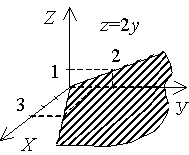 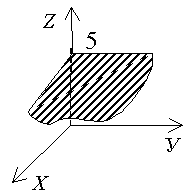 |
| В ы в о д ы: 1. Если в уравнении плоскости отсутствует свободный член, то плоскость проходит через начало координат. 2. Если в уравнении плоскости отсутствует одна координата, то плоскость параллельна оси отсутствующей координаты. 3. Если в уравнении плоскости отсутствуют две координаты, то плоскость параллельна координатной плоскости отсутствующей координаты. 4. Если в уравнении плоскости отсутствуют две координаты и свободный член, то это есть координатная плоскость отсутствующей координаты. | |
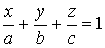
 плоскость пересекает оси OX, OY, OZ
плоскость пересекает оси OX, OY, OZ 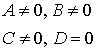
 плоскость проходит через начало координат
плоскость проходит через начало координат 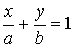
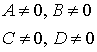
 плоскость e e оси OZ
плоскость e e оси OZ 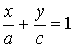
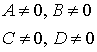
 плоскость e e оси OУ
плоскость e e оси OУ 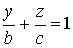
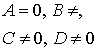
 плоскость e e оси OХ
плоскость e e оси OХ 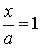
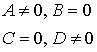
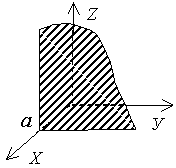 плоскость e e плоскости ZOY
плоскость e e плоскости ZOY 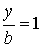
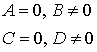
 плоскость e e плоскости XOZ
плоскость e e плоскости XOZ 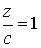
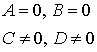
 плоскость e e плоскости XOУ
плоскость e e плоскости XOУ 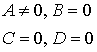
 плоскость ZOY
плоскость ZOY 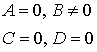 Cz = 0
Cz = 0 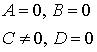
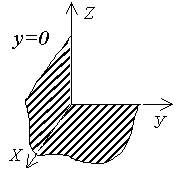
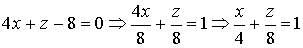 , т.е. a = 4, c = 8. Плоскость 4 x + z - 8 = 0 параллельна оси ОУ. 2) Плоскость 6 x - 2 y + z = 0 проходит через начало координат, так как свободный член D = 0. Найдем уравнение прямой, по которой данная плоскость пересекается с плоскостью ХОУ
, т.е. a = 4, c = 8. Плоскость 4 x + z - 8 = 0 параллельна оси ОУ. 2) Плоскость 6 x - 2 y + z = 0 проходит через начало координат, так как свободный член D = 0. Найдем уравнение прямой, по которой данная плоскость пересекается с плоскостью ХОУ 
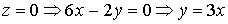 . Найдем уравнение прямой, по которой данная плоскость пересекается с плоскостью YOZ:
. Найдем уравнение прямой, по которой данная плоскость пересекается с плоскостью YOZ: 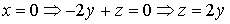 . 3)
. 3) 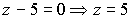 . Данная плоскость параллельна плоскости XOY
. Данная плоскость параллельна плоскости XOY 

 2014-02-09
2014-02-09 4008
4008
