«Классическое»определение вероятности предполагает, что число исходов испытанеий конечно. На практике же часто встречаются испытания,число возможных исходов бесконечно.. В таких случаях классическое определение неприемлемо.
Наиболее слабая сторона этого определения состоит в том, что очень невозможно представить результат испытания в виде совокупности элементарных событий. Еще труднее указать основания, позволяющие считать элементарные события равновозможными.
По этим причинам наряду с классическим определением пользуются также статистическим определением вероятности, принимая за вероятность события относительную частоту или число близкое к ней. Например, если в результате достаточно большого числа испытаний оказалось, что относительная частота весьма близка к числу 0,4, то это число можно принять за статистическую вероятность события.
Пример. В ящике имеется 50 одинаковых деталей, 5 из которых окрашены. Найти вероятность того, что наудачу извлеченная деталь окажется окрашенной.
Решение. Вычислим частоту события, состоящего в том, что деталь окрашена. В данном случае, она является статистической вероятностью
Р(А) = 5/50=0,1.
Геометрическое определение вероятности используется при вычислении вероятности появления события в том случае, когда результат испытания определяется случайным положением точек в некоторой области, причем любые положения точек в этой области равновозможны. Если размер этой области S, а размер той части области, попадание в которую благоприятстсвует данному событию есть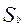 , то вероятность события А равна
, то вероятность события А равна
Р(А)=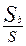 . v
. v
Область S может иметь любое число измерений, поэтому 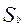 и S могут представлять собой длины отрезков, площади, объемы и т.д.
и S могут представлять собой длины отрезков, площади, объемы и т.д.
При решении задач на геометрические вероятности особое внимание следует обращать на то, какие параметры принимают равновозможные значения.
Пример. На квадрат со стороной а наудачу брошена точка. Найти вероятность того, что точка окажется внутри круга, вписанного в данный квадрат
Решение. Площадь квадрата со стороной а составляет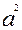 , площадь круга, вписанного в квадрат есть
, площадь круга, вписанного в квадрат есть 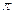
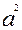 . Таким образом, вероятность в нашем случае равна р(А)=
. Таким образом, вероятность в нашем случае равна р(А)=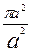 =
=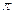 .
.
 2014-02-12
2014-02-12 1733
1733