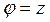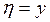
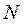
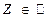
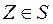
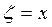
Расширенная комплексная плоскость

Отождествим плоскость 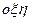с комплексной плоскостью 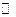, совместив соответственно ос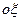и 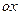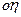и , и 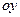. Рассмотрим в системе координат 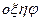трёхмерную сферу Римана с центром в точке 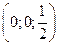радиуса 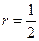. Имеем 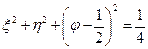- уравнение сферы Римана .

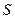Точку 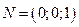назовём северным полюсом сферы Римана .

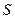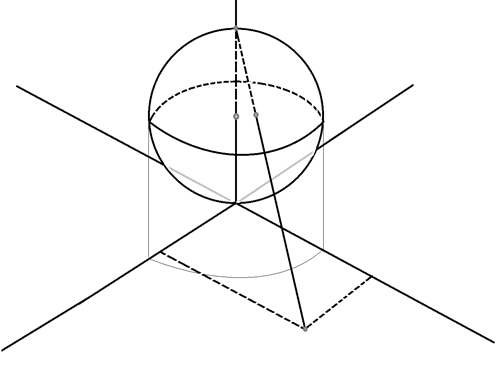
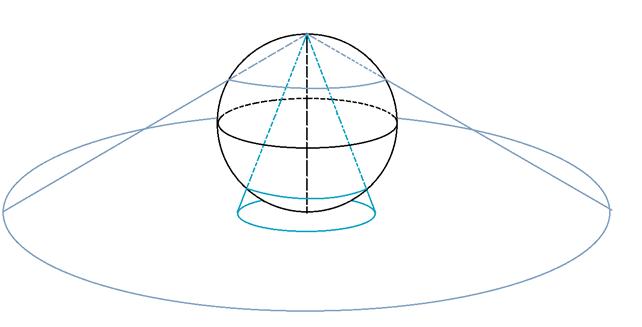
Определение. Рассмотрим соответствие 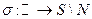, которое каждому комплексному числу 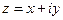ставит в соответствие число 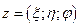на сфере Римана, которое является пересечением луча 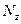с 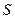(т. е. луча, соединяющего точк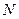и и ).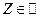

Определение. Введем бесконечно удаленную точку (бесконечность) 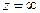, соответствующую северному полюсу 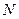при стереографической проекции .

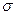Видим, что внешняя часть кругов бесконечного радиуса на 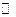соответствует всего одной точке .

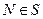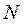
Обозначим 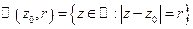. Геометрическая интерпретация – окружность с центром в точке 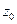радиуса .

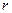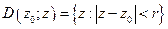- открытый круг

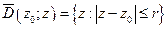- замкнутый круг

Определение. 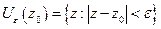- -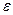окрестность точки .

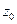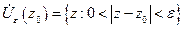- проколотая 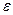-окрестность точки .

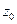Определение. Точка 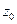называется внутренней точкой множества 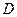, если найдется 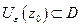(«Целиком лежащая» в ).

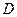Точка 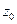называется предельной точкой множества 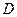, если в любой её проколотой окрестности лежат точки множества .

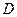Точка 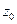называется граничной точкой множества 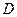, если в любой её окрестности лежат точки, как принадлежащие, так и не принадлежащие .

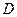Совокупность всех граничных точек множества 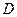называется границей множества 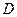и обозначается .

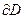Множество называется открытым, если все его точки внутренние.

Множество называется замкнутым, если содержит все свои предельные точки.

Замыканием множества 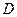называется множество 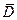, содержащее все точки множества 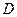и все его предельные точки.

Упражнение. Доказать, что граница любого множества является замкнутым множеством.

Доказательство: Граница – замкнутая линия; 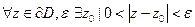(замкнутость даёт наличие точки-соседа для любой окрестности любой точки границы). Видим, что все точки предельны, все содержатся в 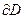, значит, любая граница – замкнутое множество.

Определение. Множество на комплексной плоскости называется связным, если любые его 2 точки можно соединить непрерывной кривой, не выходящей за пределы множества.

Связное открытое множество называется областью.