2014-02-12
802
Считаем, что встречающиеся здесь подынтегральные функции интегрируемы.
1. 
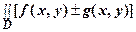dx dy = 
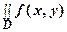dx dy ± 
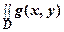dx dy.
2. 
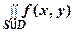dx dy = 
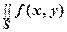dx dy ± 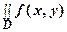dx dy.
3. 
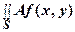dx dy = A 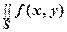dx dy.
4. Если для всех точек (x, y)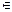
D f (x, y) ≤ g (x, y), то 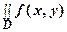dx dy ≤ 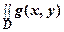dx dy.
5. Площадь плоской области: 
= S, т.к. 
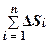= S.
6. Если f (x, y) непрерывна в замкнутой областиD, площадь которой S, то
mS ≤ 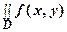dx dy ≤ MS, где m и M - соответственно наименьшее и наибольшее
значения f (x, y) в областиD.
7. Теорема о среднем значении функции. Если f (x, y) непрерывна в замкнутой
областиD, площадь которой S, то в этой области существует такая точка (х 0, у 0), что 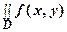dx dy = f (х 0, у 0) · S.
Величину f (х 0, у 0) =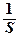 
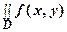dx dy называют средним значением функцииf ( x, y )
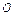
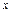
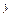
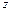
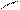
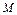
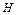в областиD.
Геометрический смысл теоремы о среднем значении. Если в области D
функция f (x, y) ³ 0, то данная теорема гласит, что существует прямой
цилиндр с основанием D (площадь которого равна S) и высотой
H = f (x 0, y 0), объем которого равен объему цилиндрического тела (рис. 4).
 |
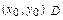Рис. 4.
