Рассмотрим 2-х мерное квазилинейное однородное уравнение, котором коэффициенты при производных являются функциям х и у
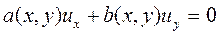 . (11.11)
. (11.11)
Введем новые переменные
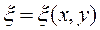 и
и 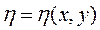 . (11.12)
. (11.12)
и новую функцию
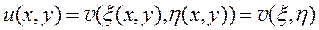 (11.13)
(11.13)
Продифференцировав функцию (11.13) по х и у, получим
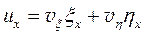 и
и 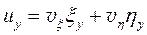 (11.14)
(11.14)
Подставив (11.14) в (11.11), получим
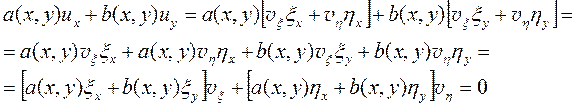
Предположим, что коэффициент 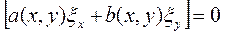 , тогда получим, что
, тогда получим, что 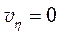 и решение этого уравнения по алгоритму, рассмотренному ранее при решении уравнения (11.4) принимает вид
и решение этого уравнения по алгоритму, рассмотренному ранее при решении уравнения (11.4) принимает вид
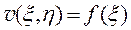 , (11.15)
, (11.15)
но вид переменной ξ нам неизвестен и как, же ее найти? Рассмотрим систему обыкновенных дифференциальных уравнений
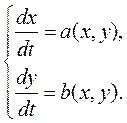 (11.16)
(11.16)
Для любого решения x (t), y (t) этой системы функция
F [ x (t), y (t)] = const,
Называется общим интегралом этой системы (11.16) и, если F = const, то производная от нее равна нулю 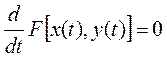 или раскрывая эту производную, получим
или раскрывая эту производную, получим
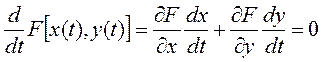 , (11.17)
, (11.17)
Исходя из того, что в системе (11.16) - 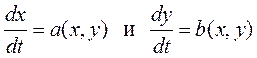 , то уравнение (11.17) можно записать в виде
, то уравнение (11.17) можно записать в виде
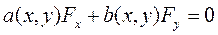 (11.18)
(11.18)
Анализируя уравнение (11.18) мы видим, что оно совпадает с исходным уравнением (11.11), следовательно, решениями уравнения (11.11) являются первые интегралы системы (11.16). Записав симметричную форму системы (11.16)
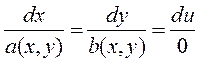 , (11.19)
, (11.19)
Эти уравнения называются уравнениями характеристик. Найдем интегралы этой системы. Первый интеграл очевиден
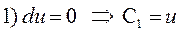 .
.
Второй интеграл найдем из следующей комбинации
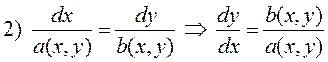 ,
,
интегрируя это уравнение, найдем
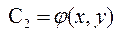 .
.
Таким образом, общий интеграл уравнения (11.11) можно представить в виде
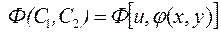 , (11.20)
, (11.20)
а общее решение будет выглядеть как
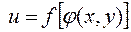 . (17.21)
. (17.21)
Интегралы С 1 и С 2 уравнения (11.19) называются характеристиками.
Пример 11.1. Найти общий интеграл и общее решение уравнения
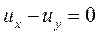
▲ Запишем для этого уравнения систему (11.16)
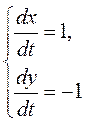
Далее запишем симметричную форму этой системы
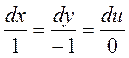 .
.
Первый интеграл очевиден
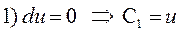 .
.
Второй интеграл найдем из следующей комбинации
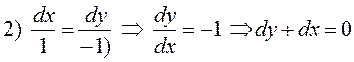 ,
,
интегрируя это уравнение, найдем
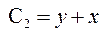 .
.
Таким образом, общий интеграл исходного уравнения можно представить в виде
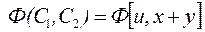 ,
,
а общее решение будет выглядеть как
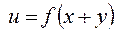 .
.
Аналогичным образом решается уравнение
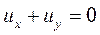
и его решение имеет вид
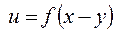 .▲
.▲
Неоднородные уравнения решаются аналогичным образом.
Пример 11.2. Найти общий интеграл и общее решение уравнения 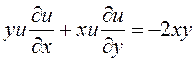 .
.
▲ Запишем для него систему (11.16)
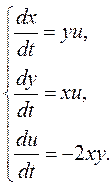
Далее запишем симметричную форму этой системы
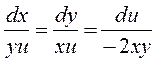 .
.
Первый интеграл очевиден
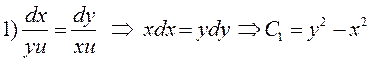 .
.
Второй интеграл найдем из следующей комбинации
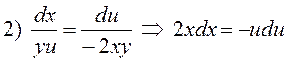 ,
,
интегрируя это уравнение, найдем
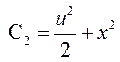 .
.
Таким образом, общий интеграл исходного уравнения можно представить в виде
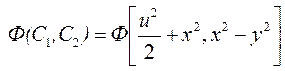 ,
,
а общее решение будет выглядеть как
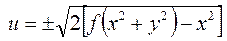 . ▲
. ▲
 2014-02-12
2014-02-12 905
905







