Если существует дифференцируемая функция
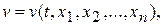
называемая функцией Ляпунова, удовлетворяющая в окрестности точки х =0 следующим условиям:
1) 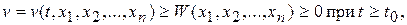 где непрерывная функция W имеет строгий минимум в точке х =0, причем
где непрерывная функция W имеет строгий минимум в точке х =0, причем 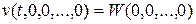 ;
;
2) полная производная
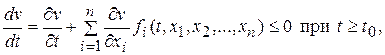
то тривиальное решение 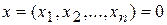 устойчиво.
устойчиво.
Если же вместо условия 2) выполняется неравенство
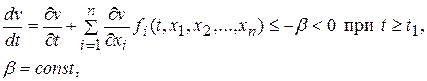
то тривиальное решение асимптотически устойчиво.
Пример 10.1. Определить является ли устойчивым решение системы:
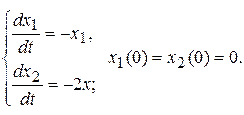
▲ Очевидно, нужно исследовать на устойчивость нулевое решение системы 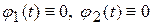 . Интегрируя исходную систему, получаем
. Интегрируя исходную систему, получаем
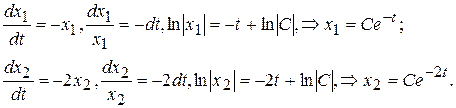
Пусть 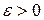 задано. Найдем
задано. Найдем 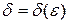 такое, что из неравенства (10.4)
такое, что из неравенства (10.4)
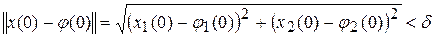
следует неравенство (10.5)
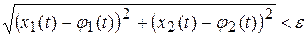
для каждого t >0 одновременно. Поскольку из неравенства
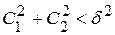
следует
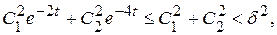
то при t >0 для произвольного 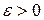 , полагая
, полагая 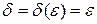 , получаем
, получаем
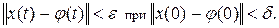
Таким образом, тривиальное решение исходной системы является устойчивым по Ляпунову. Более того, так как
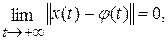
то это решение устойчиво асимптотически. ▲
Пример 10.2. Определить является ли устойчивым нулевое решение системы, если известно, что общее решение системы имеет вид:
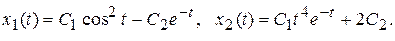
▲ Пусть 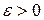 задано, t 0 – произвольный момент времени. По заданному
задано, t 0 – произвольный момент времени. По заданному 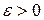 найдем
найдем 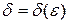 >0 такое, что из неравенства
>0 такое, что из неравенства
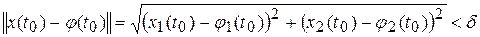
вытекало бы неравенство
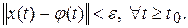
Положив для простоты t 0=0, имеем:
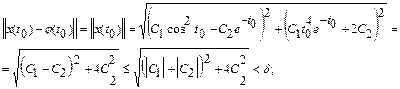 (П10.2.1)
(П10.2.1)
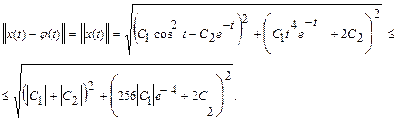 (П10.2.1)
(П10.2.1)
Но, как следует из (П10.2.1), 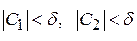 , поэтому оценку (П10.2.2) можно продолжить следующим образом:
, поэтому оценку (П10.2.2) можно продолжить следующим образом:
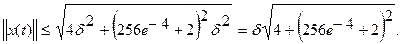
Отсюда следует, что если возьмем
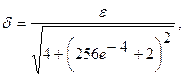
то получим неравенство 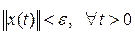 одновременно. Таким образом, согласно определению, нулевое решение устойчиво по Ляпунову. ▲
одновременно. Таким образом, согласно определению, нулевое решение устойчиво по Ляпунову. ▲
Пример 10.3. Исследовать на устойчивость по первому приближению решение системы
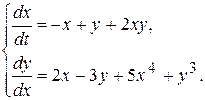
▲ Приведем эту систему к виду (10.18)
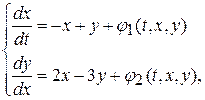
где
 .
.
Покажем, что функции  удовлетворяют неравенству (10.20):
удовлетворяют неравенству (10.20):
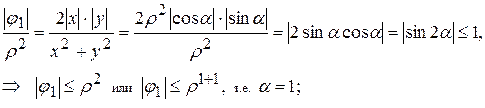
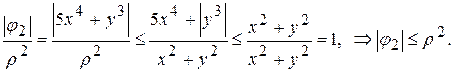
В этих выкладках 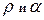 означают полярные координаты точки (х,у).
означают полярные координаты точки (х,у).
Таким образом, функции  удовлетворяют неравенству (10.20). Поэтому выделим из исходной системы линейную часть с постоянными коэффициентами:
удовлетворяют неравенству (10.20). Поэтому выделим из исходной системы линейную часть с постоянными коэффициентами:
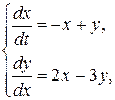 (П10.3.1)
(П10.3.1)
и составив характеристическое уравнение
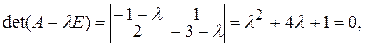
найдем его корни
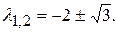
Оба корня являются отрицательными, следовательно, тривиальное решение линейной системы (П10.3.1) асимптотически устойчиво. Исходя из этого решение исходной системы также будет асимптотически устойчивым. ▲
Пример 10.4. Исследовать на устойчивость по первому приближению решение системы
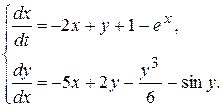
▲ Приведем эту систему к виду (10.18)
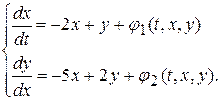
где
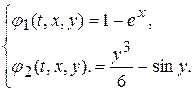
Разложим функции 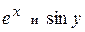 по формуле Маклорена
по формуле Маклорена
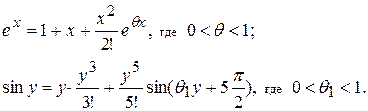
Следовательно,
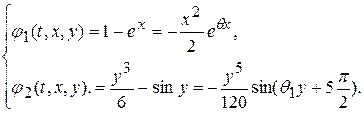
Ограничимся рассмотрением точек (x,y), удовлетворяющих неравенству 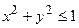 , т.е. принадлежащих кругу с центром в начале координат и радиусом, равным единице. Тогда будем иметь:
, т.е. принадлежащих кругу с центром в начале координат и радиусом, равным единице. Тогда будем иметь:
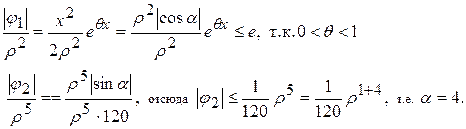
Таким образом, функции  удовлетворяют неравенству (10.20). Поэтому выделим из исходной системы линейную часть с постоянными коэффициентами:
удовлетворяют неравенству (10.20). Поэтому выделим из исходной системы линейную часть с постоянными коэффициентами:
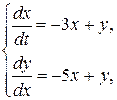 (П10.4.1)
(П10.4.1)
и составив характеристическое уравнение
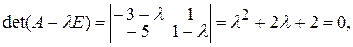
найдем его корни
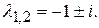
Корни являются комплексно сопряженными, имеющими отрицательные действительные части, следовательно, тривиальное решение линейной системы (П10.4.1) асимптотически устойчиво. Исходя из этого, решение исходной системы будет устойчивым. ▲
Пример 10.5. Исследовать на устойчивость нулевое решение уравнения
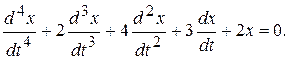
▲ Для исследования на устойчивость нулевого решения построим матрицу Гурвица
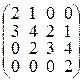 .
.
Определим, положительны или отрицательны ее главные миноры
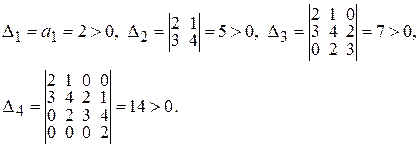
Поскольку главные миноры матрицы Гурвица положительны, то из этого следует, что действительные части корней характеристического уравнения
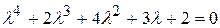 ,
,
соответствующего исходному уравнению, будут отрицательными, а из этого следует, что нулевое решение исходного уравнения является асимптотически устойчивым. ▲
Пример 10.6. Исследовать на устойчивость нулевое решение уравнения
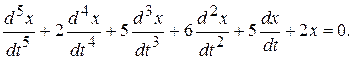
▲ Для исследования на устойчивость нулевого решения построим матрицу Гурвица
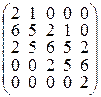
Определим, положительны или отрицательны ее главные миноры
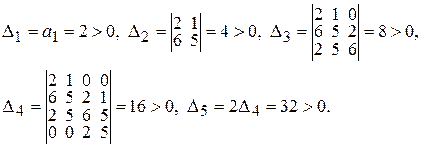
Поскольку главные миноры матрицы Гурвица положительны, то из этого следует, что действительные части корней характеристического уравнения
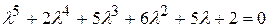 ,
,
соответствующего исходному уравнению, будут отрицательными, а из этого следует, что нулевое решение исходного уравнения является асимптотически устойчивым. ▲
Пример 10.7. Построив функцию Ляпунова, исследовать на устойчивость решение системы
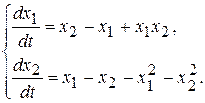
▲ В качестве функции Ляпунова выберем функцию
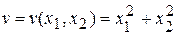
и проверим, удовлетворяет она условиям
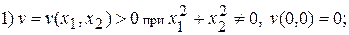
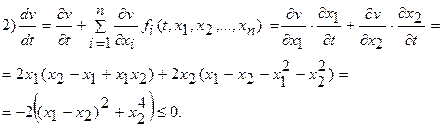
Следовательно, можно утверждать, что нулевое решение 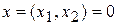 устойчиво. Более того, при вычислении производной функции Ляпунова мы получили поверхность
устойчиво. Более того, при вычислении производной функции Ляпунова мы получили поверхность
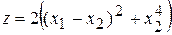 ,
,
имеющую чашеобразный вид. Поэтому существует достаточно малая окрестность 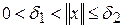 такая, что
такая, что 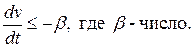 Следовательно, в данном случае нулевое решение будет устойчиво асимптотически. ▲
Следовательно, в данном случае нулевое решение будет устойчиво асимптотически. ▲
Пример 10.8. Построив функцию Ляпунова, исследовать на устойчивость решение системы
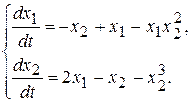
▲ В качестве функции Ляпунова выберем функцию
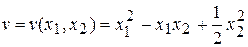
и проверим, удовлетворяет она условиям
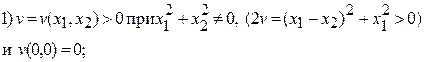
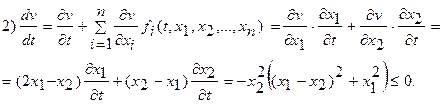
Следовательно, можно утверждать, что нулевое решение 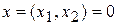 устойчиво. ▲
устойчиво. ▲
Пример 10.9. Построив функцию Ляпунова, исследовать на устойчивость решение системы
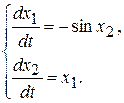
▲ В качестве функции Ляпунова выберем функцию
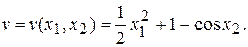
Очевидно, в некоторой малой окрестности точки (0,0), исключая саму эту точку будет v >0. Далее, полная производная имеет вид:
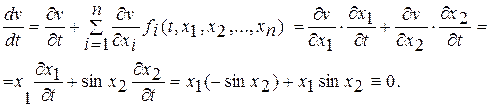
Следовательно, нулевое решение 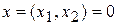 устойчиво. ▲
устойчиво. ▲
Пример 10.10. Построив функцию Ляпунова, исследовать на устойчивость решение системы
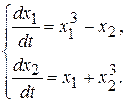
▲ В качестве функции Ляпунова выберем функцию
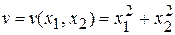
и проверим, удовлетворяет она условиям
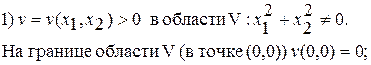
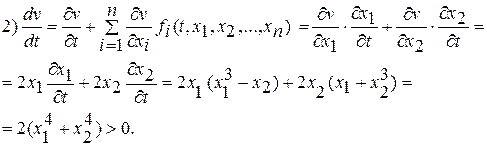
Следовательно, в силу того, что условие 2) не выполнено, нулевое решение 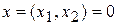 будет неустойчиво. ▲
будет неустойчиво. ▲
 2014-02-12
2014-02-12 7805
7805
