3073
Лекция 11. УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА
Часть 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ
Задания для самостоятельной работы
Исследовать на устойчивость решения систем
10.1.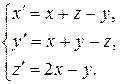 
10.2.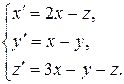 
10.3.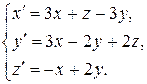 
10.4.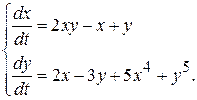 
10.5.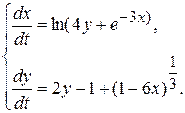 
10.6.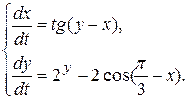 
10.7.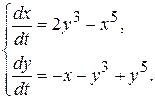 
10.8.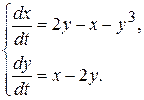 
10.9.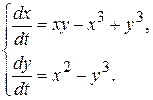 
10.11.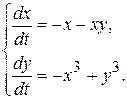 
Рассмотрим уравнение вида
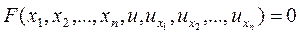, (11.1)
в котором х1, х2, …, хn - независимые переменные функции u;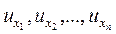 
- частные производные функции u по переменным х1, х2, …, хn .
Уравнение (11.1) называется уравнением в частных производных 1-го порядка. При этом, если уравнение (11.1) имеет вид
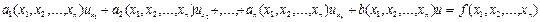,(11.2)
то оно будет называться линейным уравнением, а если уравнение (11.1) линейно только относительно частных производных и имеет вид
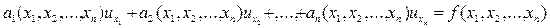,(11.3)
то оно будет называться квазилинейным уравнением. Уравнения (11.2) и (11.3) также называются «n»-мерными неоднородными уравнениями, если функции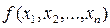 
в этих уравнениях будут равны нулю, то тогда они будут называться однородными уравнениями. Таким образом, «мерность» уравнения определяется количеством независимых переменных х1, х2, …, хn.
Рассмотрим 2-х мерное квазилинейное однородное уравнение
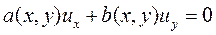, (11.4)
в котором для всех х и у выполняется неравенство
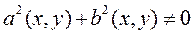. (11.5)
Пусть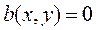 
, тогда уравнение (11.4) принимает вид
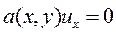, (11.6)
Тогда по условию (17.5) коэффициент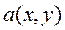 
, в силу того, что 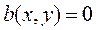, не может быть равен нулю, следовательно, может выполнятся только
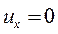или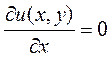 
(11.7)
В уравнениях (11.7) переменная у присутствует лишь в качестве параметра. Зафиксируем ее значение, например, у = у1, тогда функция u1(x) = u(x,y1) и уравнением (7) принимает вид
.
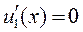Решением этого уравнения будет функция
.
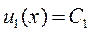Далее продолжим, зафиксируем у = у2, тогда функция u2(x) = u(x,y2) и уравнением (7) принимает вид
.
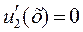Решением этого уравнения будет функция
.
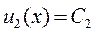Продолжая далее, получим для у = уn,
.
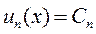Константы С1, С2, …, Сn между собой никак не связаны. Мы видим, что они связаны лишь с переменной у и, если охватить все возможные значения константы, то решение уравнения (11.7) необходимо записать в виде
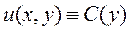. (11.8)
Если предположить, что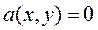 
, тогда уравнение (11.4) принимает вид
,
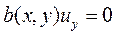и по условию (11.5) коэффициент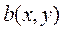 
, в силу того, что 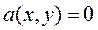, не может быть равен нулю, следовательно, может выполнятся только
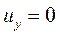или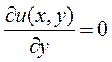 
(11.9)
Далее поступая точно также, как мы поступали выше, только фиксируя значения х, получим х = х1, тогда функция u1(у) = u(у,х1) и уравнением (11.7) принимает вид
.
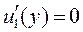Решением этого уравнения будет функция
.
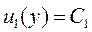Далее продолжим, зафиксируем х = х2, тогда функция u2(х) = u(у,х2) и уравнением (17.7) принимает вид
.
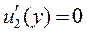Решением этого уравнения будет функция
.
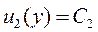Продолжая далее, получим для х = хn,
.
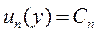Константы С1, С2, …, Сn между собой никак не связаны. Мы видим, что они связаны лишь с переменной х и, если охватить все возможные значения константы, то решение уравнения (11.7) необходимо записать в виде
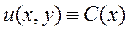. (11.10)
