Обобщающие характеристики центра распределения и степени вариации не дают представления о форме распределения, так как не вскрывают характера изменения частот.
Для выражения особенностей формы распределения применяются ранговые характеристики.
Ранговые характеристики – это варианты, занимающие в вариационном ряду определенное место.
К их числу относятся квартили, децили, перцентили.
Квартили – значения признака, которые делят ранжированный ряд на 4 равные по численности части.
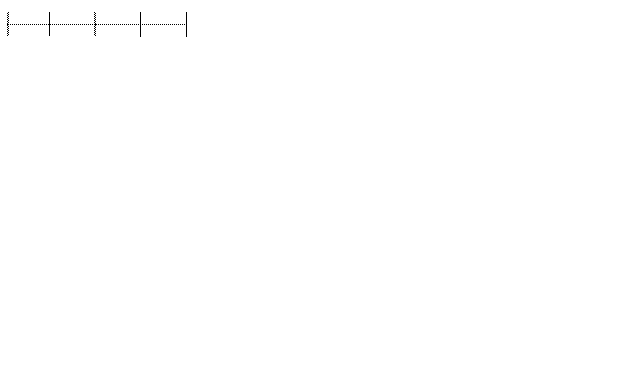 Q1 Q2 Q3
Q1 Q2 Q3
Первая квартиль – Q1
Вторая квартиль (совпадает с медианой) - Q2
Третья квартиль - Q3
Вычисление квартилей аналогично вычислению медианы: сначала определяют положение (место) квартили в ряду.
Место первой квартили: 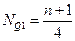
Место второй квартили: 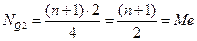
Место третьей квартили: 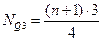
Затем по накопленным частотам определяют численное значение по формуле:
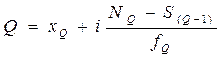
где xQ – нижняя граница интервала, в котором находится квартиль
NQ – место квартили
S(Q-1) – накопленная частота интервала, предшествующего тому, где находится квартиль
fQ – частота интервала, в котором находится квартиль
Децили – значения признака, которые ранжированный ряд делят на 10 равных частей. Расчеты ведутся аналогично расчетам квартилей:
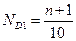 и так далее до
и так далее до 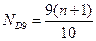 , где n – общее число единиц в совокупности
, где n – общее число единиц в совокупности
Численное значение определяется по формуле:
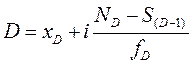
где xD – нижняя граница интервала, в котором находится дециль
ND – место децили
S(D-1) – накопленная частота интервала, предшествующего тому, где находится дециль
fD – частота интервала, в котором находится дециль
Перцентили – значения признака, делящие ранжированный ряд на 100 равных частей. Все вычисления аналогичны вычислениям децилей и квартилей.
Предварительная оценка рассеяния признака определяется с помощью размаха вариации: 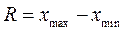
Но, если критические значения признака не типичны для совокупности, то есть они являются аномальными значениями, то используют квартильный, децильный и перцентильный размах.
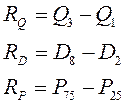 Квартильный размах:
Квартильный размах:
Децильный размах:
Перцентильный размах:
С точки зрения применения для различных шкал:
а) коэффициент вариации вычисляется и имеет смысл только для шкал равных отношений
б) медиана рассчитывается только для порядковых шкал
в) Мода – только для номинальных шкал
г) Средняя арифметическая – для интервальных и шкал равных отношений
д) Все показатели вариации вычисляются только для интервальных шкал или шкал равных отношений.
 2014-02-12
2014-02-12 12005
12005








