Основные определения. Случайные события и вероятности

Случайные события и вероятности

· Событие А, В,…– любая качественная характеристика результата опыта.

· Случайное событие – то, которое в результате опыта может произойти, а может и не произойти.

· Достоверное событие – то, которое обязательно появляется в результате опыта.

· Невозможное событие – то, которое не может появиться в результате опыта.

· Событие А влечет за собой событие В (А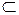В) – если при совершении события А событие В обязательно совершается.

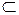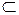· Эквивалентные события А = В, если АВ и ВА.

· Противоположные события – если совершение одного влечет несовершение другого и наоборот.

· Несовместные события – такие два события, совместное осуществление которых – событие невозможное.

· Совместные события – те, которые не являются несовместными. Не обязательно появляется вместе.

· Группа событий – совокупность нескольких событий, которые могут появиться в данном опыте.

· Полная группа событий – если хотя бы одно из событий, входящих в группу, обязательно совершается. Таким образом, противоположные события – это два несовместных события, образующих полную группу.

· Случаи – несовместные и равновозможные события, составляющие полную группу.

· Случай благоприятствует событию А, если он влечет за собой событие А.

· Случай неблагоприятствует событию А, если он не влечет за собой события А.

· Сумма событий В = А₁+А₂+… - это событие, эквивалентное совершению хотя бы одного из слагаемых событий.

· Произведение событий В = А₁А₂… - это событие, эквивалентное совместному совершению перемножаемых событий.

· Операции над событиями удовлетворяют свойствам ассоциативности, дистрибутивности и коммутативности, т.е. возможно объединение в скобки и перестановки любых слагаемых или сомножителей.

· Отметим: А+А = А; АА = А.

· Операции деления событий и умножения их на число не введены, поэтому не имеют смысла выражения вида А/В, 2А, 3А+4В и т.д.

· Геометрическая интерпретация событий и операций над ними.

· Частота события m / n. Серии из n опытов дают разные величины m.

· Устойчивость частот – сходимость частоты к некоторому числу при бесконечном увеличении серии испытаний (числа n). Отметим, что это не совсем та сходимость, которая изучается в детерминированной математике, но об этом позже.

Устойчивость частот является основным объективным свойством случайных событий, на котором основана вся теория вероятностей. Это свойство подтверждается всем опытом экспериментальной науки и строго доказывается при определенных условиях (закон больших чисел).