Балансовое уравнение тепло- и массопереноса в развернутом виде можно написать, используя зависимости для внешнего и внутреннего теплообмена и массопередачи в твердой фазе (основного закона массопроводности).
Поток теплоты от теплоносителя к материалу по уравнению Ньютона-Рихмана (для конвективного теплообмена):
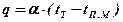 ,
,
где a – коэффициент теплоотдачи от теплоносителя к поверхности материала; tт, tп.м – соответственно, средняя температура теплоносителя и поверхности материала.
Расход теплоты на испарение влаги:
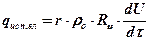 ,
,
где r – теплота испарения; ρо – плотность сухого материала; 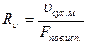 – отношение объема сухого материла к его поверхности, с которой происходит испарение (характеристический размер тела); dU / dt – скорость испарения.
– отношение объема сухого материла к его поверхности, с которой происходит испарение (характеристический размер тела); dU / dt – скорость испарения.
Расход теплоты на нагрев материала теплопроводностью по уравнению Фурье:
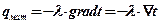
Поток теплоты за счет потока движущейся внутри материала массы влаги:
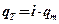 , (а)
, (а)
где i – теплосодержание (энтальпия) перемещающейся влаги; qm – суммарный поток влаги за счет градиента влагосодержания, температуры и давления.
Определим сначала qm. Для этого введем понятие потенциала переноса массы θ по аналогии с тепловым потенциалом (температурой) и удельной влагоемкости (по аналогии с удельной теплоемкостью) сm.
Обозначим коэффициент массопроводности через λm, тогда плотность потока массы:
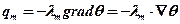 (11.26)
(11.26)
Удельная влагоемкость:
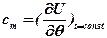 ,
,
где (∂U / ∂θ)t = const – частная производная от удельного влагосодержания по потенциалу массопереноса при постоянной температуре.
Потенциал переноса массы зависит в основном от градиента влагосодержания, температуры и давления.
Если t = const и и p=const, то θ = f(U) – будет однозначной функцией влагосодержания. В этом случае:
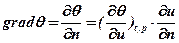 или
или 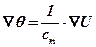 (11.27)
(11.27)
Подставив значение 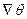 в (11.26), получим величину единичного – частного при постоянных t и p – потока массы qmu за счет градиента U (
в (11.26), получим величину единичного – частного при постоянных t и p – потока массы qmu за счет градиента U (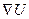 ):
):
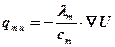 (11.28)
(11.28)
Умножив и разделив правую часть (11.28) на ρо, получим:
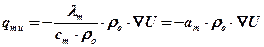 , (11.29)
, (11.29)
где ρо – плотность абсолютно сухого вещества.
Здесь коэффициент 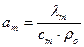 по своему физическому смыслу является аналогом коэффициента температуропроводности
по своему физическому смыслу является аналогом коэффициента температуропроводности 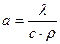 . Поэтому
. Поэтому 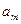 назвали коэффициентом потенциалопроводности.
назвали коэффициентом потенциалопроводности.
По физическому смыслу ат – величина, характеризующая скорость выравнивания влагосодержания в теле материала.
А.В. Лыков впервые установил, что наличие градиента температуры вызывает в материале перемещение влаги в направлении теплового потока. Это явление было названо термовлагопроводностью.
Если U = const и p = const, то θ = f(t), а закон переноса можно записать так:
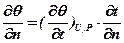 или
или 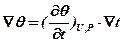 . (11.30)
. (11.30)
Подставив значение 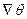 из (11.30) в (11.26), получим величину частного потока массы в материале за счет термовлагопроводности
из (11.30) в (11.26), получим величину частного потока массы в материале за счет термовлагопроводности
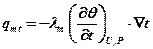 .
.
Умножив и разделив правую часть на ст ∙ ρ0 и обозначив ст ∙ (∂θ / ∂t)U,P = δ, получим:
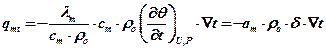 ,
,
где δ – термоградиентный коэффициент, учитывающий влияние на коэффициент потенциалопроводности ат отношения перепада влагосодержаний к перепаду температур.
Если U = const и t = const, то θ будет однозначной функцией давления и закон переноса массы для частного потока qmp (перенос за счет градиента давления) можно записать:
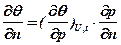 или
или 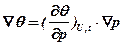 .
.
Подставив значение 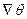 в (11.26), получим для частного потока массы:
в (11.26), получим для частного потока массы:
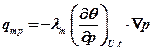 .
.
Умножив и разделив правую часть на ст ∙ ρ0 и обозначив ст ∙ (∂θ / ∂p)U,t = δР, будем иметь:
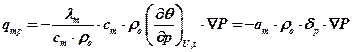 ,
,
где δР – коэффициент, учитывающий влияние на ат отношения изменения массопереноса к перепаду давления.
Обозначив
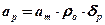 ,
,
получим
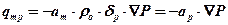 ,
,
где ар – коэффициент массопроницаемости.
Таким образом, общий (суммарный) поток влаги:
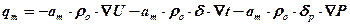
Подставив qm в уравнение (а), получим уравнение, определяющее распространение теплоты в теле при наличии массообмена:
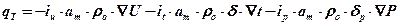 ,
,
где iu, it, ip – количество теплоты, перемещающееся соответственно с потоками массы за счет градиентов влагосодержания (U), температуры (t) и давления (p).
Балансовое уравнение тепло- и массопереноса при сушке в развернутом виде:
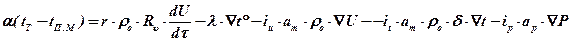
 2014-02-13
2014-02-13 2547
2547
