Пример 1. Найти пределы функции не пользуясь правилом Лопиталя:
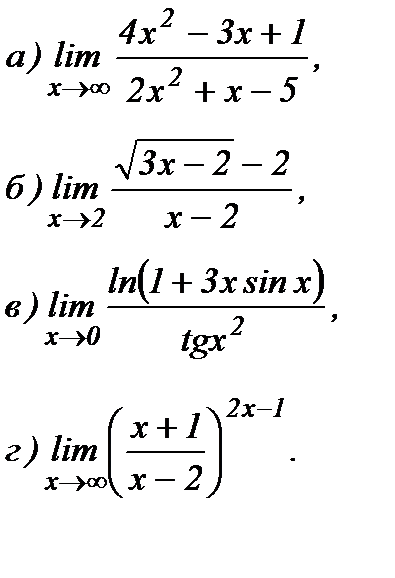
Решение.
а) Под знаком предела имеется дробная рациональная функция и при х→∞ получается неопределенность вида 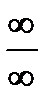 . Чтобы найти предел дробной рациональной функции
. Чтобы найти предел дробной рациональной функции  при х→∞, необходимо предварительно числитель и знаменатель дроби разделить на хn, где n – наивысшая степень многочленов Р(х) и Q(x). Разделим числитель и знаменатель данной дроби на х2 и применим основные теоремы о пределах и свойствах бесконечно малых величин:
при х→∞, необходимо предварительно числитель и знаменатель дроби разделить на хn, где n – наивысшая степень многочленов Р(х) и Q(x). Разделим числитель и знаменатель данной дроби на х2 и применим основные теоремы о пределах и свойствах бесконечно малых величин:
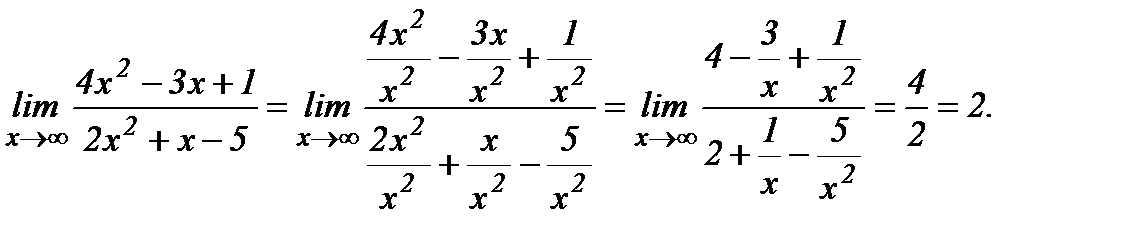
б) Непосредственная подстановка предельного значения аргумента х=2 приводит к неопределенности вида 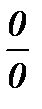 . Чтобы раскрыть эту неопределенность, умножим числитель и знаменатель дроби на сумму
. Чтобы раскрыть эту неопределенность, умножим числитель и знаменатель дроби на сумму 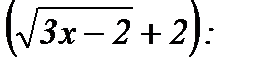
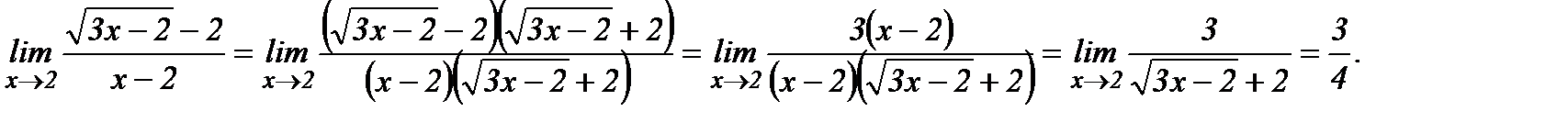
в) Непосредственная подстановка предельного значения аргумента х=0 приводит к неопределенности 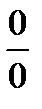 . Известно, что при нахождении предела отношения двух бесконечно малых величин можно каждую из них (или только одну) заменить другой бесконечно малой, ей эквивалентной.
. Известно, что при нахождении предела отношения двух бесконечно малых величин можно каждую из них (или только одну) заменить другой бесконечно малой, ей эквивалентной.
Так как при х→∞ ln(1 + x)~ x, tg x ~ x, то ln(1 + 3x sin x) ~3x sin x, tg x2~ x2 и 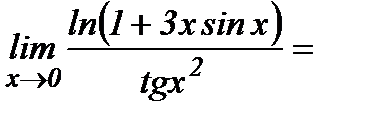
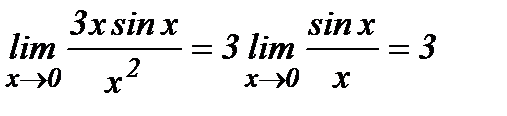
(используя 1-ый замечательный предел 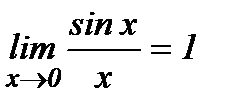 ).
).
г) При х→∞ основание 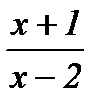 стремится к 1, а показатель степени (2х – 1)→∞. Следовательно, имеем неопределенность вида 1∞. Для ее раскрытия будем использовать II замечательный предел
стремится к 1, а показатель степени (2х – 1)→∞. Следовательно, имеем неопределенность вида 1∞. Для ее раскрытия будем использовать II замечательный предел 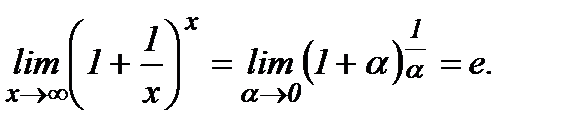
Представим основание в виде суммы: единицы и некоторой бесконечно малой величины:
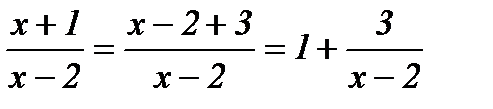 .
.
Тогда
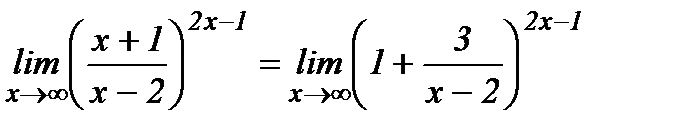 .
.
Положим х – 2 = 3у; при х → ∞ переменная у → ∞. Выразим показатель степени через новую переменную у. Так как х = 3у + 2, то 2х -1 = 2(3у + 2) – 1 = 6у + 3. Таким образом,
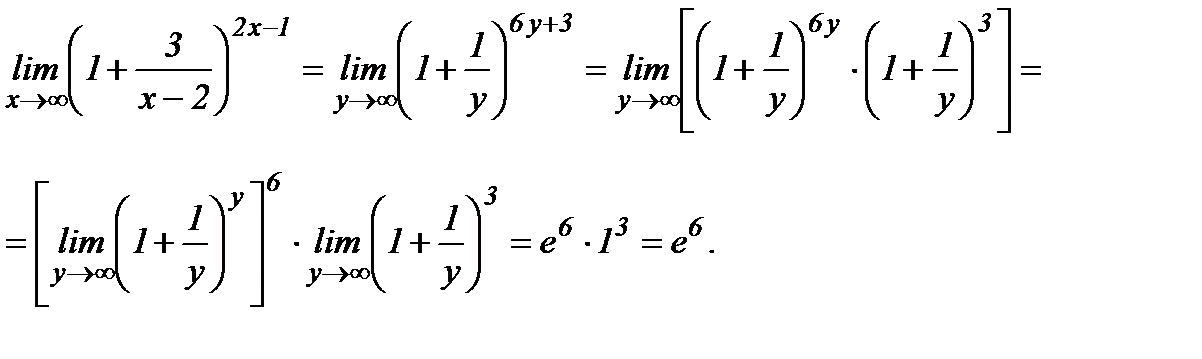
Производная и ее приложения
Основные правила и формулы дифференцирования:
1. y = c, где c=const, 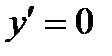 .
.
2. y = x, y'=1.
3. 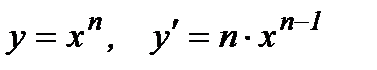 .
.
4. 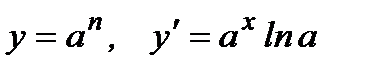 .
.
5. 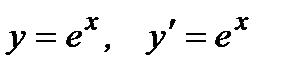 .
.
6. 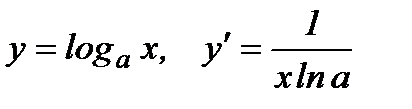 .
.
7. 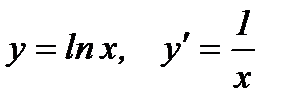 .
.
8. 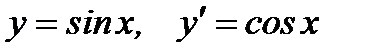 .
.
9. 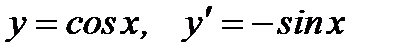 .
.
10. 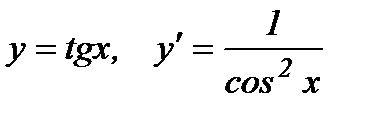 .
.
11. 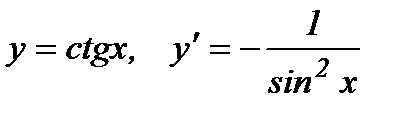 .
.
12. 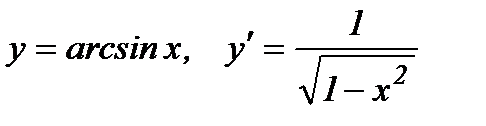 .
.
13. 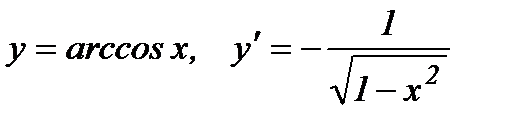 .
.
14. 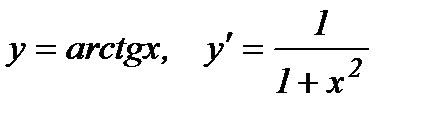 .
.
15. 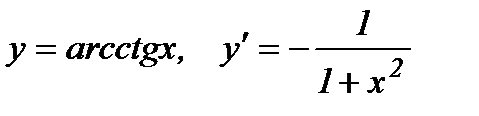 .
.
16. 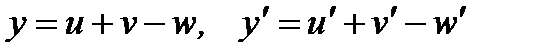 .
.
17. 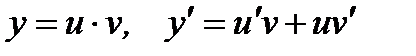 .
.
18. 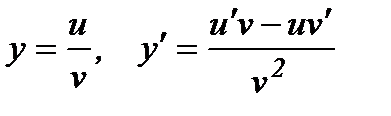 .
.
19. 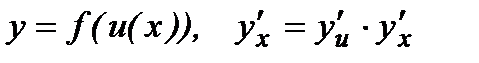 - это правило дифференцирования сложной функции.
- это правило дифференцирования сложной функции.
Пример 1. Найти производные 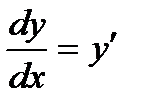 данных функций
данных функций
а) 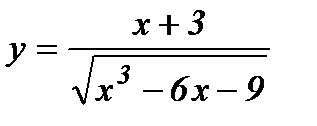 ; б)
; б) 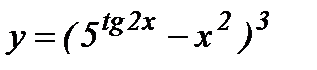 ;
;
в) 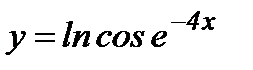 ; г)
; г) 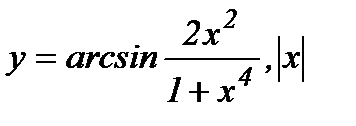 <1;
<1;
д) 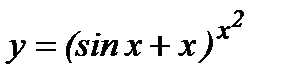 ; е)
; е) 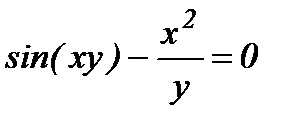 .
.
Решение:
а) Применяя правило дифференцирования дроби и формулы (3); (16), имеем
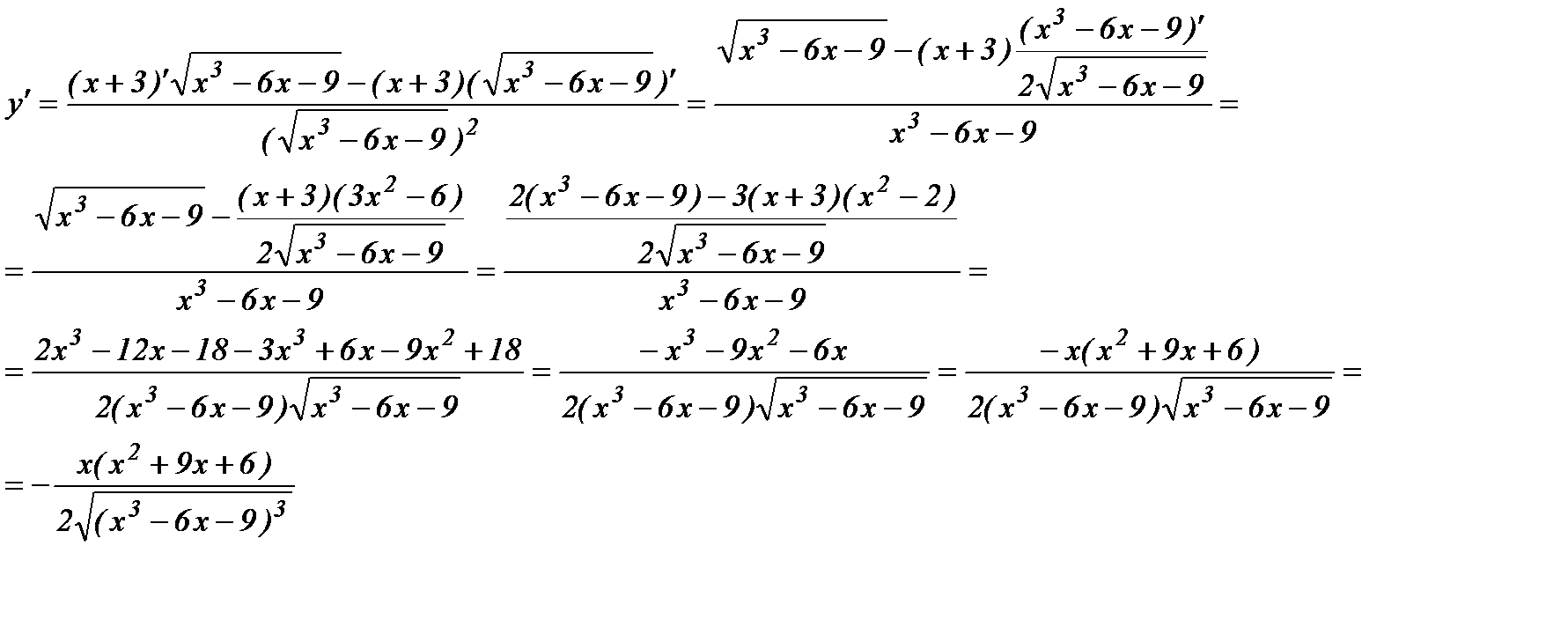
б) Последовательно применяя правило дифференцирования сложной функции, правила и формулы дифференцирования, имеем:
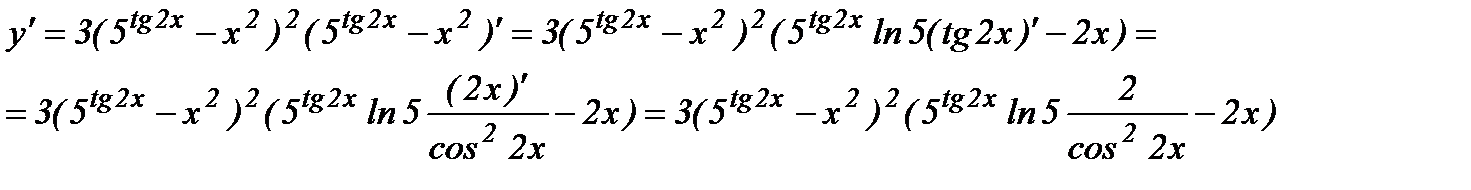
в) 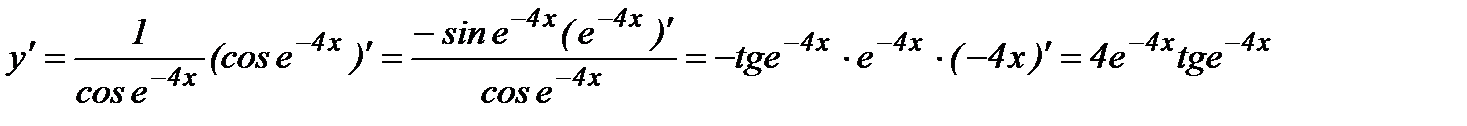
г) 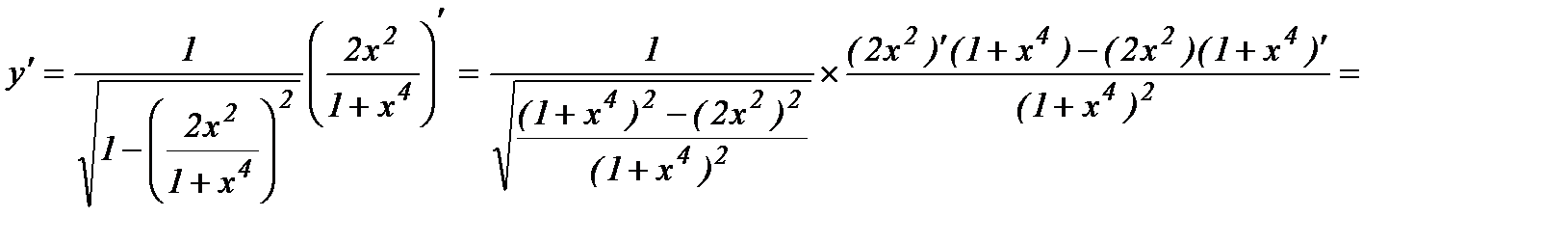
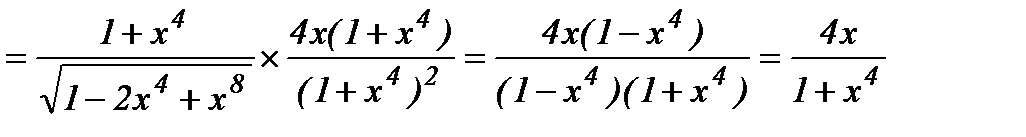
д) Предварительно прологарифмируем по основанию е обе части равенства:
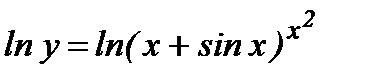 или
или 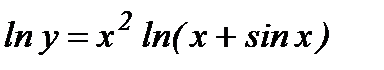 .
.
Теперь дифференцируем обе части, считая lny сложной функцией от переменной x.
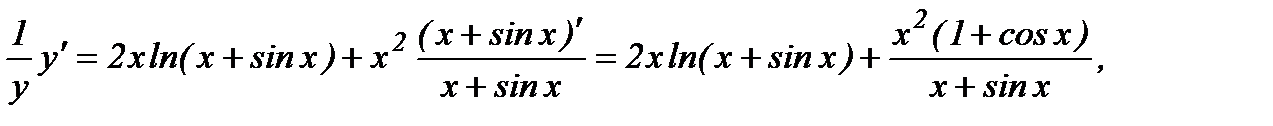 откуда
откуда
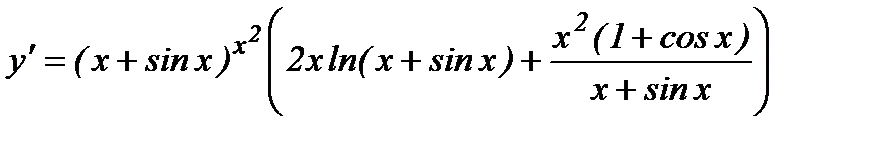 .
.
е) В данном случае зависимость между аргументом х и функцией у задана уравнением, которое не разрешено относительно функции у. Чтобы найти производную y', надо продифференцировать по х обе части заданного уравнения, считая при этом у функцией от х, а затем полученное уравнение решить относительно искомой производной y'. Имеем:
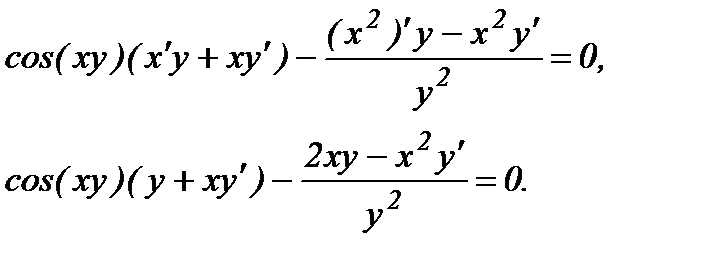
Из полученного равенства, связывающего х, у и y', находим производную y':
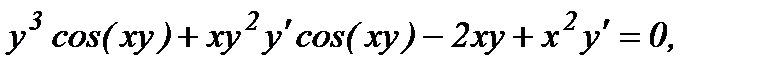
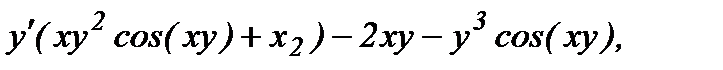 откуда
откуда 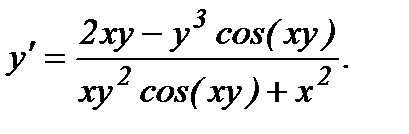
Пример 2. Найти производную второго порядка 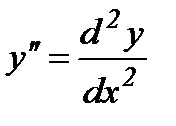 :
:
а) 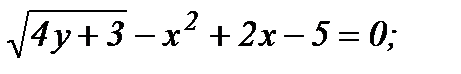
б) 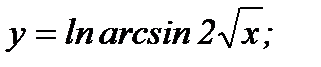
в) 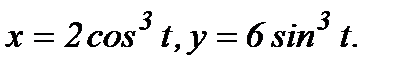
Решение:
а) Функция у задана в неявном виде. Дифференцируем по х обе части заданного уравнения, считая при этом у функцией от х:
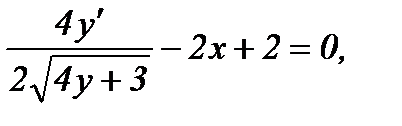 откуда
откуда 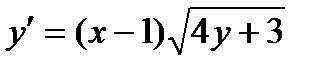 (1)
(1)
Снова дифференцируем по х обе части равенства (1):
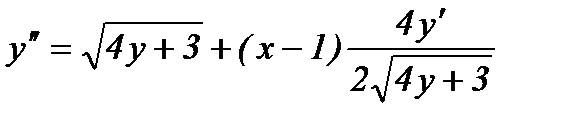 (2)
(2)
Заменив y' в (2) правой частью (1), получим
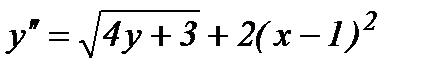 .
.
б) Найдем первую производную данной функции
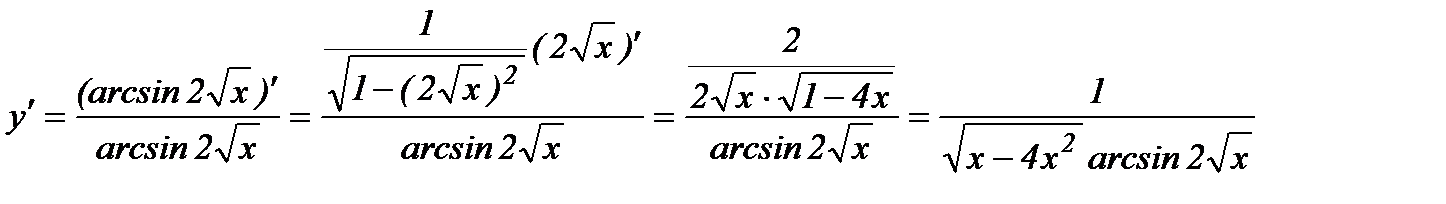 .
.
Найдем производную от первой производной, получим вторую производную функции 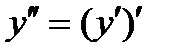 :
:
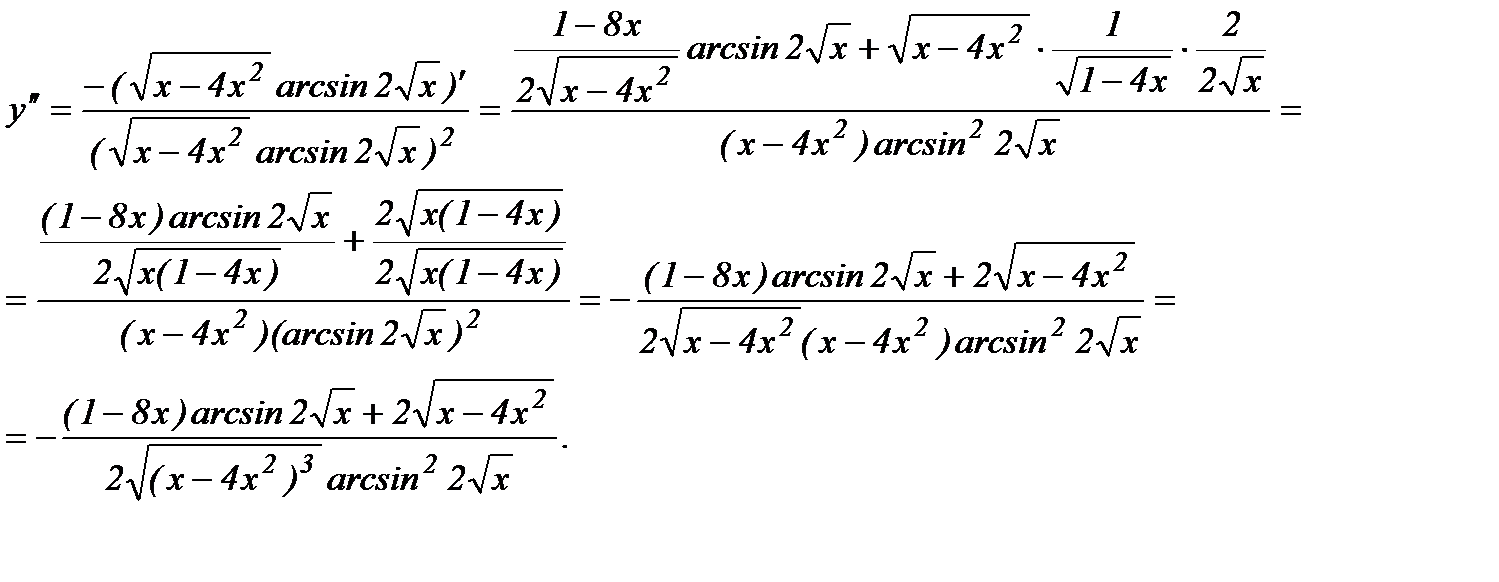
в) Зависимость между переменными х и у задана параметрическими уравнениями. Чтобы найти производную y', находим сначала дифференциалы dy и dx и затем берем отношение этих дифференциалов:
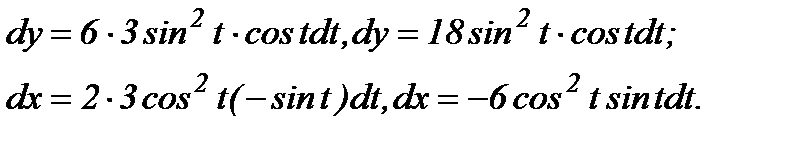
Тогда 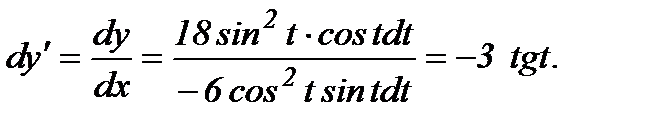
Производная второго порядка 
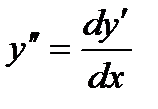 . Значит, чтобы найти y'', надо найти дифференциал dy':
. Значит, чтобы найти y'', надо найти дифференциал dy':
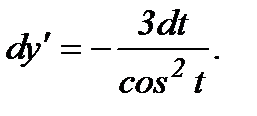
Тогда 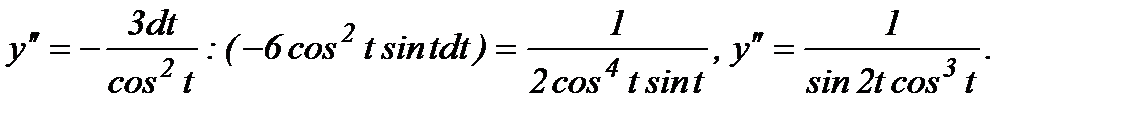
Пример 3. Исследовать методами дифференциального исчисления функцию  и, используя результаты исследования, построить ее график.
и, используя результаты исследования, построить ее график.
Решение: Исследование функции проведем по следующей схеме:
1. Найдем область определения функции.
2. Исследуем функцию на четность и нечетность.
3. Найдем точки пересечения графика функции с осями координат.
4. Исследуем функцию на непрерывность; найдем точки разрыва (если они
существуют) и установим характер разрыва.
5. Найдем асимптоты кривой у = f(x).
6. Найдем интервалы возрастания и убывания функции и ее экстремумы.
7. Найдем интервалы выпуклости и вогнутости кривой и точки ее перегиба.
Реализуем данную схему.
1. Функция определена при всех значениях аргумента х, кроме х=±2, т.е. область определения функции D(y) = (-∞;-2)U(-2;2)U(2;+∞).
2. Для установления четности или нечетности функции проверим выполнимость равенств для любых х и –х из области определения функции:
a) Если f(-x) = f(x), тогда f(x) - функция четная, т. е. ее график симметричен относительно оси О у;
b) Если f(-x) = -f(x), тогда f(x) - функция нечетная, т. е. ее график симметричен относительно начала координат т. О(0;0).
Итак, 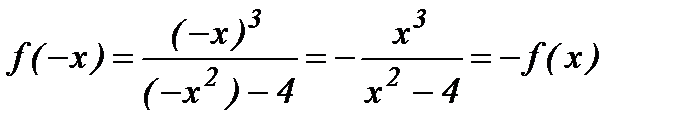 , следовательно, данная функция является нечетной.
, следовательно, данная функция является нечетной.
3. Для нахождения точек пересечения графика функции с осью Ох полагаем у=0; с осью О у — х=0.
х=0; у=0.
у=0, 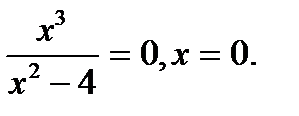
Т.е., график функции пересекает систему координат в т. О(0;0).
4. Данная функция является элементарной, поэтому она непрерывна на своей области определения D(у). Найдем односторонние пределы функции в указанных точках:
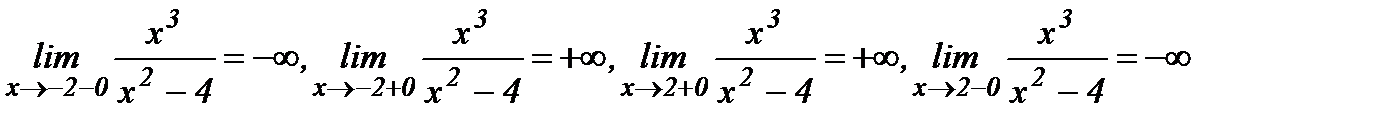 .
.
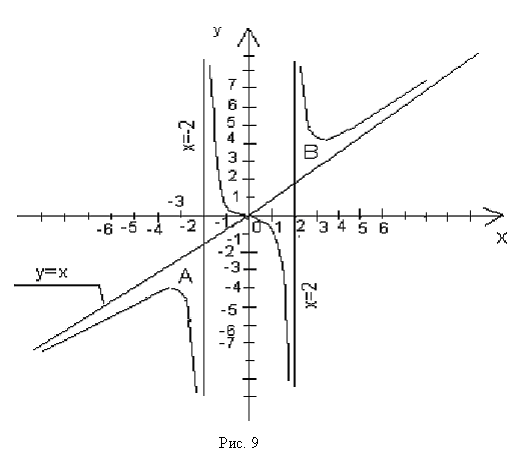
Т.о., в точках х=±2 функция имеет разрыв второго рода и прямых х = -2 и х = 2 – вертикальные асимптоты графика функции.
5. Найдем наклонные асимптоты у=kx+b, где 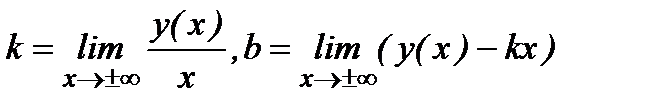
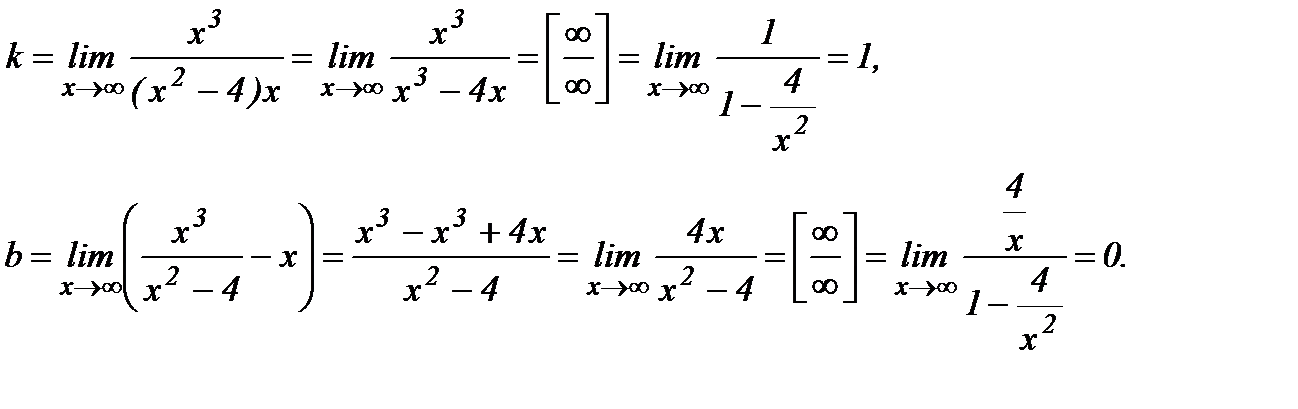
Таким образом, наклонная асимптота имеет уравнение у = х.
6. Значение f(x0) называется максимумом функции f(x), если при любом достаточно малом h>0 выполняются условия f(x0-h)<f(x0) и f(x0+h)<f(x0). Точка х0 называется в этом случае точкой максимума функции f(x) (рис.5).
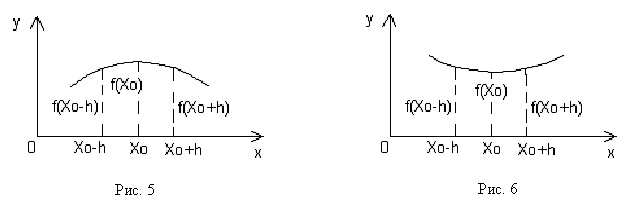
Значение f(x0) называется минимумом функции f(x), если при любом достаточно малом h>0 выполняются условия f(x0-h)>f(x0) и f(x0+h)>f(x0). Точка х0 называется в этом случае точкой минимума функции f(x) (рис. 6).
Максимум или минимум функции называется экстремумом функции.
Необходимое условие экстремума. Если функция f(x) в точке х0 имеет экстремум, то производная f'(x0) обращается в нуль или не существует.
Точка х0, в которой f'(x0)=0, называется стационарной точкой. Точки, в которых f'(x)=0 или f'(x) не существует, называются критическими точками. Не всякая критическая точка является точкой экстремума.
Функция f(x) называется возрастающей в интервале (a;b), если для любых двух точек х1и х 2 из указанного интервала, удовлетворяющих неравенству х1< х 2, выполняется неравенство f(x1)<f(х2). Если же f(x1)>f(х2) при х1< х 2, то функция f(x) называется убывающей в интервале (a;b).
Найдем производную данной функции
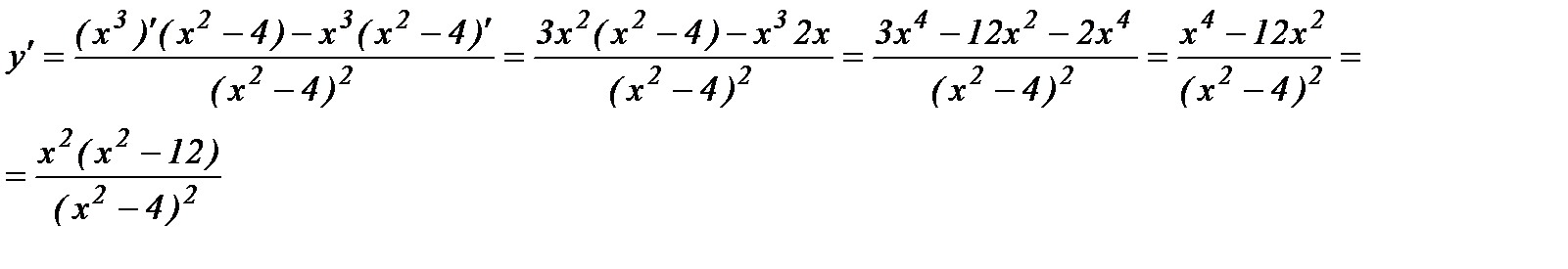
Найдем критические точки:
х1=0; х2=12, х2= 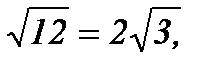
х2= 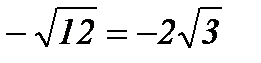 .
.
х2≠4, х≠±2 –не входят в область определения функции D(y), значит, экстремума в этих точках быть не может.
Разобьем числовую ось на 5 интервалов, составим таблицу и определим знак первой производной в каждом интервале.
| х | (-∞;-2 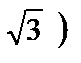 | -2 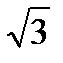 | (-2 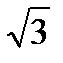 ;-2) ;-2) | (-2;2) | (2; 2 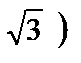 | 2 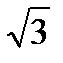 | (2 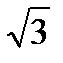 ;+∞) ;+∞) |
| у'(x) | + | - | - | - | + | ||
| у(x) | возрастает | -3 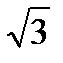 | убывает | убывает | убывает | 3 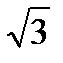 | возрастает |
| max | min |
При переходе через точку х = -2 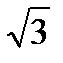 первая производная меняет свой знак с плюса на минус, поэтому в этой точке функция имеет максимум: уmax = у (-2
первая производная меняет свой знак с плюса на минус, поэтому в этой точке функция имеет максимум: уmax = у (-2 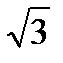 )= -3
)= -3 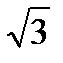 .
.
Значит, А (-2 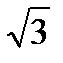 ;-3
;-3 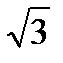 ) - точка максимума.
) - точка максимума.
При переходе через точку х = -2 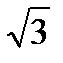 первая производная меняет свои знаки с минуса на плюс, поэтому в этой точке функция имеет минимум: уmin = у (2
первая производная меняет свои знаки с минуса на плюс, поэтому в этой точке функция имеет минимум: уmin = у (2 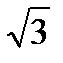 )= 3
)= 3 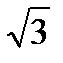 . Значит, В (2
. Значит, В (2 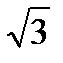 ;3
;3 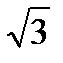 ) - точка минимума.
) - точка минимума.
7. Достаточное условие выпуклости (вогнутости) графика функции.
Если f''(x)<0 в интервале (a;b), то график функции является выпуклым в этом интервале; если же f''(x)>0, то в интервале (a;b) график функции - выпуклый.
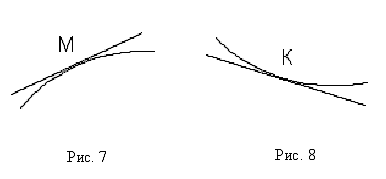
График функции у=f(х) называется выпуклым в интервале (a;b), если он расположен ниже касательной, проведенной в любой точке этого интервала (рис.7).
График функции называется вогнутым в интервале (a;b), если он расположен выше касательной, проведенной в любой точке этого интервала (рис.8).
Точка (х0;f(х0)) графика функции, отделяющая его выпуклую и вогнутую части, называется точкой перегиба.
Найдем вторую производную:
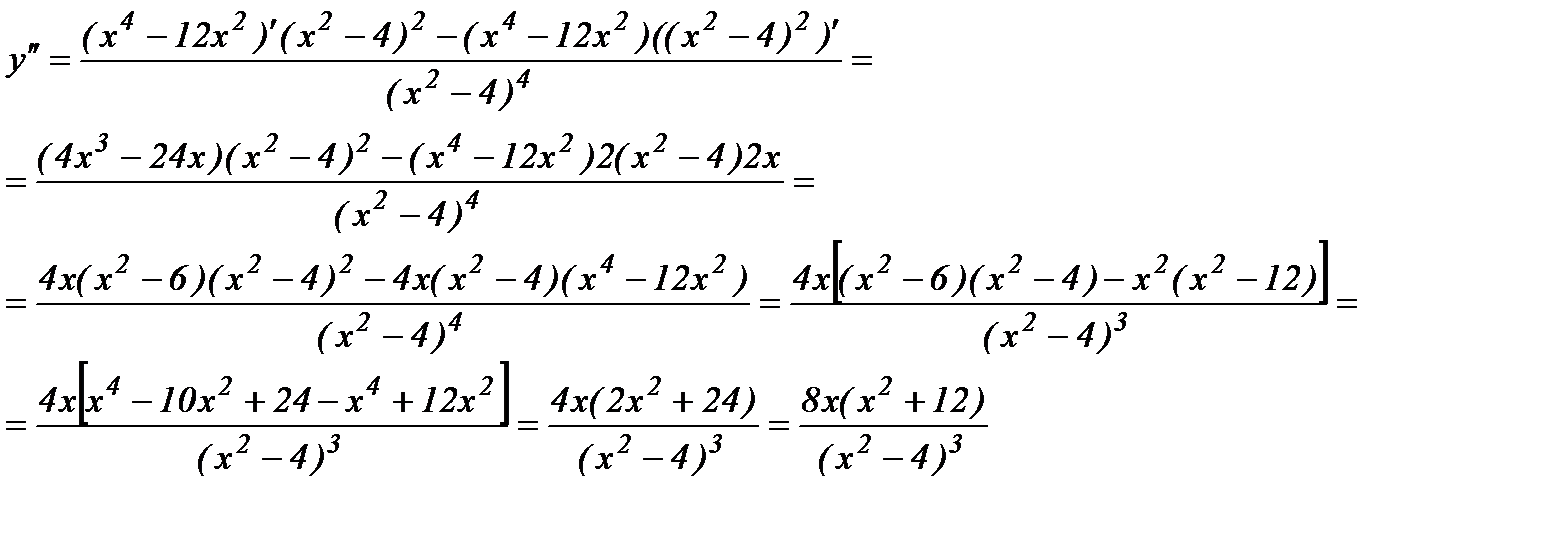
y''=0 при х=0 и y'' – не существует при х=±2; которые не входят в область определения функции.
Составим таблицу, разбив числовую ось на интервалы и определим знак второй производной в каждом из них:
| х | (-∞;-2) | (-2;0) | (0;2) | (2;+∞) | |
| y''(х) | - | + | - | + | |
| у(х) | ∩ | U | ∩ | U |
На интервалах (-∞;-2) и (0;2) y''<0 и дуга кривой выпукла; на интервалах (-2;0) и (2;+∞), y''>0 и тем самым график является вогнутым.
При переходе через точку х=0 y'' меняет свой знак, поэтому х=0 - абсцисса точки перегиба. Следовательно, С(0;0) – точка перегиба графика функции.
График исследуемой функции показан на рис.9.
Дополнительные точки для построения графика:
| х | -3 | -5 | -1 | -1,5 |
| у | -5,4 | -5,6 | 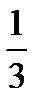 | -2 |
 2015-01-21
2015-01-21 2230
2230








