В процессе эксплуатации восстанавливаемые объекты после возникновения отказов восстанавливаются (ремонтируются или заменяются новыми) и снова включаются в работу.
Под потоком отказов (восстановлений) понимают последовательность возникающих друг за другом отказов (восстановлений работоспособного состояния) восстанавливаемого объекта.
Поток отказов простейший, если он стационарный, ординарный и без последействия.
Поток отказов стационарный, если вероятность появления определенного числа отказов на заданном интервале времени зависит только от длительности этого интервала и не зависит от места расположения его на оси времени.
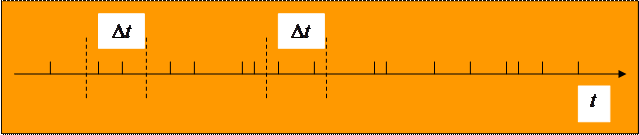
Поток отказов ординарный, если вероятность появления более одного отказана на заданном интервале времени пренебрежимо мала по сравнению с вероятностью возникновения одного отказа.
Поток отказов без последействия, если для двух не перекрывающихся интервалов времени число отказов, появляющихся на одном из них, не зависит от того, сколько отказов возникло на другом.
Аналогичными свойствами обладает простейший поток восстановлений.
Параметр потока отказов есть отношение математического ожидания числа отказов восстанавливаемого объекта к суммарной наработке его:

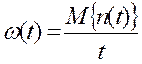 (31)
(31)
где M{n(t)} – математическое ожидание числа отказов n за суммарную наработку t. Это математическое определение.
Например (рис.), отказы объекта происходят в случайные моменты времени ti. Замена отказавших элементов происходит мгновенно. За суммарную наработку t происходит n(t) отказов.
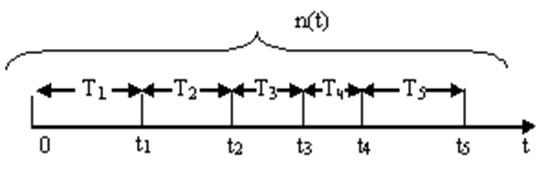
Рис.4. Поток отказов
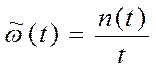 (32)
(32)
Средняя наработка на отказ. Средняя наработка на отказ есть отношение суммарной наработки восстанавливаемого объекта к математическому ожиданию числа отказов его в течение этой наработки:
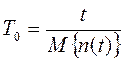 (33)
(33)
Это математическое определение.
Сравните этот результат с формулой (31).
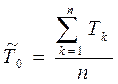 (34)
(34)
где Тк – наработка объекта между (k-1)- м восстановлением и k -м отказом.
Известно, что для экспоненциального закона надежности
ω(t)=λ и Т0=Тср,
т.е. параметр потока отказов численно равен интенсивности отказов, а средняя наработка на отказ – средней наработке до отказа.
Вероятность восстановления объекта. Если Тв – случайное время восстановления работоспособного состояния, а 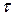 – заданное время восстановления, то вероятность восстановления объекта в течение времени
– заданное время восстановления, то вероятность восстановления объекта в течение времени 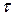
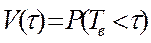 (35)
(35)
есть функция распределения времени восстановления.
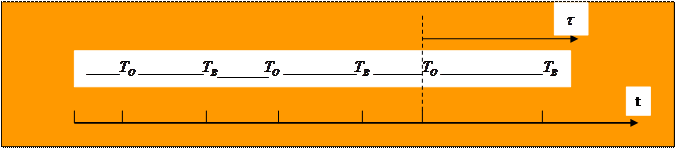
Рис. Последовательность отказов и восстановлений
Проанализируйте, как выглядит график функции 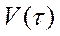 ?
?
Вероятность того, что объект не будет восстановлен в течение времени 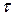 ,
,
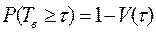 (36)
(36)
 2015-01-22
2015-01-22 979
979








