Биномиальная модель строится на весьма жестких предпосылках: известны дискретные значения будущей цены акции; известны вероятностные распределения движения цены. Модель Блэка — Шоулса является частным случаем биномиальной модели. Ее построение основывается на следующих предпосылках:
1) в качестве временного интервала между различными моментами по биномиальной модели рассматривается изменение цены акции;
2) цена акции меняется постоянно и временные интервалы в модели очень короткие (t → 0);
3) изменение цены актива является случайным процессом. Теоретически при очень коротких временных интервалах цены акции во времени а) изменяются очень слабо и изменение цены может быть описано непрерывным нормальным распределением, б) изменяются очень сильно, имеют место скачки цен, и вероятностное распределение должно характеризоваться как пуассоновское. Модель Блэка — Шоулса исходит из слабых колебаний цены и возможности использования нормального распределения;
4) нормальное распределение допускает отрицательные значения результата (кривая нормального распределения симметрична относительно центральной оси и имеет положительные и отрицательные области (см. гл. 3), что не соответствует случаю акции, цена которой не может опуститься ниже нуля (ответственность акционеров ограничена). Более того, нормальное распределение предполагает равную вероятность подъема и снижения цены, хотя в реальной жизни инфляция приводит к большему изменению цены в сторону повышения. Таким образом, принято вводить в модель распределение натурального логарифма цен акции. Кривая логнормального распределения всегда положительна и имеет правостороннюю скошенность (вероятность повышения цены);
5) отсутствуют дивидендные выплаты;
6) опцион может быть исполнен только в фиксированный момент времени (европейский опцион);
7) факторами, определяющими цену опциона, являются: а) текущая цена акции S,
б) цена исполнения К, в) срок действия опциона (время до момента исполнения опциона) t, г) безрисковая доходность, соответствующая сроку действия опциона (если срок действия опциона два года, то и kf отражает годовую процентную ставку безрискового инвестирования на два года), безрисковая доходность постоянна, д) степень изменчивости натурального логарифма цены акции (дисперсия σ 2). Дисперсия рассчитывается за прошедший период времени, как правило, сопоставимый со сроком действия опциона (если рассматривается годовой опцион, то дисперсия рассчитывается по изменениям цены акции за год, если опцион трехмесячный, то достаточно рассмотреть изменение за последние три месяца). В качестве случайной величины для расчета дисперсии берется значение l п (Pt+1/Pt);
8) нейтральность по отношению к риску;
9) отсутствуют трансакционные издержки и несовершенства рынка.
Модель определяет равновесную цену колл, которая не позволяет получать арбитражный доход. Если в какой-то момент действительная цена опциона отличается от оценки по модели, то инвестор имеет возможность сформировать портфель путем продажи колл-опционов и покупки акций и без риска получить доходность, превышающую процентную ставку. Рост таких сделок приведет к выравниванию модельной оценки и действительной цены.
Модель Блэка — Шоулса:
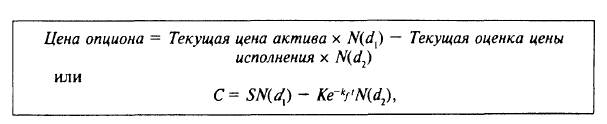
где 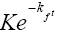 — текущая оценка (РV) цены исполнения при непрерывном дисконтировании (см. Приложение 1); kf — ставка процента (безрисковая доходность); t — срок действия опциона, т.е. число лет между сегодняшним моментом и моментом исполнения опциона; е — основание логарифма, е = 2,71828;
— текущая оценка (РV) цены исполнения при непрерывном дисконтировании (см. Приложение 1); kf — ставка процента (безрисковая доходность); t — срок действия опциона, т.е. число лет между сегодняшним моментом и моментом исполнения опциона; е — основание логарифма, е = 2,71828;
N(d) — вероятность того, что при нормальном распределении со средней, равной нулю, и стандартном отклонении, равном единице, результат будет меньше d (см. параграф 3.2 и табл. 6 Приложения 2 "Таблица накопленного нормального распределения N(X)", иногда называемую "Таблица интегральной функции плотности нормального распределения").
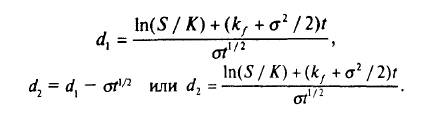
Идея модели Блэка — Шоулса также сводится к формированию портфеля путем покупки акций и привлечения денежных средств. Аналогом покупки колл-опциона рассматривается следующее формирование портфеля:

Например, рассмотрим корпорацию "Вепатор", имеющую на конец 1996 г. 3 млн. варрантов сроком на 5 лет (до 2001 г.). Цена исполнения 80 долл. Текущая цена акции 60 долл. Пятилетние государственные облигации в текущий момент обеспечивают доходность 10% годовых. Дисперсия по годовым колебаниям цен акций данной корпорации равна 0,14. Подставив исходные данные в модель, получаем:
1) d1 = [In (60/80) + (0,1 + 0,14/2) х 5] / (0,14 х 5)1/2 = 0,562 / 0,836 = 0,672, d2 = d1 - (0,14 х 5)|/2 = 0,672 - 0,836 = -0,164.
По таблице накопленного нормального распределения N(X) для Х > 0 (табл. 6 Приложения 2) находим N(d1) = N(0,672) = 0,749, N (d2) = N(-0,164) = 0,435; 2) 60 х 0,749 - (0,435 х 80)/ е 0,1 x 5 = Цена варранта = 44,94 -34,8/1,6487 = 23,84.
 2015-01-30
2015-01-30 1151
1151
