Теплопроводность при стационарном режиме

Общие положения

Учебно-методическое пособие к практическим занятиям по теплопередаче предназначено для закрепления теоретических знаний, а также для приобретения навыков теплотехнических расчетов.

Для облегчения решения задач дана подборка основных расчетных соотношений, а также приведен необходимый справочный материал.

Выполнение задач рекомендуется проводить в следующей последовательности:

1. Внимательно прочитать и выполнить в указанной форме условие задачи;

2. Составить схему для лучшей наглядности, если это необходимо;

3. Записать расчетное соотношение и по возможности вывести формулу для расчета искомой величины в общем виде;

4. Выписать из справочных таблиц дополнительно необходимые данные для расчетов и привести все физические величины к одной размерности;

5. Провести вычисления в развернутом виде и написать ответ с соответствующей размерностью.

Решение задач должно сопровождаться кратким пояснительным текстом. Все размерные физические величины должны быть записаны со своей размерностью. После решения задачи должен быть приведен краткий анализ полученных результатов, если это необходимо по условию задачи.

Теплопроводность представляет собой молекулярный перенос теплоты в телах (или между ними), обусловленный переменностью температуры в рассматриваемом пространстве.

Теплопроводность стационарна, если температурное поле не зависит от времени, т.е. dt / d t = 0. Аналитическое выражение стационарного температурного поля:

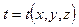(1.1)

Основной задачей аналитической теории теплопроводности является отыскание температурного поля и расчет теплового потока, переносимого через некоторую поверхность F.

Температурное поле рассчитывается на основании уравнения теплопроводности:

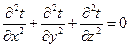, (1.2)

с соответствующими граничными условиями, а тепловой поток вычисляем с помощью закона Фурье:

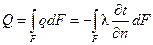, (1.3)

где n – нормаль к поверхности.

Для многослойных стенок правильной геометрической формы получена следующая формула для расчета тепловых потоков и температур граничных поверхностей:

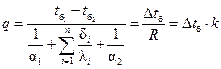, (1.4)

где t _б1 и t _б2 – температуры на боковых поверхностях стенки;

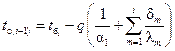, (1.5)

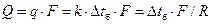, (1.6)

– для цилиндрической стенки.

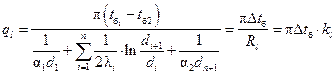, (1.7)

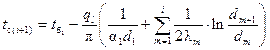
(1.8)

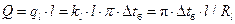, (1.9)

– для тонкостенной цилиндрической стенки (d ₂/ d ₁)<1,8 вычисление коэффициента теплопередачи можно производить по формуле для плоской стенки, при этом полный тепловой поток рассчитывается следующим образом:

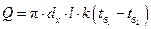, (1.10)

где в качестве d_x берем со стороны меньшего из коэффициентов теплоотдачи a.

При наложении тепловой изоляции на цилиндрическую стенку материал изоляции необходимо выбирать из условия:

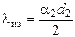. (1.11)

1-1. Вычислить плотность теплового потока через плоскую однородную стенку, толщина которой значительно меньше ширины и высоты, если стенка выполнена:

а) из стали [l = 40 Bт/(м×К)],

б) из бетона [l = 1,1 Bт/(м×К};

в) из диатомитового кирпича [l = 0,11 Вт/(м×К)].

Во всех трех случаях толщина стенки d = 50 мм Температуры на поверхностях стенки поддерживаются постоянными t _c1 = 100° C и t _c2 = 90° С.

Ответ. Для стальной стенки q = 8000 Вт/м², для бетонной стенки q = 220 Вт/м², для стенки из диатомитового кирпича q = 22 Вт/м².

1-2. Плотность теплового потока через плоскую стенку толщиной d = 50 мм q = 70 Вт/м². Определить разность температур на поверхностях стенки и численные значения градиента температуры в стенке, если она выполнена:

а) из латуни [l = 70 Bт/ (м ×К)];

б) из красного кирпича [l = 0,7 Bт/(м ×К)];

в) из пробки [l = 0,07 Вт/(м× К)].

Ответ. Для латунной стенки D t = 0,05 °С и ½ grad t ½ = l °С/м;

для кирпичной стенки D t = 5 °С ½ grad t ½ = 100°С/м;

для пробковой стенки D t = 50 °C D½ grad t ½ = 1000°C/м;

1-3. Определить потерю теплоты Q, Вт, через стенку из красного кирпича длиной l = 5 м, высотой h = 4 м и толщиной d = 0,250 м, если температуры на поверхностях стенки поддерживаются t _c1 = 110 °С и t _c2 = 40 °С Коэффициент теплопроводности красного кирпича l = 0,70 Вт/(м ×К).

Ответ. Потери теплоты Q = 3920 Вт.

1-4. Определить коэффициент теплопроводности материала стенки, если при толщине ее d = 40 мм и разности температур на поверхностях D t = 20 °C плотность теплового потока q = 145 Вт/м².

Ответ. Коэффициент теплопроводности l = 0,29 Вт/(м ×К).

1-5. Плоскую поверхность необходимо изолировать так, чтобы потери теплоты с единицы поверхности в единицу времени не превышали 450 Вт/м² Температура поверхности под изоляцией t _c1 = 450 °C, температура внешней поверхности изоляции t _c2 = 50° C Определить толщину изоляции для двух случаев:

a) изоляция выполнена из совелита, для которого

l = 0,09 + 0,0000874× t;

б) изоляция выполнена из асботермита, для которого

l = 0,109 + 0,000146× t.

Ответ. а) d = 100 мм; б) d =130 мм.

1-6. Плоская стенка выполнена из шамотного кирпича толщиной d = 250 мм. Температура ее поверхностей: t _с1 = 1350 °С и t _с2 = 50 °С. Коэффициент теплопроводности шамотного кирпича является функцией от температуры l = 0,838 (1+0,0007× t). Вычислить и изобразить в масштабе распределение температуры в стенке.

Ответ.

х, мм
t, °С

Распределение температуры в стенке показано на рис. 1-1.

Решение. В случае линейной зависимости коэффициента теплопроводности oт температуры плотность теплового потока, Вт/м²,

q = l_ср(t _c1 - t _c2)/d,

где средний коэффициент теплопроводности, Bт/(м ×К),

l_cр = l₀(1 + b_l(t _c1 + t _c2)/2).

В рассматриваемом случае

l_ср = 0,838(1 + 0,0007×(1350 + 50)/2) = 1,25 Вт/ (м×К)

и

q = 1,25/0,25 (1350 - 50) = 6500 Вт/м².

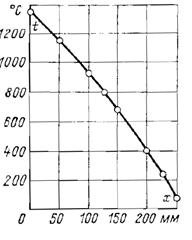
Рис. 1-1. К задаче 1-6.

Температура на любом расстоянии х от поверхности стенки определяется по формуле

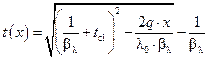
Подставив известное значение q и найденное значение q, получим:

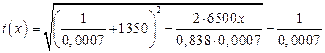
откуда

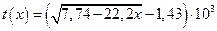, °C

Подставив в полученное уравнение значения х, выраженные в метрах, найдем соответствующие значения температуры стенки.

1-7. Температуры на поверхностях шамотной стенки, толщина которой d = 200 мм, равны: t _с1 = 1000 °C и t _c2 = 200 °С. Коэффициент теплопроводности шамота изменяется в зависимости от температуры по уравнению

l = 0,813 + 0,000582× t.

Показать, что плотность теплового потока q, Вт/м², в случае линейной зависимости коэффициента теплопроводности от темпера туры может быть вычислена по формуле для постоянного коэффициента теплопроводности, взятого при средней температуре стенки. Найти ошибку в определении температуры в точках х = 57,5, 110 и 157,5 мм, если вычисления производятся по значению коэффициента теплопроводности, среднему для заданного интервала температур и построить график распределения температуры в стенке.

Ответ. q = 4650 Вт/м²

x, мм	t x,°C
l = lср = const	l = 0,813+5,82×10-4
57,5 157,5

Распределение температуры в стенке показано на рис. 1-2.

1-8. Плоская стенка бака площадью F = 5 м² покрыта двухслойной тепловой изоляцией. Стенка бака стальная, толщиной d₁ = 8 мм, с коэффициентом теплопроводности l₁ = 46,5 Вт/(м×К). Первый слой изоляции выполнен из новоасбозурита толщиной d₂ = 50 мм, коэффициент теплопроводности которого определяется уравнением

l₂ = 0,144+0,00014 t.

Второй слой изоляции толщиной d₃ = 10 мм представляет собой штукатурку (известковую), коэффициент теплопроводности которой l₃ = 0,698 Вт/(м×К), Температуры внутренней поверхности стенки бака t _c1 = 250 °C и внешней поверхности изоляции t _с4 = 50 °C. Вычислить количество теплоты, передаваемой через стенку, температуры на границах слоев изоляции и построить график распределения температуры.

Ответ. Тепловой поток через стенку Q = 3170 Вт. Температуры на границах сдоев изоляции t _c2 = 249,9 °С и t _c3 = 59 °С.

1-9. Обмуровка печи состоит из слоев шамотного и красного кирпича, между которыми расположена засыпка из диатомита (рис. 1-3) Толщина шамотного слоя d₁ = 120 мм, диатомитовой засыпки d₂ = 50 мм и красного кирпича d₃ = 250 мм. Коэффициенты теплопроводности материалов соответственно равны:

l₁ = 0,93; l₂ = 0,13 и l₃ = 0,7 Вт/ (м × К).

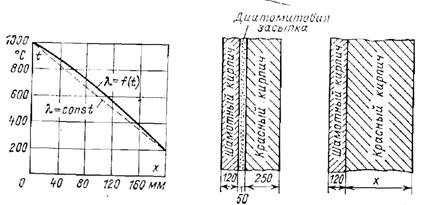
Рис. 1-2. К задаче 1-7 Рис. 1-3. К задаче 1-9.

Какой толщины следует сделать слой из красного кирпича d₃, если отказаться от применения засыпки из диатомита, чтобы тепловой поток через обмуровку остался неизменным?

Ответ. Толщина слоя красного кирпича должна быть равна 500 мм.

1-10. Стенка неэкранированной топочной камеры парового котла выполнена из слоя пеношамота толщиной d₁ = 125 мм и слоя красного кирпича толщиной d₂ = 500 мм. Слои плотно прилегают друг к другу. Температура на внутренней поверхности камеры t _с1 = 1100 °С, а на наружной t _с3 = 50 °С (рис. 1-4). Коэффициент теплопроводности пеношамота l₁ = 0,28+0,00023 t, красного кирпича l₂ = 0,7 Вт/(м×К).

Вычислить тепловые потери через 1 м² стенки топочной камеры и температуру в плоскости соприкосновения слоев.

Ответ. Тепловые потери q = 1090 Вт/м². Температура в плоскости соприкосновения слоев t _с2 = 828 °С.

1-11. Толщину слоя красного кирпича в стенке топочной камеры, рассмотренной в задаче 1-10, решено уменьшить в 2 раза, а между слоями поместить слой засыпки из диатомитовой крошки (рис 1-5), коэффициент теплопроводности которой l = 0,113+0,00023 t. Какую нужно сделать толщину диатомитовой засыпки, чтобы при тех же температурах на внешних поверхностях стенки, что и в задаче 1-10, потери теплоты оставались неизменными?

Ответ. Толщина диатомитовой засыпки должна быть d = 94 мм.

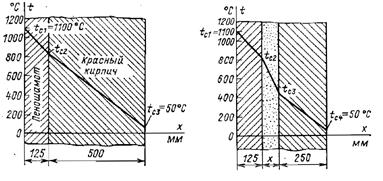
Рис. 1-4. К задаче 1-10. Рис. 1-5. К задаче 1-11.

Решение. Так как тепловые потери q = 1090 Вт/м² должны оставаться неизменными, то температуру в плоскости соприкосновения диатомитовой засыпки и красного кирпича найдем по уравнению

t _c3 = t _c1+ q × d₂/l₂ = 50 +1090 × 0,25/0,7 = 439 °C.

Среднее значение коэффициента теплопроводности диатомитовой засыпки найдется из уравнения

l_ср = а + b (t _c3 + t _c2) /2= 0,113 + 0,00023(828 + 439) /2 = 0,259 Вт/ (м×К).

Тогда толщина засыпки будет равна

d = (D t _зас / q)×l_ср = [(828439)/1090] ×0,259 = 0,0936 м; d» 94 мм.

1-12. Стены сушильной камеры выполнены из слоя красного кирпича толщиной d₁ = 250 мм и слоя строительного войлока. Температура на внешней поверхности кирпичного слоя t _c1 = 110° C и на внешней поверхности войлочного слоя t _с3 = 25°С

Коэффициент теплопроводности красного кирпича l₁ = 0,7 Вт/ (м×К) и строительного войлока l₂ = 0,04б5 Вт/(м×К). Вычислить температуру в плоскости соприкосновения слоев и толщину войлочного слоя при условии, что тепловые потери через 1 м² стенки камеры не превышают q = 110 Вт/м².

Ответ. Температура в плоскости соприкосновения слоев t _c2 = 70,7 °С. Толщина войлочного слоя d₂ » 19 мм.

1-13. В приборе для определения коэффициента теплопроводности материалов между горячей и холодной поверхностями расположен образец из испытуемого материала (рис. 1-6). Образец представляет собой диск диаметром d = 120 мм и толщиной d = 20 мм.

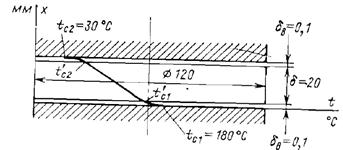
Рис. 1-6. К задаче 1-13.

Температура горячей поверхности t _с1 = 180°C, холодной t _с2 = 30° С. Тепловой поток через образец после установления стационарного процесса Q = 50,6 Вт. Благодаря защитным нагревателям радиальные потоки теплоты отсутствуют. Вследствие плохой пригонки между холодной и горячей поверхностями и образцом образовались воздушные зазоры толщиной d_в = 0,1 мм. Вычислить относительную ошибку в определении коэффициента теплопроводности D_l, если при обработке результатов измерений не учитывать образовавшихся зазоров. Коэффициент теплопроводности воздуха в зазорах отнести к температурам соответствующих поверхностей t _с1 и t _с2.

Ответ. Относительная ошибка в определении l составит D_l» 21 %.

1-14. Вычислить потери теплоты через единицу поверхности кирпичной обмуровки парового котла в зоне размещения водяного экономайзера и температуры на поверхностях стенки, если толщина стенки d = 250 мм, температура газов t _ж1 = 700 °C и воздуха в котельной t _ж2 = 30° C. Коэффициент теплоотдачи от газов к поверхности стенки a₁ = 23 Вт/ (м²×К) и от стенки к воздуху a₂ = 12 Вт/ (м²×К). Коэффициент теплопроводности стенки l = 0,7 Вт/ (м×К).

Ответ. Потери теплоты q = 1385 Вт/м². Температура на поверхностях стенки t _с1 = 640 °C и t _с2 = 145,5 °С.

1-15. Вычислить тепловой поток через 1 м² чистой поверхности нагрева парового котла и температуры на поверхностях стенки, если заданы следующие величины: температура дымовых газов t _ж1 = 1000 °С, кипящей воды t _ж2 = 200 °С; коэффициенты теплоотдачи от газов к стенке a₁ = 100 Вт/ (м²×К) и от стенки к кипящей воде a₂ = 5000 Вт/ (м²×К). Коэффициент теплопроводности материала стенки l = 50 Вт/ (м ×К) и толщина стенки d = 12 мм.

Ответ. q = 76500 Вт/м². Температуры на поверхностях стенки t _c1 = 235 °C и t _c2 = 215 °С (рис 1-7).

1-16. Решить задачу 1-15 при условии, что в процессе эксплуатации поверхность нагрева парового котла со стороны дымовых газов покрылись слоем сажи толщиной d_с = 1 мм [l_с = 0,08 Вт/ (м ×К)] и со стороны воды слоем накипи толщиной d_н = 2 мм² [l_н = 0,8 Вт/ (м×К)]. Вычислить плотность теплового потока через 1 м² загрязненной поверхности нагрева и температуры на поверхностях соответствующих слоев t _с1, t _c2, t _c3 и t _c4 (рис. 1-8). Сравнить результаты расчета с ответом задачи 1-15 и определить уменьшение тепловой нагрузки.

Ответ. Плотность теплового потока q = 31500 Вт/м². Температуры на поверхностях слоев t _c1 = 685 °C, t _c2 = 291 °С, t _c3 = 283 °С, t _c4 = 206 °C. Уменьшение тепловой нагрузки поверхности нагрева в результате загрязнения D q = 58,9 %.

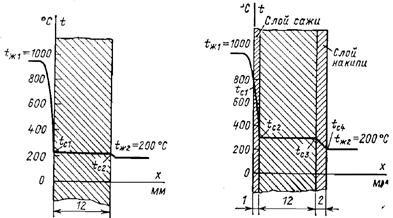
Рис. 1-7. К задаче 1-15. Рис 1-8. К задаче 1-16

1-17. Определить тепловой поток через 1 м² кирпичной стены помещения толщиной в два кирпича (d = 510 мм) с коэффициентом теплопроводности l = 0,8 Вт/(м×К). Температура воздуха внутри помещения t _ж1 = 18 °C, коэффициент теплоотдачи к внутренней поверхности стенки a₁ = 7,5 Вт/(м²×К); температура наружного воздуха t _ж2 = 30 °С; коэффициент теплоотдачи от наружной поверхности стены, обдуваемой ветром, a₂ = 20 Вт/ (м² ×К). Вычислить также температуры на поверхностях стены t _с1 и t _с2.

Ответ. Плотность теплового потока q = 58,6 Вт/м². Температуры на поверхностях стены t _с1 = 10,2 °С и t _с2 = 27,1 °С.

1-18. Решить задачу 1-17, если стена покрыта снаружи слоем тепловой изоляции толщиной 50 мм с коэффициентом теплопроводности l_из = 0,08 Вт/ (м×К). Сравнить потери теплоты через изолированную и неизолированную стенки.

Ответ. Потери теплоты через изолированную стенку q = 33,2 Вт/м². Температуры на поверхностях стены: t _c1 = 13,6 °C и t _cз = -28,3 °С Потери теплоты через неизолированную стенку на 76,5 % больше, чем через изолированную.

1-19. Вычислить плотность теплового потока q, Вт/м², в пластинчатом воздухоподогревателе и значения температур на поверхностях листов, если известно, что средняя температура газов t _ж1 = 315 °C и средняя температура воздуха t _ж2 = 135 °С, соответственно коэффициенты теплоотдачи a₁ = 23 Вт/ (м²×К) и a₂ = 30 Вт/ (м²×К). Толщина листов подогревателя d =2 мм. Коэффициент теплопроводности материала листов l = 50 Вт/ (м×К).

Ответ. q = 2200Вт/м²; t _c1 = 208,5 °С; t _c2 = 208,4 °С; t _c1 » t _c2» 208 °С.

1-20. Обмуровка печи выполнена из слоя шамотного кирпича с коэффициентом теплопроводности l = 0,84(1 + 0,695×10^-3 t) Вт/ (м×К); толщина обмуровки d = 250 мм. Определить потери теплоты с одного квадратного метра поверхности q, Вт/м², и температуры на внешних поверхностях стены, если температура газов в печи t _ж1 = 1200 °C и воздуха в помещении t _ж2 = 30 °С, коэффициент теплоотдачи от газов к стенке a₁ = 30 Вт/(м²×К) и от обмуровки к окружающему воздуху a₂ = 10 Вт/ (м²×К).

Ответ. q = 3530 Вт/м².

Решение. При заданной зависимости коэффициента теплопроводности шамотного кирпича от температуры потери теплоты можно вычислить из уравнения

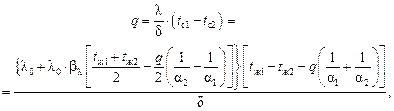
или методом последовательных приближений. Ниже приводится решение методом последовательных приближений. Задаемся средней температурой стенки t _c = 650°C. При этой температуре коэффициент теплопроводности шамотного кирпича равен l_ср = 0,84 (1 + 0,695×10^-3´´650) = 1,12 Вт/ (м×К). Определяем коэффициент теплопередачи

и плотность теплового потока

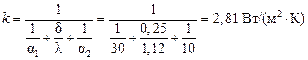
q = k (t _ж1 - t _ж2) = 2,81 (1200 - 30) = 3290 Вт/м².

При полученной плотности теплового потока вычисляем температуры па поверхностях стенки:

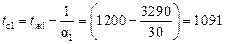°С;

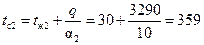°C.

Определяем среднюю температуру стенки и уточняем значение коэффициента теплопроводности: t ¢_c = 0,5 (1091 + 359) = 725° С;

l = 0,84(1+ 0,695×10^-3×^×725) = 1,265 Вт/(м×К);

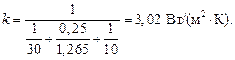
При этом плотность теплового потока

q = 3,02×(1200 - 30) = 3530 Вт/м².

При новом значении плотности теплового потока вычисляем температуры t _c1 и t _c2:

t _c1 = 1200 - 3530 ×1/30 = 1082 °С;

t _c2 = 30 + 3530 × 1/10 = 383 °C.

Определяем средние значения температуры стенки и коэффициент теплопроводности:

t _с = 0,5 ×(1082 + 383) = 732 °С;

l_ср = 0,84(1 + 0,695×10^-3×732) = 1,267 Вт/(м×К).

Так как полученное среднее значение коэффициента теплопроводности практически совпадает с принятым ранее значением, то дальнейших пересчетов делать не нужно и можно принять q = 3530 Вт/м².

1-21. В камере сгорания парового котла с жидким золоудалением температура газов должна поддерживаться равной t _ж1 = 1300 °С, температура воздуха в котельной t _ж2 = 30 °С. Стены топочной камеры выполнены из слоя огнеупора толщиной d₁ = 250 мм с коэффициентом теплопроводности

l₁ = 0,28×(l + 0,833×10^-3 t) Вт/(м×К)

и слоя диатомитового кирпича с коэффициентом теплопроводности l₂ = 0,113 (1+0,206×10^-3 t) Вт/ (м×К). Коэффициент теплоотдачи от газов к обмуровке a₁ = 30 Вт/ (м²×К) и от внешней поверхности топочной камеры к окружающему воздуху a₂ = 10 Вт/ (м²×К). Какой должна быть толщина диатомитового слоя, чтобы потери в окружающую среду не превышали 750 Вт/м²?

Ответ. Толщина диатомитового слоя должна быть d₂ = 132 мм.

1-22. Змеевики пароперегревателя выполнены из труб жароупорной стали диаметром d ₁/ d ₂ = 32/42 мм с коэффициентом теплопроводности l = 14 Вт/ (м×К). Температура внешней поверхности трубы t _c2 = 580°С и внутренней поверхности t _c1 = 450°C. Вычислить удельный тепловой поток через стенку на единицу длины трубы q_l, Вт/м.

Ответ. q_l = 42 100 Вт/м.

1-23. Паропровод диаметром 150/160 мм покрыт слоем тепловой изоляции толщиной d_из = 100 мм; коэффициенты теплопроводности стенки трубы l₁=50 Вт/ (м×К) и изоляции l_из = 0,08 Вт/ (м×К). Температура на внутренней поверхности паропровода t _с1 = 400 °C и на наружной поверхности изоляции t _с3 = 50 °С. Найти тепловые потери с 1 м паропровода и температуру на границе соприкосновения паропровода и изоляции.

Ответ. Потери теплоты с 1 м паропровода q_l = 216 Вт/м. Температура на границе соприкосновения паропровода и изоляции t _c2» 400 °С

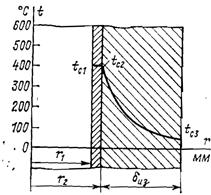
Рис. 1-9. К задаче 1-23.

1-24. Стальной трубопровод диаметром d ₁/ d ₂ = 100/110 мм с коэффициентом теплопроводности l₁=50 Вт/ (м×К) покрыт изоляцией в два слоя одинаковой толщины d₂ = d₃ = 50 мм. Температура внутренней поверхности трубы t _c1 = 250 °C и наружной поверхности изоляции t _c4 = 50 °C (рис. 1-10). Определить потери теплоты через изоляцию с 1 м трубопровода и температуру на границе соприкосновения слоев изоляции, если первый слой изоляции, накладываемый на поверхность трубы, выполнен из материала с коэффициентом теплопроводности l₂ = 0,06 Вт/ (м×К), а второй слой из материала с коэффициентом.теплопроводности l₃=0,12 Вт/ (м×К).

Ответ. Тепловые потери с 1 м трубопровода q_l = 89,5 Вт/м. Температура на границе соприкосновения слоев изоляции t _c3 = 97 °C.

1-25. Как изменятся тепловые потери с 1 м трубопровода, рассмотренного в задаче 1-24, если слои изоляции поменять местами, т. е. слой с большим коэффициентом теплопроводности наложить не- посредственно на поверхность трубы? Все другие условия оставить без изменений.

Ответ. Потери теплоты увеличатся и составят q_l = 105,5 Вт/м, Температура на границе соприкосновения слоев изоляции t _с3 = 159 °С (см. рис. 1-10).

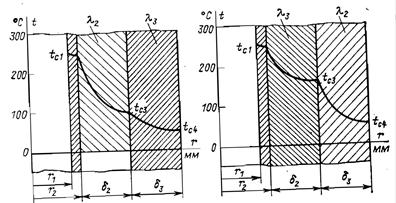
Рис. 1-10. К задачам 1-24 и 1-25.

1-26. Паропровод диаметром d ₁/ d ₂ = 160/170 мм покрыт слоем изоляции толщиной d = 100 мм с коэффициентом теплопроводности, зависящим от температуры следующим образом:

l_из = 0,062(1+0,363×10^-2 t).

Определить потери теплоты с 1 м паропровода и температуру на внутренней поверхности трубопровода, если температура наружной поверхности трубы t _c2 = 300 °С, а температура внешней поверхности изоляции не должна превышать 50 °С.

Ответ. Потери теплоты с 1 м паропровода q_l = 205 Вт/м. Температура внутренней поверхности трубопровода t _c1 = 300 °C.

1-27. Железобетонная дымовая труба (рис. 1-11) внутренним диаметром d ₂ = 800 мм и наружным диаметром d ₃ = 1300 мм должна быть футерована внутри огнеупором. Определить толщину футеровки и температуру наружной поверхности трубы t _c3 из условий, чтобы тепловые потери с 1 м трубы не превышали 2000 Вт/м, а температура внутренней поверхности железобетонной стенки t _c2 не превышала 200 °С.

Температура внутренней поверхности футеровки t _c1 = 425°C; коэффициент теплопроводности футеровки l₁ = 0,5 Вт/(м×К); коэффициент теплопроводности бетона l₂ = 1,1 Вт/ (м×К).

Ответ. d = 120 мм. Температура наружной поверхности трубы t _c3 = 59 °С.

1-28. В условиях задачи 1-27 определить толщину футеровки d если она выполнена из шамотного кирпича. Расчет произвести с учетом зависимости коэффициента l от температуры по формуле

l = 0,84+0,0006× t.

Ответ. Толщина футеровки должна быть d = 206 мм.

1-29. В приборе для определения коэффициента теплопроводности жидкостей по методу «нагретой нити» (рис. 1-12) в кольцевой зазор между платиновой нитью и кварцевой трубкой залито испытуемое трансформаторное масло. Диаметр и длина платиновой нити d ₁ = 0,12 мм и l = 90 мм; внутренний и наружный диаметры кварцевой трубки d ₂ = 1 мм и d ₃ = 3 мм; коэффициент теплопроводности кварца l = 1,4 Вт/(м×К). Вычислить коэффициент теплопроводности l_ж и среднюю температуру t _ж трансформаторного масла, если при расходе теплоты через кольцевой слой масла Q = l,8 Вт, температура платиновой нити t _c1 = 106,9 °С и температура внешней поверхности кварцевой трубки t _c3 = 30,6 °С.

Ответ. Коэффициент теплопроводности трансформаторного масла l_ж = 0,0915 Вт/ (м×К) при t _ж = 70 °С.

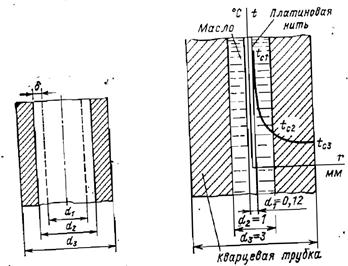
Рис. 1-11. К задаче 1-27. Рис. 1-12. К задаче 1-29.

1-30. Вычислить допустимую силу тока для медного провода d = 2 мм, покрытого резиновой изоляцией толщиной d = 1 мм, при условии, что максимальная температура изоляции должна быть не выше 60 °С, а на внешней поверхности изоляции 40 °С. Коэффициент теплопроводности резины l=0,15 Вт/ (м×К). Электрическое сопротивление медного провода R = 0,005 Ом/м.

Ответ. Допустимая сила тока I =79,8 А.

1-31. Определить площадь поверхности нагрева конвективного пароперегревателя, выполненного из труб жаростойкой стали диаметром d ₁/ d ₂ = 32/40 мм. Коэффициент теплопроводности стали l = 39,5 Вт/ (м×К). Производительность пароперегревателя Q = 61,1 кг/с пара. В пароперегреватель поступает сухой насыщенный пар при давлении р = 9,8 МПа. Температура перегретого пара на выходе t _п = 500°С. Коэффициент теплоотдачи от газов к стенке a₂ = 81,5 Вт/ (м²×К), а от стенки к пару a₁ = 1163 Вт/ (м²×К); средняя температура газов t _ж = 900 °С. Гидравлическим сопротивлением пароперегревателя пренебречь.

Ответ. Площадь поверхности нагрева пароперегревателя, рассчитанная по наружному диаметру труб, F = 1090 м².

1-32. Решить задачу (1-31), пренебрегая кривизной стенки (как для плоской стенки). Полученную площадь поверхности нагрева сравнить с результатом, полученным в задаче 1-31.

Ответ. Площадь поверхности нагрева F = 1055 м².

1-33. Найти площадь поверхности нагрева секционного водо-водяного подогревателя производительностью Q = 1500 кВт при условии, что средняя температура греющей воды t _ж1 = 115 °С, а средняя температура нагреваемой воды t _ж2 = 77 °С. Поверхность нагрева выполнена из латунных трубок диаметром d ₁/ d ₂ = 14/16 мм с коэффициентом теплопроводности l_с = 120 Вт/ (м×К). На внутренней поверхности трубок имеется слой накипи d_н = 0,2 мм с коэффициен-том теплопроводности l_н = 2 Вт/(м×К). Коэффициент теплоотдачи со стороны греющей воды a₁ = 10000 Вт/ (м²×К) и со стороны нагреваемой воды a₂ = 4000 Вт/ (м²×К). Так как отношение диаметров d ₁/ d ₂ < 1,8, то расчет можно произвести по формуле для плоской стенки.

Ответ. Площадь поверхности нагрева F = 18,l м².

1-34. Вычислить потерю теплоты с 1 м неизолированного трубопровода диаметром d ₁/ d ₂ = 150/165 мм, проложенного на открытом воздухе, если внутри трубы протекает вода со средней температурой t _ж1 = 90 °С и температура окружающего воздуха t _ж2 = -15 °С. Коэффициент теплопроводности материала трубы l = 50 Вт/ (м×К). Коэффициент теплоотдачи от воды к стенке трубы a₁ = 1000 Вт/ (м²×К) и от трубы к окружающему воздуху a₂ = 12 Вт/ (м²×К). Определить также температуры на внутренней и внешней поверхностях трубы (рис. 1-13).

Ответ. q_l = 652 Вт/м; t _c1 = 89,8 °С; t _c2 = 89,6 °С.

1-35. Определить тепловые потери с 1 м трубопровода, рассмотренного в задаче 1-34, если трубопровод покрыт слоем изоляции толщиной d₁=60 мм (рис. 1-14). Коэффициент теплопроводности изоляции l₁=0,15 Вт/ (м×К). Коэффициент теплоотдачи от поверхности изоляции к окружающему воздуху a₂ = 8 Вт/ (м²×К). Все остальные условия остаются такими же, как в задаче 1-34. Вычислить также температуры на внешней поверхности трубы t _c2 и на внешней поверхности изоляции t _c3.

Ответ. q_l = 145 Вт/м; t _c2 = 89,9 °С; t _c3 = 5,3 °С.

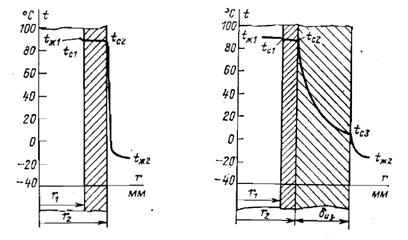
Рис. 1-13. К задаче 1-34. Рис. 1-14. К задаче 1-35.

1-36. По трубопроводу диаметром d ₁/ d ₂ = 25/29 мм [l₁ = 50 Вт/ (м×К)], покрытому изоляцией из торфолиума толщиной d₂ = 25 мм [l₂ = 0,06 Вт/ (м×К)], проходит насыщенный пар давлением 980 кПа. Определить суточную потерю теплоты (в килограммах пара) участка трубопровода длиной 30 м и температуру наружной поверхности изоляции, если коэффициент теплоотдачи от пара к стенке a₁= 2000

Вт/ (м²×К) и от внешней поверхности изоляции к окружающему воздуху a₂=10 Вт/ (м²×К). Температура окружающего воздуха t _ж2 = 10 °С.

Ответ. Суточная потеря теплоты в килограммах пара G = 105 кг/сут. Температура на внешней поверхности изоляции t _с3 = 61,2 °С.

1-37. Трубчатый воздушный подогреватель производительностью 2,78 кг/с воздуха выполнен из труб диаметром d ₁/ d ₃ = 43/49 мм. Коэффициент теплопроводности материала труб l = 50 Вт/ (м×К) Внутри труб движется горячий газ, а наружная поверхность труб омывается поперечным потоком воздуха Средняя температура дымовых газов t _ж1 = 250 °C, а средняя температура подогреваемого воздуха t _ж2 = 145 °С. Разность температур воздуха на входе и выходе из подогревателя равна d t = 250 °C. Коэффициент теплоотдачи от газов к стенке a₁ = 45 Вт/ (м²×К) и от стенки к воздуху a₂ = 25 Вт/ (м²×К). Вычислить коэффициент теплопередачи и определить площадь поверхности нагрева подогревателя Расчет произвести по формулам для 1) цилиндрической и 2) плоской стенок. Сравнить результаты вычислений.

Ответ.

1. Расчет по формуле для цилиндрической стенки дает значение коэффициента теплопередачи k_l = 0,75 Вт/ (м²×К) Площадь поверхности нагрева при этом F = 412 м²

2. Расчет по формуле для плоской стенки дает значение коэффициента теплопередачи k = l6 Вт/(м²×К). Площадь поверхности нагрева при этом F = 418 м².

1-38. Как изменятся тепловая производительность воздушного подогревателя и расход воздуха в задаче 1-37, если со стороны дымовых газов в процессе эксплуатации образуется слой сажи толщиной d₂ = 1 мм с коэффициентом теплопроводности l₂ = 0,08 Вт/ (м×К)? Все другие условия остаются без изменений. Расчет произвести по формуле для плоской стенки и сравнить с соответствующим вариантом задачи 1-37.

Ответ. Тепловая производительность воздухоподогревателя при этих условиях Q = 587 кВт. Снижение производительности D Q = 16,7%. Расход воздуха составит G = 2,23 кг/с.

1-39. Трубопровод диаметром d ₁/ d ₂ = 44/51 мм, по которому течет масло, покрыт слоем бетона толщиной d₂ = 80 мм. Коэффициент теплопроводности материала трубопровода l₁ = 50 Вт/ (м×К); коэффициент теплопроводности бетона l₂ = 1,28 Вт/ (м×К). Средняя температура масла на рассматриваемом участке трубопровода t _ж1 = 1200 °С, температура окружающего воздуха t _ж2 = 20 °С Коэффициент теплоотдачи от масла к стенке a₁ = 100 Вт/ (м²×К) и от поверхности бетона к воздуху a₂ = 10 Вт/ (м²×К).

а) Определить потери теплоты с 1 м оголенного трубопровода и с трубопровода, покрытого бетоном.

б) Каким должен быть коэффициент теплопроводности изоляции, чтобы при любой ее толщине тепловые потери с 1 м изолированной трубы были не больше, чем для оголенного трубопровода?

Ответ.

а) Потери теплоты с единицы длины оголенного трубопровода q_l = 142,5 Вт/м. Потери теплоты трубопровода, покрытого бетоном q_l = 249 Вт/м.

б) Чтобы потери теплоты для изолированного трубопровода были меньше, чем для оголенного, при любой толщине слоя изоляции, необходимо, чтобы l_из 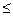0,26 Вт/ (м×К).

1-40. Какой должна быть толщина изоляции из совелита d_из с коэффициентом теплопроводности l_из = 0,08 Вт/ (м×К), чтобы потери теплоты с 1 м изолированного трубопровода были в 3 раза меньше, чем для трубопровода без изоляции, при условиях задачи 1-39?

Ответ. Толщина изоляции должна быть d_из = 75 мм.