2015-01-30
745
Уравнения, связывающие независимую переменную, искомую функцию и её производные называются дифференциальными уравнениями (ДУ).
Решить дифференциальное уравнение – это значит, найти множество функций, которые удовлетворяют данному уравнению. Такое множество функций называется общим решением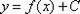 
дифференциального уравнения.
Если искомая (неизвестная) функция зависит от одной переменной, то ДУ называют обыкновенным; иначе – ДУ в частных производных.
Наивысший порядок производной, входящей в ДУ, называется порядком этого уравнения.
Например, уравнение у'''- 3у'' + 2у = 0 - обыкновенное ДУ третьего порядка, а уравнение х2у' + 5ху = у2 - ДУ первого порядка. у· z'x = x·z'х – ДУ в частных производных.
Процесс отыскания решения ДУ называется его интегрированием, а график решения ДУ – интегральной кривой.
