Общий вид ДУ первого порядка: F (x;y;y') = 0 
Дифференциальное уравнение первого порядка, содержит:
1) независимую переменную  ;
;
2) зависимую переменную  (функцию);
(функцию);
3) первую производную функции: 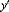 .
.
Если общее уравнение можно разрешить относительно переменной 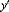 , то его записывают в виде:
, то его записывают в виде:
· = f(x,y) - называют ДУ первого порядка, разрешённым относительно производной.
Это уравнение устанавливает зависимость между координатами точки (x,y) и угловым коэффициентом 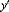 касательной к интегральной кривой, проходящей через эту точку.
касательной к интегральной кривой, проходящей через эту точку.
Т.о. Геометрический смысл ДУ первого порядка: 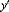 = f(x,y) – даёт совокупность направлений (поле направлений) на плоскости О ху.
= f(x,y) – даёт совокупность направлений (поле направлений) на плоскости О ху.
ДУ первого порядка, разрешённое относительно производной, можно записать в дифференциальной форме: Р(х;у) dx + Q (х;у) dy = 0, где Р(х;у), Q (х;у) – известные функции.
Данное уравнение удобно тем, что переменные х и у в нём равноправны., т.е. любую из них можно рассматривать как функцию другой. Т.о. можно перейти от одного вида записи ДУ к другому.
Интегрирование ДУ в общем случае приводит к бесконечному множеству решений (отличающихся друг от друга постоянными величинами.)Например, решением уравнения 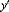 = 2х является функция
= 2х является функция
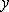 = х 2, а также
= х 2, а также 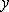 = х 2 + 1,
= х 2 + 1, 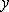 = х 2 -
= х 2 - 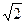 и вообще,
и вообще, 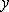 = х 2 + С,, где С – const.
= х 2 + С,, где С – const.
Поэтому, чтобы решение ДУ имело смысл, его надо подчинить некоторым дополнительным условиям.
Условие, что при х = х0 функция 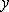 должна быть равна заданному числу
должна быть равна заданному числу 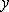 0 называется начальным условием.
0 называется начальным условием.
Начальное условие записывается в виде 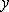 (х0) =
(х0) = 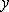 0 или
0 или 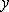 | х = х0 =
| х = х0 = 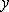 0
0
Общим решением ДУ первого порядка называется функция 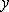 = j(х,С), содержащя одну произвольную постоянную и удовлетворяющая условиям:
= j(х,С), содержащя одну произвольную постоянную и удовлетворяющая условиям:
- Функция j(х, С) является решением ДУ при каждом фиксированном значении С.
- Каково бы ни было начальное условие, можно найти такое значение постоянной С= С0, что функция
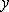 = j(х, С0), удовлетворяет данному начальному условию.
= j(х, С0), удовлетворяет данному начальному условию.
Частным решением ДУ первого порядка называется функция 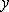 = j(х,С0), полученная из общего решения
= j(х,С0), полученная из общего решения 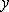 = j(х,С), при конкретном значении постоянной С= С0.
= j(х,С), при конкретном значении постоянной С= С0.
Если общее решение ДУ найдено в неявном виде, т.е. в виде уравнения Ф (х, у, С) = 0, то такое решение называется общим интегралом ДУ.
Уравнение Ф (х, у, С) = 0 в этом случае называется частным интегралом уравнения.
С геометрической точки зрения j(х,С) есть семейство интегральных кривых на плоскости Оху, частное решение 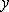 = j(х, С0) - одна кривая из этого семейства, проходящая через точку (х0,у0.).
= j(х, С0) - одна кривая из этого семейства, проходящая через точку (х0,у0.).
Задача отыскания решения ДУ первого порядка, удовлетворяющего заданному начальному условию, называется задачей Коши.
Теорема (существования и единственности решения задачи Коши). Если в уравнении 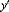 = f(x,y) функция f(x,y) и её частная производная fу¢(x,y) непрерывны в некоторой области D, содержащей точку (х0,у0.), то существует единственное решение у = j(х,) этого уравнения, удовлетворяющее начальному условию
= f(x,y) функция f(x,y) и её частная производная fу¢(x,y) непрерывны в некоторой области D, содержащей точку (х0,у0.), то существует единственное решение у = j(х,) этого уравнения, удовлетворяющее начальному условию 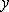 (х0) =
(х0) = 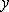 0 или
0 или 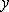 | х = х0 =
| х = х0 = 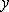 0
0
 2015-01-30
2015-01-30 1352
1352
