● Закон распределения случайной величины
43. Случайная величина  принимает только целые значения
принимает только целые значения 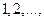
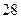 . При этом вероятности возможных значений
. При этом вероятности возможных значений  пропорциональны значениям:
пропорциональны значениям: 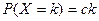 . Найдите значение константы
. Найдите значение константы 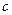 и вероятность
и вероятность 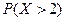 .
.
44. Случайная величина  принимает только целые неотрицательные значения
принимает только целые неотрицательные значения 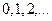 . При этом
. При этом 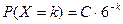 . Найдите значение константы
. Найдите значение константы 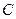 и вероятность
и вероятность 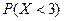 .
.
● Независимые дискретные случайные величины
45. Независимые дискретные случайные величины 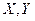 принимают только целые значения:
принимают только целые значения:  – от
– от 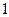 до
до 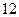 с вероятностью
с вероятностью 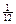 ,
, 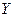 – от
– от  до
до  с вероятностью
с вероятностью 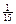 . Найдите вероятность
. Найдите вероятность 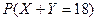 .
.
46. Независимые случайные величины 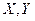 принимают только целые значения:
принимают только целые значения:  – от
– от 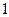 до
до 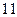 с вероятностью
с вероятностью 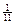 ,
, 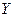 – от
– от 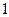 до
до 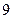 с вероятностью
с вероятностью 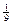 . Найдите вероятность
. Найдите вероятность 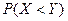 .
.
47. Независимые случайные величины 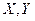 принимают только целые значения:
принимают только целые значения:  – от
– от 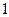 до
до 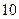 с вероятностью
с вероятностью 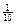 ,
, 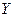 – от
– от 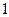 до
до 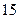 с вероятностью
с вероятностью 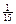 . Найдите вероятность
. Найдите вероятность 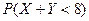 .
.
48. Независимые случайные величины 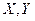 принимают только целые значения:
принимают только целые значения:  – от
– от 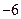 до
до 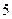 с вероятностью
с вероятностью 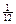 ,
, 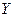 – от
– от 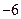 до
до 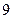 с вероятностью
с вероятностью 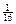 . Найдите вероятность
. Найдите вероятность 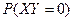 .
.
49. Независимые случайные величины  и
и 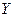 принимают только целые значения:
принимают только целые значения:  – от
– от 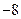 до
до 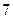 ,
, 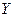 – от
– от 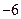 до
до 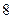 . Найдите
. Найдите 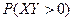 , если известно, что возможные значения
, если известно, что возможные значения  и
и 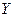 равновероятны.
равновероятны.
50. Независимые случайные величины 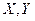 принимают только целые значения:
принимают только целые значения:  – от
– от 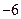 до
до 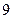 с вероятностью
с вероятностью 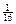 ,
, 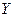 – от
– от 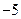 до
до 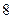 с вероятностью
с вероятностью 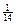 . Найдите
. Найдите 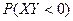 .
.
51. Независимые случайные величины 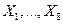 принимают только целые значения от
принимают только целые значения от 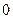 до
до 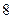 . Найдите вероятность
. Найдите вероятность 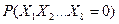 , если известно, что все возможные значения равновероятны.
, если известно, что все возможные значения равновероятны.
52. Независимые случайные величины 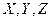 принимают только целые значения:
принимают только целые значения:  – от
– от 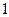 до
до 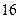 с вероятностью
с вероятностью 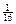 ,
, 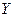 – от
– от 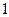 до
до 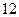 с вероятностью
с вероятностью 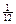 ,
, 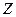 – от
– от 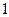 до
до 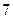 с вероятностью
с вероятностью 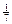 . Найдите вероятность того, что
. Найдите вероятность того, что 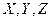 примут разные значения.
примут разные значения.
53. Независимые случайные величины 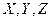 принимают только целые значения:
принимают только целые значения:  – от
– от 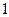 до
до 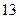 с вероятностью
с вероятностью 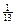 ,
, 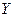 – от
– от 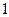 до
до 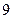 с вероятностью
с вероятностью 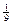 ,
, 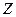 – от
– от 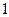 до
до 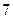 с вероятностью
с вероятностью 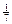 . Найдите вероятность
. Найдите вероятность 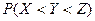 .
.
● Математическое ожидание и дисперсия дискретной случайной величины
54. Распределение дискретной случайной величины  задано таблицей
задано таблицей
 | 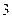 | 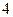 | 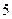 |
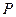 | 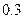 | 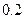 | 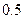 |
Найдите математическое ожидание 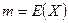 и вероятность
и вероятность 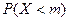 .
.
55. Дискретная случайная величина  принимает только целые значения
принимает только целые значения 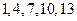 , каждое с вероятностью
, каждое с вероятностью 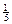 . Найдите математическое ожидание
. Найдите математическое ожидание 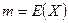 и вероятность
и вероятность 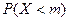 .
.
56. Распределение дискретной случайной величины  задано таблицей
задано таблицей
 | 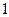 | 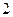 | 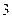 |
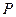 | 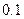 | 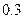 | 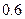 |
Найдите дисперсию 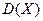 .
.
57. Распределение случайной величины  задано таблицей
задано таблицей
 | 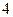 | 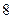 | 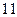 | 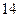 | 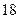 |
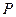 | 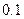 | 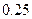 | 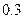 | 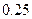 | 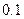 |
Найдите математическое ожидание 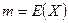 , среднее квадратичное отклонение
, среднее квадратичное отклонение 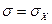 и вероятность
и вероятность 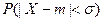 .
.
58. Для случайной величины  известно, что
известно, что 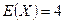 ,
, 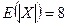 ,
, 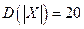 .
.  Найдите дисперсию
Найдите дисперсию 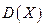 .
.
59. Независимые дискретные случайные величины 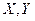 могут принимать только значения
могут принимать только значения 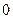 и
и 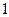 . При этом
. При этом 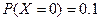 ,
, 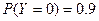 . Найдите математическое ожидание
. Найдите математическое ожидание 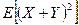 .
.
60. Независимые дискретные случайные величины 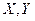 могут принимать только значения
могут принимать только значения 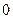 и
и 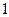 . При этом
. При этом 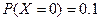 ,
, 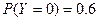 . Найдите математическое ожидание
. Найдите математическое ожидание 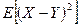 .
.
61. Дискретные случайной величины 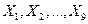 распределены по закону, заданному таблицей
распределены по закону, заданному таблицей
 | 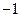 | 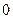 | 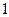 |
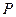 | 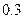 | 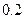 | 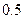 |
Найдите математическое ожидание 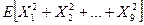 .
.
62. Независимые случайные величины 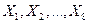 принимают только целые значения
принимают только целые значения 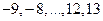 . Найдите математическое ожидание
. Найдите математическое ожидание 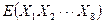 , если известно, что возможные значения равновероятны.
, если известно, что возможные значения равновероятны.
63. Для независимых случайных величин 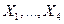 известно, что их математические ожидания
известно, что их математические ожидания 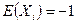 , дисперсии
, дисперсии 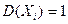 ,
, 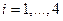 . Найдите дисперсию произведения
. Найдите дисперсию произведения 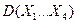 .
.
64. Независимые случайные величины 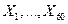 могут принимать только значения
могут принимать только значения 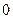 и
и 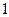 . При этом
. При этом 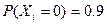 ,
, 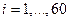 . Найдите математическое ожидание
. Найдите математическое ожидание 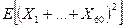 .
.
65. Независимые случайные величины 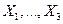 могут принимать только значения
могут принимать только значения 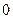 и
и 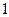 . При этом
. При этом 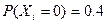 ,
, 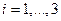 . Найдите математическое ожидание
. Найдите математическое ожидание 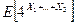 .
.
66. Вероятность выигрыша 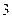 рублей в одной партии равна
рублей в одной партии равна 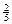 , вероятность проигрыша
, вероятность проигрыша 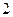 рублей равна
рублей равна 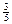 . Найдите дисперсию капитала игрока после
. Найдите дисперсию капитала игрока после 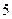 партий.
партий.
● Основные дискретные законы распределения и их характеристики
67. На плоскости начерчены две окружности, радиусы которых 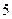 и
и 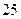 соответственно. Меньшая окружность содержится внутри большего круга. В большой круг наудачу бросаются
соответственно. Меньшая окружность содержится внутри большего круга. В большой круг наудачу бросаются 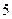 точек. Пусть случайная величина
точек. Пусть случайная величина  – число точек, попавших в малый круг. Вычислите математическое ожидание
– число точек, попавших в малый круг. Вычислите математическое ожидание 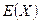 и дисперсию
и дисперсию 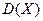 .
.
68. Производится  независимых испытаний, состоящих в том, что одновременно подбрасываются
независимых испытаний, состоящих в том, что одновременно подбрасываются  монет. Пусть
монет. Пусть  – число испытаний, в которых выпало
– число испытаний, в которых выпало 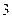 герба. Найдите математическое ожидание
герба. Найдите математическое ожидание 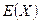 .
.
69. Случайные величины 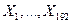 распределены по биномиальному закону с параметрами
распределены по биномиальному закону с параметрами 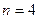 и
и 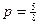 . Найдите математическое ожидание
. Найдите математическое ожидание 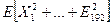 .
.
70. Случайные величины 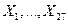 независимы и распределены по биномиальному закону с параметрами
независимы и распределены по биномиальному закону с параметрами 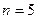 и
и 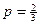 . Найдите математическое ожидание
. Найдите математическое ожидание 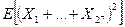 .
.
71. Отрезок длины 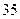 поделен на две части длины
поделен на две части длины 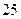 и
и 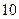 соответственно.
соответственно. 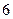 точек последовательно бросаются наудачу на отрезок.
точек последовательно бросаются наудачу на отрезок.  – случайная величина, равная числу точек, попавших на отрезок длины
– случайная величина, равная числу точек, попавших на отрезок длины 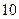 . Найдите математическое ожидание и среднее квадратичное отклонение величины
. Найдите математическое ожидание и среднее квадратичное отклонение величины  .
.
72. Производится 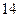 независимых испытаний, в каждом из которых подбрасываются
независимых испытаний, в каждом из которых подбрасываются 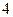 игральные кости. Пусть
игральные кости. Пусть  – число испытаний, в которых все выпавшие цифры оказались
– число испытаний, в которых все выпавшие цифры оказались 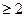 . Найдите дисперсию
. Найдите дисперсию 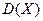 .
.
73. Производится 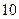 независимых испытаний с вероятностью успеха
независимых испытаний с вероятностью успеха 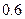 в каждом испытании. Пусть
в каждом испытании. Пусть  – число успехов в испытаниях с номерами
– число успехов в испытаниях с номерами 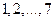 ,
, 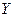 – число успехов в испытаниях с номерами
– число успехов в испытаниях с номерами 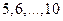 . Найдите дисперсию
. Найдите дисперсию 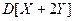 .
.
74. На плоскости начерчены два квадрата, стороны которых 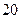 и
и 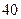 соответственно. Меньший квадрат содержится внутри большего квадрата. В большой квадрат случайным образом бросают точки до тех пор, пока не попадут в маленький квадрат. Пусть случайная величина
соответственно. Меньший квадрат содержится внутри большего квадрата. В большой квадрат случайным образом бросают точки до тех пор, пока не попадут в маленький квадрат. Пусть случайная величина  – число бросаний. Найдите математическое ожидание
– число бросаний. Найдите математическое ожидание 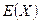 и дисперсию
и дисперсию 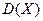 .
.
75. В спортивной лотерее каждую неделю на 100 билетов разыгрывается 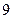 палаток и
палаток и 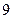 рюкзаков. Турист решил каждую неделю покупать по одному билету до тех пор, пока он не выиграет палатку и рюкзак. Найдите среднее время реализации данного намерения (время измеряется в неделях).
рюкзаков. Турист решил каждую неделю покупать по одному билету до тех пор, пока он не выиграет палатку и рюкзак. Найдите среднее время реализации данного намерения (время измеряется в неделях).
76. В серии независимых испытаний, которые проводятся с частотой одно испытание в единицу времени, вероятность наступления события 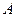 в одном испытании равна
в одном испытании равна 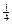 . Пусть
. Пусть 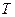 – время ожидания наступления события
– время ожидания наступления события 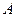
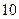 раз (за все время ожидания). Найдите математическое ожидание
раз (за все время ожидания). Найдите математическое ожидание 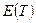
 и дисперсию
и дисперсию 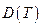 .
.
77. Случайные величины 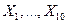 распределены по геометрическому закону с одинаковым математическим ожиданием, равным
распределены по геометрическому закону с одинаковым математическим ожиданием, равным 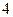 . Найдите математическое ожидание
. Найдите математическое ожидание 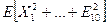 .
.
78. Случайные величины независимы 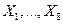 и распределены по геометрическому закону с одинаковым математическим ожиданием, равным
и распределены по геометрическому закону с одинаковым математическим ожиданием, равным 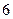 . Найдите математическое ожидание
. Найдите математическое ожидание 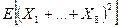 .
.
79. Случайные величины 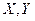 распределены по геометрическому закону. Найдите дисперсию
распределены по геометрическому закону. Найдите дисперсию 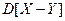 , если их математические ожидания равны
, если их математические ожидания равны 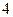 , а коэффициент корреляции
, а коэффициент корреляции  и
и 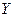 равен
равен 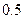 .
.
80. Случайная составляющая выручки равна 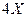 , где
, где  – биномиальная случайная величина с параметрами
– биномиальная случайная величина с параметрами 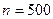 и
и 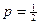 . Случайная составляющая затрат имеет вид
. Случайная составляющая затрат имеет вид 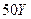 , где
, где 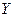 – пуассоновская случайная величина. Найдите дисперсию прибыли, считая, что
– пуассоновская случайная величина. Найдите дисперсию прибыли, считая, что  и
и 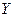 – независимы, а
– независимы, а 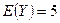 .
.
81. Для пуассоновской случайной величины  отношение
отношение 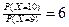 . Найдите математическое ожидание
. Найдите математическое ожидание 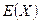 .
.
● Ковариация и коэффициент корреляции
82. Даны математические ожидания случайных величин  и
и 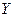 :
: 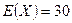 ,
, 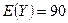 , их дисперсии
, их дисперсии 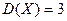 ,
, 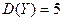 и ковариация Cov
и ковариация Cov 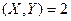 . Найдите математическое ожидание
. Найдите математическое ожидание 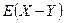 и дисперсию
и дисперсию 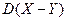 .
.
83. Случайные величины 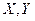 принимают только значения
принимают только значения 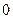 и
и 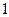 . Найдите дисперсию
. Найдите дисперсию 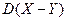 , если вероятности
, если вероятности 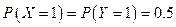 , а коэффициент корреляции
, а коэффициент корреляции  и
и 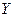 равен
равен 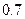 .
.
84. Для случайных величин 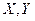 даны их математические ожидания и дисперсии
даны их математические ожидания и дисперсии 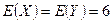 ,
, 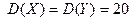 , а также коэффициент корреляции
, а также коэффициент корреляции 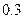 . Найдите математическое ожидание
. Найдите математическое ожидание 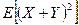 .
.
85. Случайные величины 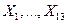 распределены по закону Пуассона с одинаковым математическим ожиданием, равным
распределены по закону Пуассона с одинаковым математическим ожиданием, равным 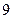 . Найдите математическое ожидание
. Найдите математическое ожидание 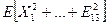 .
.
86. Случайные величины 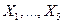 независимы и распределены по закону Пуассона с одинаковым математическим ожиданием, равным
независимы и распределены по закону Пуассона с одинаковым математическим ожиданием, равным 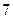 . Найдите математическое ожидание
. Найдите математическое ожидание 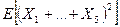 .
.
87. Случайные величины 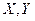 распределены по закону Пуассона. Найдите
распределены по закону Пуассона. Найдите 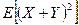 , если
, если 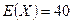 и
и 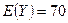 , а коэффициент корреляции
, а коэффициент корреляции  и
и 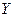 равен
равен 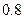 .
.
 2015-01-07
2015-01-07 1582
1582
