Занятие 1.
Основные понятия теории вероятностей. Классическое определение вероятности. Элементы комбинаторики. Непосредственный подсчет вероятности.
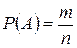 — формула непосредственного подсчета вероятности.
— формула непосредственного подсчета вероятности.
A – случайное событие.
P(A) - вероятность случайного события А.
n – число элементарных событий рассматриваемого опыта.
m - число элементарных событий рассматриваемого опыта, благоприятствующих событию А.
Задача 1.
Кубик, все грани которого окрашены, распилен так, что каждое его ребро разделено на 10 частей. Из полученного множества кубиков на удачу выбирается один. Какова вероятность того, что у него окрашены: 1) 3 грани (событие А); 2) 2 грани (событие B); 3) 1 грань (событие C); 4) ни одной грани (событие D); 5) хотя бы одна грань (событие E); 6) 4 грани (событие F); 7) не меньше двух граней (событие G).
Решение.
 Для рассматриваемой задачи элементарным событием является событие, состоящее в появлении одного конкретного маленького кубика, потому что:
Для рассматриваемой задачи элементарным событием является событие, состоящее в появлении одного конкретного маленького кубика, потому что:
· в результате опыта, хотя бы один кубик будет выбран обязательно (следовательно, события образуют полную группу)
· никакие два кубика не могут появиться одновременно (следовательно, события попарно несовместные)
· у нас нет объективных причин считать, что какие-либо кубики в результате выбора будут появляться чаще, чем другие (события равно возможны)
Таким образом число элементарных событий для данной задачи равно числу маленьких кубиков, полученных после того, как был распилен большой кубик.
n=1000
1) Определим вероятность события A. Число элементарных событий, благоприятствующих событию А равно числу кубиков с тремя окрашенными гранями, а таких кубиков столько, сколько вершин у куба, т. е. 8.
mA=8
P(A)=mA/n P(A)=8/1000
Определим вероятности остальных событий, указанных в задаче:
2) mB=8 . 12=96 P(B)=mB/n P(B)=96/1000
3) mC=8 . 8 . 6=384 P(B)=mC/n P(C)=384/1000
4) mD=8 . 8 . 8 . =512 P(D)=mD/n P(D)=512/1000
5) mE=8+96+384=488 P(E)=mE/n P(E)=488/1000
6) mF=0 P(F)=mF/n P(F)=0
7) mG=96+8=104 P(G)=mG/n P(G)=104/1000
Задача 2.
Брошены 2 монеты. Найти вероятность того, что:
1) на одной монете выпадет «герб» (событие А);
2) хотя бы на одной монете выпадет «герб» (событие B).
Решение.
Рассмотрим события:
1) На первой монете выпал «герб» и на второй монете выпал «герб»
2) На первой монете выпал «герб», а на второй монете выпала «цифра»
3) На первой монете выпала «цифра», а на второй монете выпал «герб»
4) На первой монете выпала «цифра» и на второй монете выпала «цифра»
В результате опыта обязательно произойдет, хотя бы одно из перечисленных событий, значит, они образуют полную группу. Никакие из двух событий не могут произойти одновременно, значит, они попарно несовместные. Нет оснований считать, что какое-либо из событий будет происходить чаще, чем другие, значит, они равно вероятные. Таким образом рассмотренные события образуют множество элементарных событий опыта. n=4.
Определим вероятность события А. Благоприятствующими ему будут второе и третье из приведенного списка. mA=2.
P(A)=mA/n P(A)=2/4=0.5
Определим вероятность события B. Благоприятствующими ему будут первое, второе и третье из приведенного списка. mB=3.
P(A)=mB/n P(B)=3/4=0.75
Задача 3.
Брошены два игральных кубика. Определить вероятность того, что:
1) сумма выпавших очков равна 7 (событие А);
2) разность выпавших очков равна 3 (событие B);
3) сумма выпавших очков равна 7, а разность равна 3 (событие C);
4) сумма выпавших очков равна 7, если известно, что разность равна 3 (событие D);
Решение.
Рассмотрим комбинацию двух чисел (k,r), где k и r могут принимать значения от 1 до 6. В результате опыта всегда появляется, хотя бы одна такая комбинация (события образуют полную группу), никакие две комбинации не могут появиться одновременно (события попарно несовместные), нет оснований считать, что какие-либо из комбинаций будут появляться чаще, чем другие (события равно вероятные). Таким образом множество комбинаций чисел (k,r) образует пространство элементарных событий. Количество таких комбинаций равно n=36.
1) Благоприятствующими для события А являются комбинации: (1,6), (2,5), (3,4), (4,3), (5,2), (6,1). mA=6.
P(A)=mA/n P(A)=6/36=1/6.
2) Благоприятствующими для события B являются комбинации: (1,4), (2,5), (3,6), (4,1), (5,2), (6,3). mB=6.
P(B)=mB/n P(B)=6/36=1/6.
3) Благоприятствующими для события C являются комбинации: (2,5), (5,2). mC=2.
P(C)=mC/n P(C)=2/36=1/18.
4) Так как известно, что в результате опыта уже выпала комбинация чисел, разность которых равна 3, то множество элементарных событий образуют только такие комбинации: (1,4), (2,5), (3,6), (4,1), (5,2), (6,3).
В этом случае n=6.
Благоприятствующими для события D являются комбинации: (2,5), (5,2). mD=2.
P(D)=mD/n P(D)=2/6=1/3.
Задача 4.
На 5 карточках написаны буквы о, п, р, с, т. Какова вероятность события А, состоящего в том, что, вынимая карточки по одной и, раскладывая их в порядке выхода, получим слово «спорт».
Решение.
Множество элементарных событий данного опыта образуют все возможные перестановки из пяти букв. Количество таких перестановок Р5=5!
Следовательно, n=5!=1 . 2 . 3 . 4 . 5=120.
Благоприятствующим событию А является только одна перестановка «спорт».
mA=1.
P(A)=mA/n P(A)=1/120
Задача 5.
На 6 карточках написаны буквы к, л, м, о, о, о. Какова вероятность события А, состоящего в том, что, вынимая карточки по одной и, раскладывая их в порядке выхода, получим слово «молоко».
Решение.
Множество элементарных событий данного опыта образуют все возможные перестановки из шести букв (считаем, что буквы о отличными друг от друга, и обозначим их о1, о2, о3). Количество таких перестановок Р6=6!
Следовательно, n=6!=1 . 2 . 3 . 4 . 5 . 6=720.
Благоприятствующим событию А являются перестановки:
мо1ло2ко3, мо1ло3ко2, мо2ло1ко3, мо2ло3ко1, мо3ло1ко2, мо3ло2ко1.
Количество таких перестановок равно количеству перестановок букв о между собой и равно Р3=3!=6
mA=6.
P(A)=mA/n P(A)=6/720=1/120
Задача 6.
На карточках написаны цифры 1,2,3,4,5,6,7. По одной вынимается три карточки. Какова вероятность того, что:
1) В порядке выхода цифр появится число 234 (событие А);
2) Из полученных цифр можно будет составить число 234 (событие В);
3) Можно будет составить число 525 (событие С).
Решение.
1) Множество элементарных событий данного опыта образуют все возможные размещения из семи цифр по три. Количество таких размещений
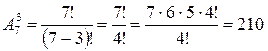
Следовательно, n=210.
благоприятствующим является только одно размещение 234. mА=1.
P(A)=mA/n P(A)=1/210
2) Множество элементарных событий данного опыта образуют все возможные сочетания из семи цифр по три. Количество таких сочетаний
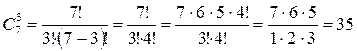
Следовательно, n=35.
благоприятствующим является только одно сочетание, содержащее, цифры 2, 3, 4. mА=1.
P(A)=mA/n P(A)=1/35
3) Множество элементарных событий данного опыта образуют также все возможные сочетания из семи цифр по три. Следовательно, n=35.
Число благоприятствующих событий равно 0, так как цифра 5 не может появиться дважды ни в одном сочетании. mD=0.
P(D)=mD/n P(D)=0
Событие D есть событие невозможное.
Задача 7.
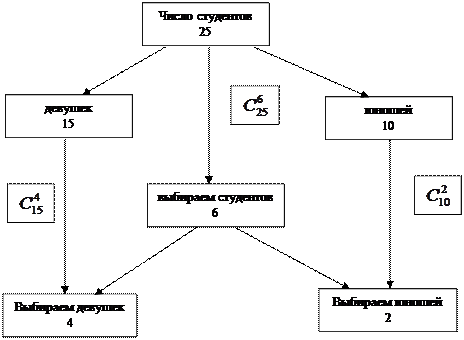
В группе 25 студентов, из них 15 девушек. Какова вероятность того, что среди первых 6 вошедших в аудиторию будет 4 девушки?
Решение.
Обозначим: А – событие, состоящее в том, что среди первых 6 вошедших в аудиторию оказалось 4 девушки.
Множество элементарных событий данного опыта образуют все возможные сочетания из 25 студентов по шесть. n= 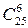 .
.
Благоприятствующими событию А являются все сочетания содержащие 4 девушки. Такое сочетание можно получить, если к любому сочетанию четырех девушек, выбранных из 15, добавить любое сочетание двух юношей, выбранных из 10. Число сочетаний четырех девушек, выбираемых из 15 равно 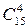 , а число сочетаний двух юношей, выбираемых из 10 равно
, а число сочетаний двух юношей, выбираемых из 10 равно 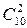 . Тогда число благоприятствующих событию А сочетаний равно mA=
. Тогда число благоприятствующих событию А сочетаний равно mA= 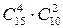
P(A)=mA/n
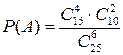
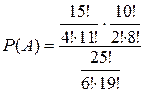
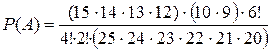
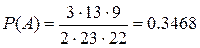
 |
Контрольные вопросы:
1. Предмет теории вероятностей.
2. Достоверное событие.
3. Невозможное событие.
4. Случайное событие.
5. Совместные и несовместные события.
6. Полная группа событий.
7. Равновозможные события.
8. Элементарное событие.
9. Благоприятствующие события.
10. Классическое определение вероятности. Формула непосредственного подсчета вероятностей.
11. Размещения. Определение и формула для подсчета числа размещений.
12. Перестановки. Определение и формула для подсчета числа перестановок.
13. Сочетание. Определение и формула для подсчета числа сочетаний.
 2015-02-24
2015-02-24 865
865







