Формула полной вероятности. Формула Бейеса. Повторение испытаний.
Задача 1.
В лаборатории имеются шесть компьютеров первого типа и четыре компьютера второго типа. Вероятность того, что за время выполнения некоторого расчета компьютер первого типа не выйдет из строя, равна 0.95, для компьютера второго типа эта вероятность равна 0.9. Студент производит расчет на случайно выбранной машине. Найти вероятность того,что до окончания расчета машина не выйдет из строя.
Решение.
Обозначим события:
А-до окончания расчета компьютер не выйдет из строя;
В1-расчет производится на компьютере первого типа;
В2- расчет производится на компьютере второго типа;
События В1 и В2 несовместные и образуют полную группу. Событие А всегда происходит одновременно с одним из событий В1 или В2. Поэтому события В1 и В2 можем принять в качестве гипотез и для вычисления вероятности события А применить формулу полной вероятности.
Р(А)=Р(В1)Р(А/В1)+Р(В2)Р(А/В2)
Вероятность выбора для расчета компьютера первого типа очевидно, равна
Р(В1)=6/10, для компьютера второго типа эта вероятность будет Р(В2)=4/10.
Из условия задачи также понятно, что Р(А/В1)=0.95, а Р(А/В2)=0.9.
В итоге получаем:
Р(А)=0.6 . 0.95+0.4 . 0.9=0.93
Ответ: вероятность того,что до окончания расчета случайно выбранная машина не выйдет из строя равна 0.93.
Задача 2.
На склад поступает продукция трех фабрик, причем продукция первой фабрики составляет 20%, второй – 46%, третьей – 34%. Известно, что средний процент нестандартных деталей для первой фабрики равен – 3%, второй – 2%, третьей – 1%. Найти вероятность того, что на удачу взятое изделие произведено на первой фабрике, если оно оказалось стандартным.
Решение.
Обозначим события:
А – взятое изделие оказалось стандартным;
В1-изделие произведено на первой фабрике;
В2- изделие произведено на второй фабрике;
В3- изделие произведено на третьей фабрике;
Нам необходимо определить условную вероятность события В1, если событие А произошло, т. е. величину Р(В1/А).
События В1, В2 и В3 несовместны и образуют полную группу. Событие А всегда происходит одновременно с одним из событий В1, В2 или В3. Поэтому события В1, В2 и В3 можем принять в качестве гипотез и для вычисления вероятности Р(В1/А) применить формулу Бейеса.
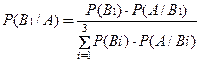
Из условия задачи находим
Р(В1)=0.2; Р(В2)=0.46; Р(В3)=0.34;
Для каждой фабрики нам известен средний процент нестандартных деталей, значит, отняв эту величину от 100% мы можем вычислить средний процент стандартных деталей. Перейдя от процентов к десятичной дроби, мы получим условные вероятности события А в случае,если произошли соответственно события В1, В2, В3.
Р(А/В1)=1-0.3=0.97; Р(А/В2)=1-0.2=0.98; Р(А/В3)=1-0.1=0.99
Теперь можем вычислить величину Р(В1/А):
Р(В1/А)=(0.2 . 0.97)/(0.2 . 0.97+0.46 . 0.98+0.34 . 0.99)
Р(В1/А)=0.1977
Ответ: вероятность того, что наудачу взятое изделие произведено на первой фабрике, если оно оказалось стандартным равна 0.1977.
Задача 3.
Игральная кость брошена пять раз. Определить вероятность того, что шесть очков выпадет три раза.
Решение.
Для данной задачи опытом является бросание игральной кости. Таких опытов производится шесть. В каждом из опытов может произойти событие А, состоящее в выпадении шести очков. Опыты независимы, так как вероятность события А в любом из опытов не зависит от результатов других. Вероятность события А в каждом из опытов одинакова и равна 1/6. Следовательно, для решения задачи мы можем воспользоваться формулой Бернулли.
Количество независимых опытов n=5.
Количество опытов, в которых событие А произойдет интересующее нас число раз m=3.
Вероятность события А в одном опыте р=1/6.
Р5(3)=С53(1/6)3(1-1/6)2= 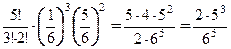 =0.032
=0.032
Ответ:вероятность того, что шесть очков выпадет три раза равна 0.032.
Задача 4.
Вероятность того, что пассажир опоздает на поезд равна 0.02. Найти найвероятнейшее число опоздавших из 855 пассажиров.
Решение.
Число опытов n равно числу пассажиров, желающих уехать. Опыты независимы, так как вероятность опоздать для каждого пассажира не зависит от того опоздают или нет другие пассажиры, и эта вероятность равна 0.02. Поэтому для определения найвероятнейшего числа опоздавших пассажиров k0 можем воспользоваться формулой:
np-q≤k0≤np+p
n=855 p=0.02 q=1-p q=1-0.02=0.98
855 . 0.02-0.98≤k0≤855 . 0.02+0.02
16.12≤k0≤17.12
k0 – целое число, следовательно, k0=17.
Ответ:найвероятнейшее число опоздавших из 855 пассажиров равно 17
Задача 5.
Вероятность поражения мишени при одном выстреле 0.8. Найти вероятность того, что при 100 выстрелах мишень будет поражена:
1) 75 раз;
2) не менее 75 раз.
Решение.
По условию задачи производится 100 независимых опытов (выстрелов по мишени). В каждом из которых может произойти событие (поражение мишени), вероятность которого не зависит от исходов остальных опытов. Таким образом опыты независимы. Так как число опытов велико, то для решения задачи следует воспользоваться локальной и интегральной теоремами Лапласа.
1) Используем локальную теорему Лапласа. Вероятность того, что при n опытах событие произойдет m раз определяется о формуле Pn(m)=φ(x)/√(npq), где
x=(m-np)/√(npq) q=1-p
n=100 m=75 p=0.8 q=1-0.8=0.2
√(npq) =√(100 . 0.8 . 0.2)=4 x=(75-100.0.8)/4=-1.25
По таблице находим
φ(-1.25)=φ(1.25)=0.1826
P100(75)=0.1826/4=0.04565
2) Используем интегральную теорему Лапласа. Вероятность того, что при n опытах событие произойдет от k1 до k2 раз определяется о формуле:
Pn(k1,k2)=Φ(x2) - Φ(x1)
x1=(k1-np)/√(npq) x2=(k2-np)/√(npq)
n=100 k1=75 k2=100 p=0.8 q=0.2
x1=(75-100.0.8)/4=-1.25 x2=(100-100.0.8)/4=5
По таблице находим
Φ(-1.25)=-Φ(1.25)=-0.3944 Φ(5)=0.5
P100(75,100)=Φ(5) - Φ(-1.25)=0.5-(-0.3944)=0.8944
Ответ:
1)Вероятность того, что при 100 выстрелах мишень будет поражена 75 раз P100(75)=0.04565
2)Вероятность того, что при 100 выстрелах мишень будет поражена не менее 75 раз P100(75,100)=0.8944
Задача 6.
Было посеяно 29 семян, с одной и той же вероятностью прорасти. Найти эту вероятность, если вероятнее всего прорастет 24.
Решение.
Проведено 29 опытов – посеяно 29 семян. Вероятность прорасти у каждого семени не зависит от того прорастут другие семена или нет, поэтому опыты независимые. Вероятность прорасти для каждого семени одна и та же, обозначим ее p.
Рассмотрим формулу: np-q≤k0≤np+p
 q=1-p n=29 k0=24
q=1-p n=29 k0=24
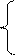
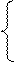 np-q≤k0 np-(1-p)≤k0 (n+1)p-1≤k0 p≤(k0+1)/ (n+1)
np-q≤k0 np-(1-p)≤k0 (n+1)p-1≤k0 p≤(k0+1)/ (n+1)
k0≤np+p k0≤(n+1)p k0≤(n+1)p p≥ k0/(n+1)
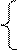
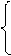 p≤(24+1)/ (29+1) p≤25/30
p≤(24+1)/ (29+1) p≤25/30
p≥ 24/(29+1) p≥ 24/30
Ответ:вероятность всхожести семян (4/5)≤p≤(5/6) или 0.8≤p≤0.83
Контрольные вопросы:
1. Формула полной вероятности.
2. Формула Бейеса.
3. Формула Бернулли.
5. Интегральная теорема Лапласа.
6. Найвероятнейшее число наступления событий.
 2015-02-24
2015-02-24 4015
4015
