2015-02-24
767
Задача 1.
Непрерывная случайная величина задана интегральной функцией распределения
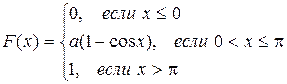
Определить: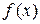 
, значение параметра a, вероятность 
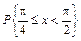, построить графики функций 
.
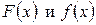Решение.
Функция плотности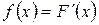 
, следовательно:
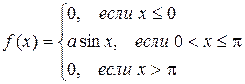
Для определения значения параметра a воспользуемся свойством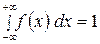 
.
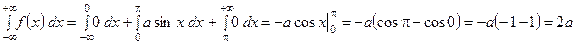
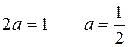
Таким образом, интегральная функция распределения имеет вид:
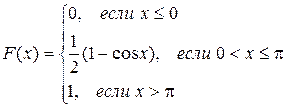
Функция плотности имеет вид:
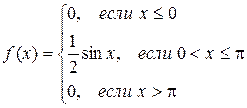
Вероятность попадания случайной величины на заданный отрезок [ a, b ] определяется по формуле: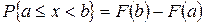 
или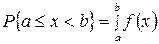 
.
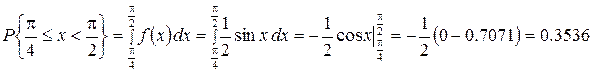
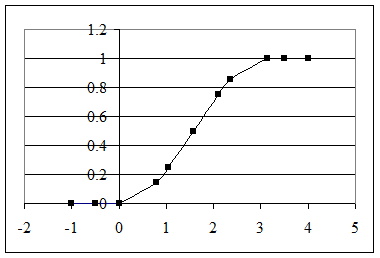
График функции плотности f(x):
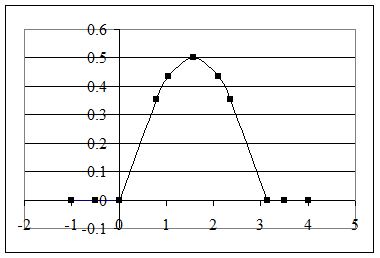
График интегральной функции распределения F(x):
Задача 2.
Непрерывная случайная величина задана плотностью распределения:
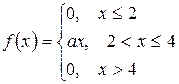
Определить значение параметра a, интегральную функцию распределения F(x), значения mx, Dx, σx, построить графики функций f(x) и F(x).
Решение.
Для определения значения параметра a воспользуемся свойством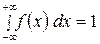 
.
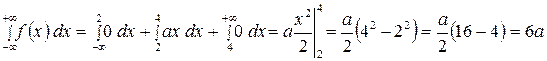
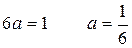
Функция плотности имеет вид:
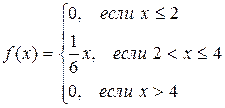
Интегральная функция распределения F(x) определяется по формуле:
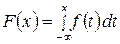
1) 
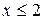
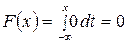
2) 
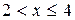
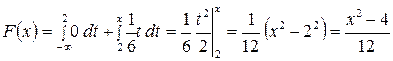
3) 
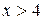
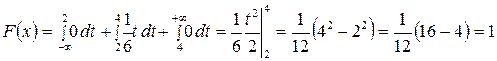
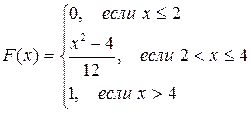
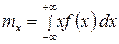
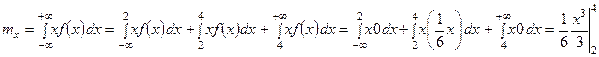
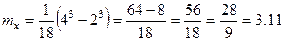
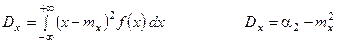
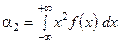
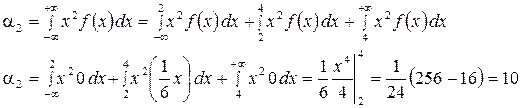
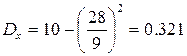
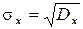
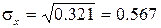
График функции плотности f(x):
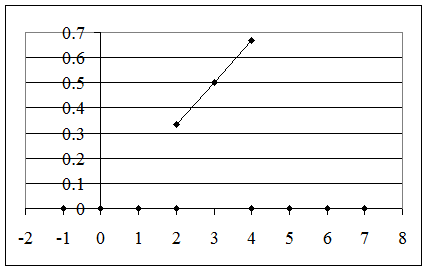
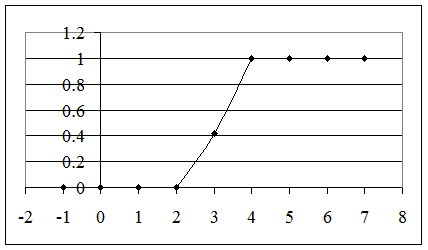
График интегральной функции распределения F(x):
Контрольные вопросы:
1. Определение непрерывной случайной величины.
2. Определение закона распределения случайной величины.
3. Интегральная функция распределения случайной величины. Определение и свойства.
4. Плотность распределения вероятности. Определение и свойства.
5. Вероятность попадания непрерывной случайной величины в заданный интервал.
6. Определение функции распределения по известной плотности распределения.
7. Характеристики положения случайной величины на числовой оси (математическое ожидание, мода, медиана).
8. Начальные и центральные моменты случайных величин. Свойства моментов случайных величин.
9. Равномерный закон распределения случайной величины (дифференциальная и интегральная функции распределения и их графики; числовые характеристики; вероятность попадания случайной величины на заданный участок).
10. Показательный закон распределения (дифференциальная и интегральная функции распределения и их графики; числовые характеристики; вероятность попадания случайной величины на заданный участок).
11. Нормальный закон распределения (дифференциальная и интегральная функции распределения и их графики; числовые характеристики; вероятность попадания случайной величины на заданный участок).
