Гипербола

Эта кривая задается уравнением 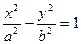. Это уравнение называется каноническим. Чтобы сделать эскиз этой кривой, на оси OX надо отметить точки 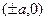, а на оси OY отметить точки 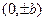. Построить прямоугольник, проходящий через эти точки и пунктиром провести прямые, проходящие через диагонали этого прямоугольника. Эти прямые называются асимптотами гиперболы. Затем вписываются две ветви гиперболы.

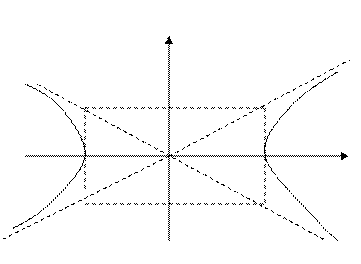
Пример. Выделяя полные квадраты, сделать эскиз гиперболы.

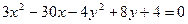
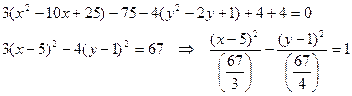
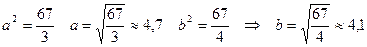центр кривой в точке .

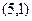Отмечаем центр гиперболы, пунктирными линиями переносим в нее оси координат, строим прямоугольник, проводим в нем диагонали и вписываем две ветви гиперболы.

Заметим, что если получилось уравнение 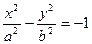, то надо поменять знак:

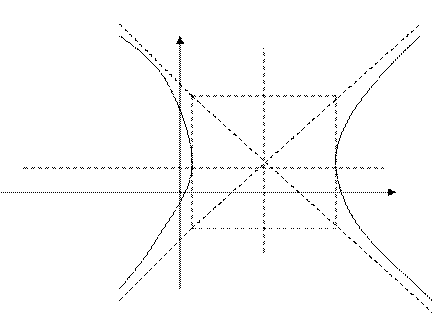
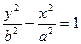. У этой гиперболы ветви направлены не вправо и влево, а вверх и вниз. Строится такая гипербола точно также, только ветви гиперболы вписываются в верхний и нижний угол между асимптотами.