Для функции нескольких переменных можно определить производные от производных, т.е. производные высших порядков.
Для производных второго порядка функции 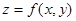 приняты следующие обозначения:
приняты следующие обозначения:
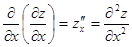 - функция дифференцируется по x последовательно два раза, считая y постоянной величиной;
- функция дифференцируется по x последовательно два раза, считая y постоянной величиной;
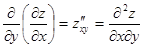 - функция сначала дифференцируется по x, а затем результат дифференцируется по y;
- функция сначала дифференцируется по x, а затем результат дифференцируется по y;
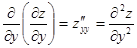 - функция последовательно дифференцируется по y два раза.
- функция последовательно дифференцируется по y два раза.
Следует иметь в виду, что 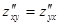 при условии, что они непрерывны. Производные
при условии, что они непрерывны. Производные 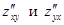 называются смешанными.
называются смешанными.
Аналогично вводятся частные производные 3-го и т.д. порядков.
Полный дифференциал функции 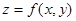 вычисляется по формуле:
вычисляется по формуле: 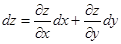 , причем
, причем 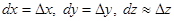 .
.
Пример. Найти полный дифференциал функции 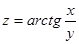 .
.
Решение. 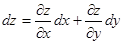 . Найдем частные производные.
. Найдем частные производные.
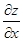 - вычислим производную по x, считая y постоянным.
- вычислим производную по x, считая y постоянным.
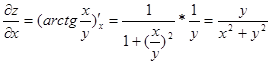 .
.
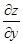 - вычислим производную по y, считая x постоянным.
- вычислим производную по y, считая x постоянным.
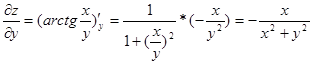 .
.
Тогда 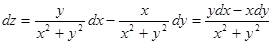 .
.
 2015-02-27
2015-02-27 1280
1280
