Задача 1. Два положительных точечных заряда находятся на расстоянии 0,5 м один от другого. Величина одного заряда вдвое больше другого заряда. На прямой, соединяющей эти заряды, находится третий заряд. Определить, на каком от большего заряда находится третий заряд, если система находится в равновесии?
 Дано: r = 0,5 м; q2= 2q1. Дано: r = 0,5 м; q2= 2q1.  x -? x -? | Решение:              F2 F1 F2 F1     x q1 q3 q2 x q1 q3 q2
Рис. 8 | ||
На заряд q3 действуют силы: F1 и F2 – электрические силы взаимодействия с зарядами q1 и q2 соответственно. Запишем условия равновесия в скалярной форме относительно оси Х: F1 – F2 = 0, откуда F1 = F2. Учитывая, что 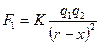 ; ; 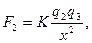 где х – расстояние между зарядами q2 и q3. Получаем где х – расстояние между зарядами q2 и q3. Получаем 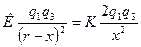 или или 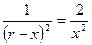 ; откуда х = 1,4(r – x); 2,4x = 1,4r. ; откуда х = 1,4(r – x); 2,4x = 1,4r. 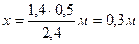 . Ответ: х = 0,3 м. . Ответ: х = 0,3 м. |
Задача 2. Бесконечная вертикальная плоскость заряжена с поверхностной плотностью, равной 10мкКл/м2. К плоскости на шелковой нити подвешен шарик массой 1,5 г. Определить заряд шарика, если нить образует угол 30о с плоскостью.
Дано: 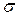 =10мкКл/м2= 10-5 Кл/м2; m = 1,5г = 1,5.10-3 кг; =10мкКл/м2= 10-5 Кл/м2; m = 1,5г = 1,5.10-3 кг; 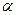 = 30о. = 30о.
q -? |   Решение: Решение: 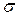 у у   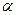 Т Fк х Т Fк х  mg Рис. 9 mg Рис. 9 | |||
На заряженный шарик, подвешенный на нити, в электрическом поле действуют: F – электрическая сила, с которой поле плоскости действует на заряженный шарик, mg – сила тяжести, Т – сила натяжения нити. Запишем условия равновесия шарика относительно осей х и у: Ось х F - Tsin 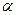 = 0; (1) Ось у -mg + Tcos = 0; (1) Ось у -mg + Tcos 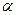 = 0. (2) Решая (1) и (2) получим F = mg tg = 0. (2) Решая (1) и (2) получим F = mg tg 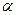 . (3) Учитывая, что F=Eq, a . (3) Учитывая, что F=Eq, a 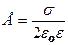 , получим , получим 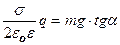 , , 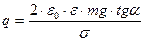 . . 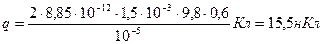 . Ответ: q = 15,5 нКл. . Ответ: q = 15,5 нКл. |
Задача 3. Электрическое поле создано двумя точечными зарядами 2.10-7 Кл и -2.10-7 Кл. Расстояние между зарядами 50 см. Определить напряженность электрического поля в точке А, находящейся на расстоянии 40 см от первого заряда и на расстоянии 30 см от второго заряда.
 Дано: q1 = 2.10-7 Kл; q2 = -2.10-7 Kл; r = 50 cм = 0,5 м; r1 = 40 см = 0,4 м; r2 = 30 см = 0,3 м; Дано: q1 = 2.10-7 Kл; q2 = -2.10-7 Kл; r = 50 cм = 0,5 м; r1 = 40 см = 0,4 м; r2 = 30 см = 0,3 м;  Е -? Е -? | 
  E E
r Рис. 10 | |||||||||
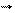 Согласно принципу суперпозиции напряженность Е равна – векторной сумме напряженностей Согласно принципу суперпозиции напряженность Е равна – векторной сумме напряженностей 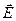 1 и 1 и 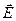 2, т.е. 2, т.е. 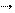 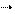 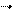 Е = Е1 + Е2. (1) По теореме косинусов Е = Е1 + Е2. (1) По теореме косинусов 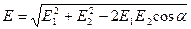 , (2) где , (2) где 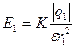 , (3) , (3) 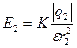 . (4) cos . (4) cos 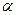 найдем найдем 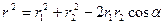 . . 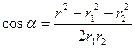 . . 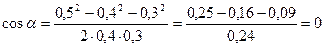 ; следовательно, ; следовательно, 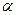 = 900. Уравнение (2) примет вид: = 900. Уравнение (2) примет вид: 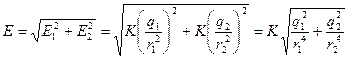 . (5) Подставим численные значения: . (5) Подставим численные значения: 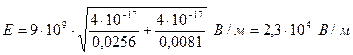 . Ответ: Е = 2,3.104 В/м. Задача 4.Точечный заряд Q=25 нКл находится в поле, созданном прямым бесконечным цилиндром радиусом R=1 cм, равномерно заряженным с поверхностной плотностью σ=2·103 нКл/м2. Определить силу, действующую на заряд, помещенный от оси цилиндра на расстоянии r=10 см. . Ответ: Е = 2,3.104 В/м. Задача 4.Точечный заряд Q=25 нКл находится в поле, созданном прямым бесконечным цилиндром радиусом R=1 cм, равномерно заряженным с поверхностной плотностью σ=2·103 нКл/м2. Определить силу, действующую на заряд, помещенный от оси цилиндра на расстоянии r=10 см.
|
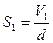 и и 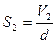 , где , где 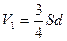 и и 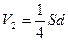 , поэтому , поэтому 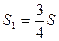 и и 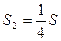 . Общая емкость этой батареи с = с1 + с2, где . Общая емкость этой батареи с = с1 + с2, где 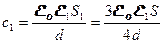 и и 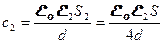 , поэтому , поэтому 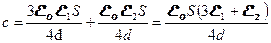 (1) Суммарный заряд на батарее из этих двух конденсаторов остался таким же, каким был до погружения: (1) Суммарный заряд на батарее из этих двух конденсаторов остался таким же, каким был до погружения: 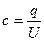 , откуда , откуда 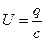 . (2) Подставив (1) в (2) . (2) Подставив (1) в (2) 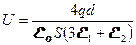 . Ответ: . Ответ: 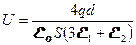 . . |
Задача 6. Металлический шар радиусом R=3см несет заряд Q=20 нКл. Шар окружен слоем парафина толщиной d=2 см. Определить энергию W электрического поля, заключенного в слое диэлектрика.
 Дано: R=3см=3·10-2 м Q=20 нКл= =20·10-9 Кл d=2 см=2·10-2м Дано: R=3см=3·10-2 м Q=20 нКл= =20·10-9 Кл d=2 см=2·10-2м  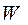 -? -? | Решение: Так поле, созданное заряженным шаром, является неоднородным, то энергия поля в слое диэлектрика распределена неравномерно. Однако Объемная плотность энергии будет одинакова во всех точках, отстоящих на равных расстояниях от центра сферы, так как поле заряженного шара обладает сферической симметрией. |
Выразим энергию в элементарном сферическом слое диэлектрика объемом dV 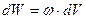 , (1) где ω – объемная плотность энергии. Полная энергия выразится интегралом , (1) где ω – объемная плотность энергии. Полная энергия выразится интегралом 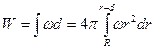 , (2) где r – радиус элементарного сферического слоя; dr – его толщина. Объемная плотность энергии определяется по формуле , (2) где r – радиус элементарного сферического слоя; dr – его толщина. Объемная плотность энергии определяется по формуле 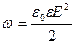 , где Е - напряженность поля, в нашем случае , где Е - напряженность поля, в нашем случае 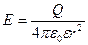 и, следовательно, и, следовательно, 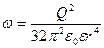 . (3) Подставив это выражение плотности в формулу (2) и вынеся за знак интеграла постоянные величины, получим . (3) Подставив это выражение плотности в формулу (2) и вынеся за знак интеграла постоянные величины, получим 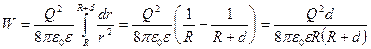 Подставляя значения в формулу найдем Подставляя значения в формулу найдем 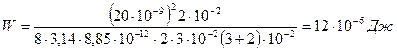 . Ответ: . Ответ: 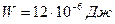 . . |
Задача 7. Амперметр сопротивлением 0,1 Ом имеет шкалу до 4 А. Какое сопротивление должно быть у шунта, чтобы увеличить предел измерения амперметра до 24 А?
Дано: R1 = 0,1 Ом; I1 = 4 A; I2 = 24 A.  Rш -? Rш -? |   Решение: Iш I2 I1 A Рис. 14 Решение: Iш I2 I1 A Рис. 14 |
Ток в неразветвленной части цепи I2 = I1 + Iш, но так как шунт и амперметр соединены параллельно, то U = IR1 = IшRш. 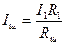 , т.е. I2 = I1 + , т.е. I2 = I1 + 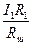 ; отсюда ; отсюда 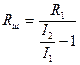 ; ; 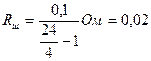 Ом. Ответ: Rш = 0,02 Ом. Ом. Ответ: Rш = 0,02 Ом. |
Задача 8. Вольтметр сопротивлением 200 Ом имеет шкалу до 60 В. Какое дополнительное сопротивление нужно подключить к вольтметру, чтобы увеличить предел измерения вольтметра до 300 В?
 |
Дано: R1 = 200 Ом; U1 = 60 В; U2 = 300 В.  R -? R -? | Решение:  R V Рис. 15 R V Рис. 15 |
При последовательном соединении напряжение на концах участка U2 = U1 + UR, так как ток во всех участках цепи одинаков, то 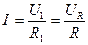 или или  , , 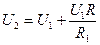 ; отсюда ; отсюда 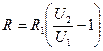 . . 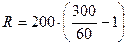 Ом = 800 Ом. Ответ: R = 800 Ом. Ом = 800 Ом. Ответ: R = 800 Ом. |
Задача 9. Как изменится температура медного провода, если по нему в течение 5 с проходит ток плотностью 9 А/мм2 и 25 % тепловой энергии отдается окружающим телам?
 Дано: t = 0,5 с; Дано: t = 0,5 с; 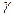 2 = 9 А/мм2 = 9.106 А/м; 2 = 9 А/мм2 = 9.106 А/м; 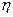 = 0,75 = 0,75  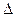 Т -? Т -? | Решение: Запишем выражение для КПД 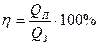 , (1) Qп – количество теплоты, затраченное на нагревание проводника. , (1) Qп – количество теплоты, затраченное на нагревание проводника. |
Qп = m c 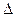 T, учитывая, что m = T, учитывая, что m = 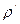 V, a V = l S, получим Qп = V, a V = l S, получим Qп = 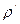 l S c l S c 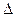 T, (2) T, (2) 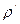 = 8900 кг/м3 – плотность меди; с = 380 Дж/(кг. К) – удельная теплоемкость меди; Qз – количество теплоты, которое выделится при прохождении электрического тока по проводнику. По закону Джоуля - Ленца Qз = I2Rt, учитывая, что I = jS, a R = = 8900 кг/м3 – плотность меди; с = 380 Дж/(кг. К) – удельная теплоемкость меди; Qз – количество теплоты, которое выделится при прохождении электрического тока по проводнику. По закону Джоуля - Ленца Qз = I2Rt, учитывая, что I = jS, a R =  , получим Qз = j2 , получим Qз = j2 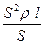 t = j2S t = j2S 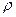 l t, (3) l t, (3) 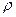 = 1,7.10-8 Ом . м – удельное сопротивление меди. Подставляем (2) и (3) в (1) = 1,7.10-8 Ом . м – удельное сопротивление меди. Подставляем (2) и (3) в (1) 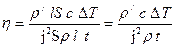 . . 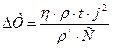 . . 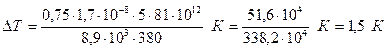 . Ответ: . Ответ:  Т = 1,5 К. Т = 1,5 К. |
Задача 10. Батарея элементов состоит из параллельно соединенных источников тока с ЭДС 5,5 В и внутренним сопротивлением каждого источника
5 Ом. При силе тока во внешней части цепи 2 А полезная мощность (т.е. мощность тока во внешней части цепи) равна 7 Вт. Сколько источников тока содержит батарея?
 Дано: Е = 5,5 В; r = 5 Ом; I = 2 А; Р = 7 Вт. n -? Дано: Е = 5,5 В; r = 5 Ом; I = 2 А; Р = 7 Вт. n -?  | Решение: Закон Ома для n параллельно соединенных источников тока с одинаковыми ЭДС и внутренними сопротивлениями: 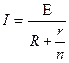 . (1) . (1) 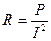 - внешнее сопротивление. (2) - внешнее сопротивление. (2) |
Подставляем (1) в (2) получим 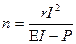 . . 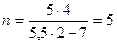 . Ответ: n = 5. . Ответ: n = 5. |
Задача 11. Сколько электроэнергии надо затратить для выделения в процессе электролиза 1 л кислорода при температуре 27 ОС и давлении 105 Па, если электролиз ведется при напряжении 10 В и КПД процесса 75 %?
Дано: V=1л = 10-3 м3; Т=27 ОС+ 273 ОС=300 К; U = 10 В; Р=105 Па; 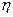 = 0,75; К=0,083.10-6 кг/Кл; = 0,75; К=0,083.10-6 кг/Кл; 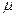 =32.10-3 кг/моль. =32.10-3 кг/моль.  А3 -? А3 -? |  Решение: Запишем формулу КПД Решение: Запишем формулу КПД 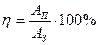 , (1) где АП = IUt – работа, совершаемая эл. током. (2) Силу тока выразим из закона Фарадея для электролиза m = Kit; , (1) где АП = IUt – работа, совершаемая эл. током. (2) Силу тока выразим из закона Фарадея для электролиза m = Kit; 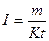 . (3) . (3) |
Подставим (3) в (2) 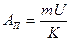 . (4) Массу кислорода найдем из уравнения Менделеева – Клапейрона . (4) Массу кислорода найдем из уравнения Менделеева – Клапейрона 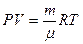 ; ; 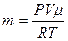 . (5) Подставим (5) в (4) . (5) Подставим (5) в (4) 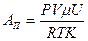 . (6) Подставим (6) в (1) получим . (6) Подставим (6) в (1) получим 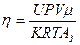 , отсюда , отсюда 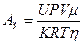 . . 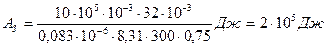 . Ответ: АЗ=2.105 Дж. . Ответ: АЗ=2.105 Дж. |
Задача 12. Термопара, сопротивление которой 6 Ом, позволяет определить минимальное изменение температуры 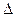 tмин = 0,006 0С. Найти сопротивление гальванометра, подключенного к термопаре. Постоянная термопары
tмин = 0,006 0С. Найти сопротивление гальванометра, подключенного к термопаре. Постоянная термопары 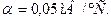
Дано: 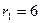 Ом; Ом; 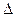 tмин = 0,006 0С; tмин = 0,006 0С; 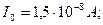  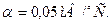 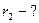 | 
Электродвижущая сила
С другой стороны, согласно закону Ома
| ||
где 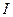 - сила тока в цепи термопары; - сила тока в цепи термопары; 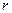 - полное сопротивление цепи; - полное сопротивление цепи; 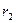 - сопротивление гальванометра. Приравнивая правые части (1) и (2), получим - сопротивление гальванометра. Приравнивая правые части (1) и (2), получим 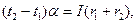 откуда откуда 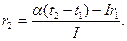 (3) Но (3) Но 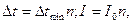 где где 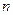 - число делений, на которое отклонилась стрелка гальванометра при силе тока - число делений, на которое отклонилась стрелка гальванометра при силе тока 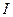 . Подставив указанные выражения . Подставив указанные выражения 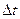 и и 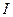 в (3) и сократив на в (3) и сократив на 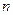 , получим , получим 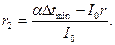 (4) Выпишем числовые значения в СИ и подставим их в (4): (4) Выпишем числовые значения в СИ и подставим их в (4): 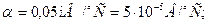 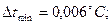 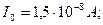 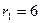 Ом; Ом; 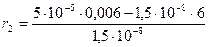 Ом = 14 Ом. Ответ: Ом = 14 Ом. Ответ: 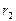 = 14 Ом. = 14 Ом. |
Задача 13. По двум длинным прямолинейным и параллельным проводам, расстояние между которыми 4 см, в противоположных направлениях текут токи 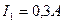 ,
, 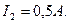 Найти магнитную индукцию поля в точке
Найти магнитную индукцию поля в точке 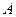 , которая находится на расстоянии 2 см от первого провода на продолжении линии, соединяющей провода.
, которая находится на расстоянии 2 см от первого провода на продолжении линии, соединяющей провода.
 Дано: Дано: 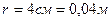 ; ; 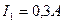 ; ; 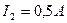 ; ; 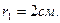  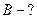 | Решение: 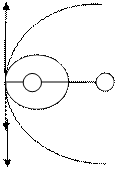
Рис. 16 | ||||||||||||
На рисунке провода расположены перпендикулярно к плоскости чертежа. Маленькими кружочками изображены сечения проводов. Условимся, что ток 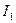 течет к нам, а ток течет к нам, а ток 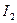 - от нас. Общая индукция - от нас. Общая индукция 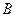 в точке в точке 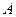 равна векторной (геометрической) сумме индукции равна векторной (геометрической) сумме индукции 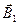 и и 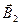 полей, создаваемых каждым током в отдельности, т.е. полей, создаваемых каждым током в отдельности, т.е. 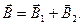 (1) Для того чтобы найти направление векторов (1) Для того чтобы найти направление векторов 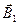 и и 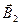 , проведем через точку , проведем через точку  силовые линии магнитных полей, созданных токами силовые линии магнитных полей, созданных токами 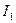 и и 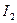 . Силовые линии магнитного поля прямого провода с током представляют собой концентрические окружности с центром на оси провода. Направление силовой линии совпадает с движением концов рукоятки правого буравчика, ввинчиваемого по направлению тока (правило буравчика). Поэтому силовая линия магнитного поля тока . Силовые линии магнитного поля прямого провода с током представляют собой концентрические окружности с центром на оси провода. Направление силовой линии совпадает с движением концов рукоятки правого буравчика, ввинчиваемого по направлению тока (правило буравчика). Поэтому силовая линия магнитного поля тока 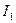 , проходящая через точку , проходящая через точку 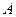 , представляет собой окружность радиусом , представляет собой окружность радиусом 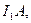 а силовая линия магнитного поля тока а силовая линия магнитного поля тока 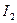 , проходящая через эту же точку, - окружность радиусом , проходящая через эту же точку, - окружность радиусом 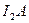 (на рис. 6 показана только часть этой окружности). По правилу буравчика находим, что силовая линия магнитного поля тока (на рис. 6 показана только часть этой окружности). По правилу буравчика находим, что силовая линия магнитного поля тока 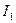 направлена против часовой стрелки, а тока направлена против часовой стрелки, а тока 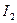 - по часовой стрелке. Теперь легко найти направление векторов - по часовой стрелке. Теперь легко найти направление векторов 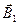 и и 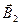 в точке в точке 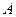 : каждый из них направлен по касательной к соответствующей силовой линии в этой точке. Так как векторы : каждый из них направлен по касательной к соответствующей силовой линии в этой точке. Так как векторы 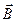 и и 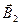 направлены вдоль одной прямой в противоположные стороны, то векторное равенство (1) можно заменить алгебраическим равенством направлены вдоль одной прямой в противоположные стороны, то векторное равенство (1) можно заменить алгебраическим равенством 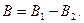 (2) Индукция магнитного поля тока (2) Индукция магнитного поля тока 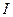 , текущего по прямому бесконечно длинному проводу, вычисляется по формуле , текущего по прямому бесконечно длинному проводу, вычисляется по формуле 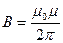 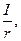 (3) где (3) где 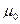 - магнитная постоянная; - магнитная постоянная; 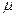 - магнитная проницаемость среды, в которой провод расположен; - магнитная проницаемость среды, в которой провод расположен; 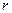 - расстояние от провода до точки, в которой определяется индукция. Подставив значения - расстояние от провода до точки, в которой определяется индукция. Подставив значения 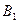 и и 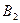 в равенство (2), получим в равенство (2), получим 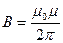 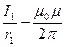 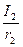 или или 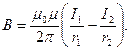 (4) Выразим числовые значения в СИ и подставим их в (4): (4) Выразим числовые значения в СИ и подставим их в (4): 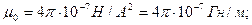 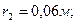 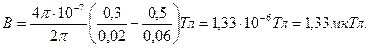 Ответ: Ответ: 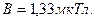 |
Задача 14. Электрон движется в однородном магнитном поле с индукцией 5 мТл по окружности. Найти период его обращения. Масса электрона 9,1.10-31 кг, модуль его заряда 1,6.10-19 Кл.
 Дано: В = 5 мТл = 5.10-3 Тл; m = 9,1.10-31 кг; е = 1,6.10-19 Кл. Дано: В = 5 мТл = 5.10-3 Тл; m = 9,1.10-31 кг; е = 1,6.10-19 Кл.  Т -? Т -? | Решение: На заряд, движущийся в магнитном поле, действует сила Лоренца 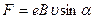 , (1) где , (1) где 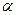 = 900 и sin 90 = 1. По второму закону Ньютона эта сила F = m = 900 и sin 90 = 1. По второму закону Ньютона эта сила F = m 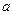 , , |
где 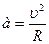 - центростремительное ускорение, тогда - центростремительное ускорение, тогда 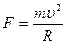 . (2) Приравниваем правые части (1) и (2) . (2) Приравниваем правые части (1) и (2) 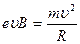 . Учитывая, что . Учитывая, что 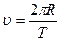 . . 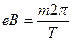 , отсюда , отсюда 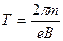 . . 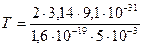 с = 7.10-9 с. Ответ: Т = 7 нс. с = 7.10-9 с. Ответ: Т = 7 нс. |
Задача 15. В однородное магнитное поле индукцией 10-4 Тл влетает 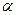 -частица со скоростью 2.103 м/с под углом 300 к направлению вектора индукции. Определить радиус витков траектории
-частица со скоростью 2.103 м/с под углом 300 к направлению вектора индукции. Определить радиус витков траектории 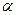 -частицы и расстояние, пройденное ею вдоль силовых линий поля за три витка.
-частицы и расстояние, пройденное ею вдоль силовых линий поля за три витка.
 |
Дано: В = 10-4 Тл; 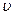 = 600 м/с; = 600 м/с; 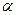 = 300; т = 6,7.10-27 кг; q = 3,2.10-19 К. = 300; т = 6,7.10-27 кг; q = 3,2.10-19 К.  R -? S -? R -? S -? | Решение: 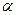 - частица в магнитном поле будет перемещаться по винтовой линии. - частица в магнитном поле будет перемещаться по винтовой линии.  у S у S
Рис. 17 | ||||||||
Из формулы силы Лоренца 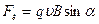 (1) видно, что ее величина зависит от значения составляющей скорости, направленной перпендикулярно вектору В: (1) видно, что ее величина зависит от значения составляющей скорости, направленной перпендикулярно вектору В: 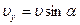 . (2) Вторая составляющая скорости, направленная вдоль силовой линии, определяет скорость перемещения . (2) Вторая составляющая скорости, направленная вдоль силовой линии, определяет скорость перемещения  - частицы вдоль поля: - частицы вдоль поля: 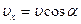 . (3) . (3) | |||||||||
Радиус витков траектории  - частицы найдем, решая систему уравнений: - частицы найдем, решая систему уравнений:
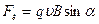
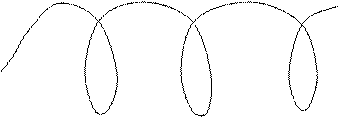
Величина нормального ускорения а будет определяться составляющей скорости
Величину перемещения
Период вращения
Подставляя в формулу (5) выражения (6), (2) и (3) получаем значение перемещения
Ответ: R = 0,21 м, S = 6,8 м. |
Задача 16. В однородном магнитном поле находится плоский виток радиусом 0,05 м, расположенный перпендикулярно к линиям поля. Какой ток потечет по витку, если индукция магнитного поля за время 0,2 с равномерно изменяется от 0,1 Тл до 0,2 Тл? Сопротивление витка 0,5 Ом.
Дано: r = 0,05 м; 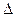 t = 0,2 c; B1 = 0,1 Тл; B2 = 0,2 Тл; R = 0,5 Ом. t = 0,2 c; B1 = 0,1 Тл; B2 = 0,2 Тл; R = 0,5 Ом.   I -? I -? | Решение: Искомая сила тока 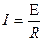 , где С – э.д.с. индукции, , где С – э.д.с. индукции, 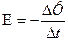 . Приращение магнитного потока равно . Приращение магнитного потока равно 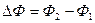 . Площадь контура . Площадь контура 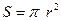 . . |
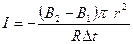 . . 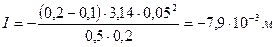 . Знак минус означает, что магнитное поле индукционного тока противоположно внешнему магнитному полю. Ответ: I = -7,9.10-3 м. . Знак минус означает, что магнитное поле индукционного тока противоположно внешнему магнитному полю. Ответ: I = -7,9.10-3 м. |
Задача 17. На немагнитный каркас длиной 50 см и площадью сечения 3 см2 намотан в один слой провод диаметром 0,4 мм так, что витки плотно прилегают друг к другу. Найти индуктивность получившегося соленоида и магнитный поток, пронизывающий поперечное сечение соленоида при токе 1 А.
Дано: l = 50 см; S = 3 см2; d = 0,4 мм; I = 1 A.   L -? Фм -? L -? Фм -? | Решение: Индуктивность соленоида вычисляется по формуле 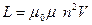 , (1) где n – число витков, приходящихся на единицу длины соленоида; V – объем соленоида. Число витков n получим, разделив единицу длины на диаметр провода d: , (1) где n – число витков, приходящихся на единицу длины соленоида; V – объем соленоида. Число витков n получим, разделив единицу длины на диаметр провода d: |
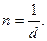 (2) Объем соленоида V = S l, где S – площадь поперечного сечения соленоида, l – длина соленоида. Подставим выражения для n и V в равенство (1): (2) Объем соленоида V = S l, где S – площадь поперечного сечения соленоида, l – длина соленоида. Подставим выражения для n и V в равенство (1): 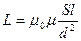 , где , где 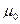 = 4 = 4 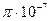 Гн/м, Гн/м, 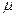 = 1. = 1. 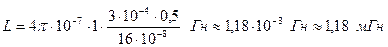 . При наличии тока в соленоиде любое его поперечное сечение пронизывает магнитный поток Фм = BS, (3) где В – магнитная индукция в соленоиде. Магнитная индукция соленоида определяется по формуле: . При наличии тока в соленоиде любое его поперечное сечение пронизывает магнитный поток Фм = BS, (3) где В – магнитная индукция в соленоиде. Магнитная индукция соленоида определяется по формуле: 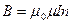 . (4) Подставив выражения (2) и (4) в (3), получим расчетную формулу . (4) Подставив выражения (2) и (4) в (3), получим расчетную формулу 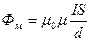 . . 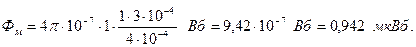 Ответ: L Ответ: L 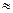 1,18 мГн, Фм = 0,942 мкВб. 1,18 мГн, Фм = 0,942 мкВб. |
Задача 18. Ток, текущий в рамке, содержащей 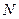 витков, создает магнитное поле. В центре рамки индукции поля
витков, создает магнитное поле. В центре рамки индукции поля 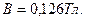 Найти магнитный момент рамки, если ее радиус
Найти магнитный момент рамки, если ее радиус 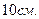
 Дано: Дано: 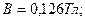  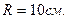 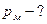 | Решение: Магнитный момент рамки с током 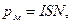 (1) где (1) где 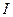 - сила тока в витке; - сила тока в витке; |
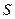 - площадь, охватываемая витком - площадь, охватываемая витком 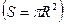 ; ; 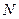 - число витков в рамке. Индукция магнитного поля в центре кругового тока (многовиткового) - число витков в рамке. Индукция магнитного поля в центре кругового тока (многовиткового) 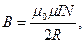 откуда откуда 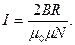 Подставляя в (1) выражения для Подставляя в (1) выражения для 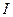 и и 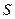 , получим , получим 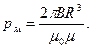 (2) Выпишем числовые значения величин в СИ и подставим их в расчетную формулу (2): (2) Выпишем числовые значения величин в СИ и подставим их в расчетную формулу (2): 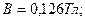 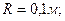 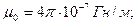 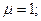 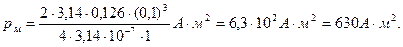 Ответ: Ответ: 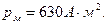 |
Задача 19. Плоская рамка площадью 100 см2, содержащая 20 витков тонкого провода, вращается в однородном магнитном поле с индукцией 100 мТл. Амплитуда э. д. с. индукции 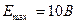 . Определить частоту вращения рамки.
. Определить частоту вращения рамки.
 |
Дано: 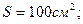 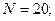 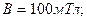  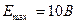 . . 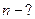 | Решение: Для определения частоты вращения рамки используем понятие угловой скорости вращения: 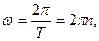 где где 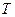 - период вращения; - период вращения; 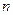 - частота вращения. Отсюда - частота вращения. Отсюда 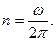 (1) (1) |
Угловую скорость вращения найдем из соотношения 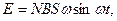 (2) где (2) где 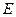 - мгновенное значение э. д. с. индукции. Амплитудой - мгновенное значение э. д. с. индукции. Амплитудой 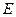 является значение является значение 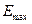 , соответствующее значению , соответствующее значению 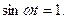 Из соотношения (2) имеем Из соотношения (2) имеем 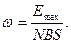 (3) Подставив выражение (3) Подставив выражение 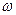 по (3) в (1), получаем по (3) в (1), получаем 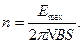 Выразим значения всех величин, входящих в формулу, в СИ: Выразим значения всех величин, входящих в формулу, в СИ: 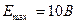 ; ; 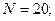 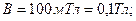 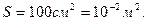 Выполним вычисления: Выполним вычисления: 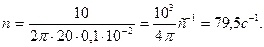 Ответ: Ответ:  |
 2015-02-27
2015-02-27 7259
7259








 r1 E2
r1 E2
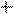



 F -?
F -? 
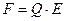 , (1)
, (1)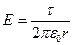 , (2) где τ – линейная плотность заряда. Выразим линейную плотность τ через поверхностную плотность σ. Для этого выделим элемент цилиндра длиной l и выразим находящейся на нем заряд Q1 двумя способами:
, (2) где τ – линейная плотность заряда. Выразим линейную плотность τ через поверхностную плотность σ. Для этого выделим элемент цилиндра длиной l и выразим находящейся на нем заряд Q1 двумя способами: 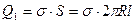 и
и 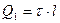 . (3) Приравняв правые части этих неравенств, получим
. (3) Приравняв правые части этих неравенств, получим 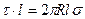 . После сокращения на l найдем
. После сокращения на l найдем 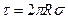 . С учетом этого формула (2) примет вид
. С учетом этого формула (2) примет вид 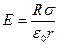 . Подставив это выражение в формулу (1), найдем искомую силу:
. Подставив это выражение в формулу (1), найдем искомую силу: 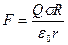 . (4) Подставим значения и найдем искомую силу
. (4) Подставим значения и найдем искомую силу 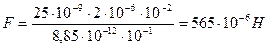 . Ответ:
. Ответ: 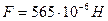 Задача 5.Воздушный конденсатор с зарядом на обкладках q1 площадью обкладок S и расстоянием между ними d погружают в жидкость с диэлектрической проницаемостью E2 на
Задача 5.Воздушный конденсатор с зарядом на обкладках q1 площадью обкладок S и расстоянием между ними d погружают в жидкость с диэлектрической проницаемостью E2 на 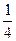 его объема. Найти напряжение на обкладках конденсатора после погружения.
его объема. Найти напряжение на обкладках конденсатора после погружения.  U -?
U -? 

 Решение: с1
Решение: с1 










 E1 с2
E1 с2 
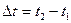 ее спаев, вычисляется по формуле
ее спаев, вычисляется по формуле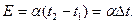 (1)
(1)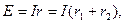 (2)
(2)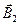
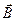


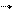






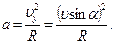
 получим,
получим,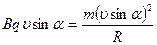 , отсюда
, отсюда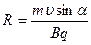 . (4)
. (4)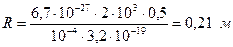 .
.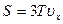 . (5)
. (5)
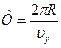 . (6)
. (6)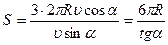 ;
; 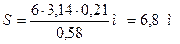 .
.