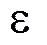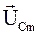Вынужденные колебания в электрической цепи

Колебания, возникающие в электрической цепи, содержащей R, L,C (рис.2), под действием внешней переменной электродвижущей силы 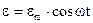, называются вынужденными.

Рис. 2

Вынужденные колебания в электрической цепи описываются уравнением 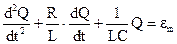(5)

(5)

где 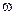– циклическая частота переменной ЭДС, С^-1.

Переменная ЭДС возбуждает в цепи переменный ток той же частоты 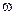, изменяющейся по закону

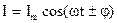(6)

где 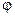– сдвиг по фазе между током и ЭДС

В общем случае ток и ЭДС в такой цепи по фазе не совпадают. Значения тока и сдвиг по фазе зависят от параметров цепи R, L, C.

Рассмотрим электрическую цепь (рис. 2), где R, L, C соединены последовательно с ЭДС. Выясним, как изменяется напряжения на каждом из участков R, L, C.

По закону Ома напряжение на участке R выразится формулой:

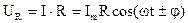(7)

Из сравнения (6) и (7) видим, что напряжение на активном сопротивлении R и ток совпадает по фазе. На векторной диаграмме амплитудные значения этих величин откладываем вдоль одной прямой, рис.3.

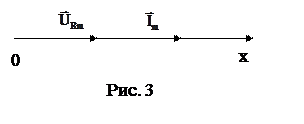Из формулы (7) ясно, что амплитудное значение напряжения 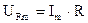, где R – активное сопротивление, определяющее необратимые затраты энергии на ленц – джоулево тепло (потребляет мощность).

Напряжение на катушке индуктивности L определяется по формуле

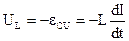
где 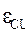– ЭДС самоиндукции В.

После дифференцирования (6) и замены функции синуса на косинус получим формулу 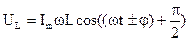(8)

(8)

Сравнивая (6) и (8) видим, что напряжение U_L опережает ток по фазе на 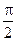. На векторной диаграмме это выглядит так: (рис. 4)

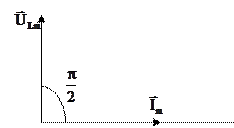Из формулы (8) запишем

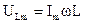(9)

где U_Lm – амплитудное значение напряжения;

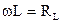– индуктивное сопротивление, которое определяет затраты энергии на возбуждение магнитного поля в катушке.

Напряжение на конденсаторе определяется по формуле

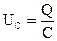
Учитывая (6) и то, что 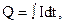после интегрирования и перехода к функции косинуса получим формулу

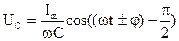(10)

где 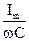– амплитудное значение напряжения на конденсаторе (U_Cm);

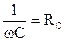– ёмкостное сопротивление, определяющее потери энергии на возбуждение электрического поля в конденсаторе.

Из (6) и (10) видно, что напряжение U_C отстаёт от тока по фазе на 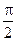. Векторная диаграмма для этого случая изображена на рис. 5.

Рис. 5

Сопротивления 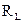и 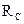называются реактивными, т.е. при их наличии энергия не расходуется на нагревание проводников.

В замкнутой цепи, изображенной на рис. 2, для каждого момента времени имеет место соотношение

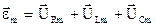(11)

Посмотрим (рис.6) векторную диаграмму сложения напряжений в цепи, учитывая сдвиг фаз между ними и током. Для этого выберем ось Х и под углом (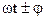) к ней проводим прямую, на которой откладываем I_m и U_Rm.От этой прямой вверх под углом 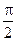откладываем U_Lm, а вниз под углом 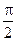откладываем U_Cm и производим сложение векторов U_Lm и U_Cm и U_Rm.В результате сложения получим вектор .

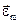Проекции векторов 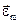, I_m, U_Lm, U_Cm и U_Rm на ось Х представляют собой мгновенные значения этих величин. Взаимное расположение векторов, изображенное на рис.6, сохраняется для любого момента времени. Но в зависимости от соотношения между абсолютными значениями векторов U_Lm и U_Cm ток может отставать от ЭДС по фазе

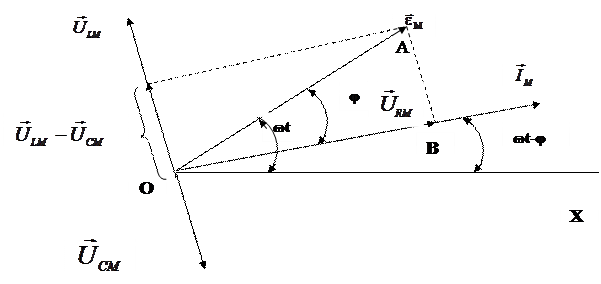
Рис.6

(как на рис. 6), а может и опережать, если 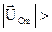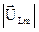. Из 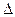ОАБ следует

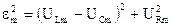
После преобразования с учетом амплитудных значений величин U_Lm, U_Cm и U_Rm получим формулу

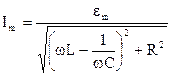(12)

Формула (12) является законом Ома для цепи переменного тока. Величина 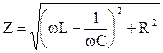является сопротивлением цепи переменного тока, содержащей R, L, C соединенные последовательно. Из 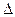ОАБ (рис. 6) находим сдвиг по фазе между током и ЭДС по формуле

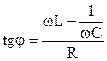(13)