Ситуация, в которой оказалась Агафья Тихоновна, свойственна процессу принятия практически всех управленческих решений. Для обоснованного выбора варианта решения используется экономико-математическое моделирование, построенное на аналитических выражениях. Началом этой области математики явились исследования, выполненные в 1938–39 гг. советским математиком, лауреатом Нобелевской премии Л.В. Канторовичем. Экономико-математическая модель – это математическое описание исследуемого экономического процесса. Эта модель выражает закономерности экономического процесса в абстрактном виде с помощью математических соотношений.
Как правило, выделяют три этапа экономико-математического моделирования:
– постановка цели и задачи исследований, на базе чего производиться качественное описание объекта (процесса) в виде экономической модели;
– формирование математической модели и оценка адекватности ее реальному экономическому процессу;
– выбор или разработка метода решения модели, подготовка исходных данных, выполнение расчётов, анализ полученных результатов с точки зрения пригодности для практического использования.
Процедура экономико-математического моделирования используется в тех случаях, когда имеется множество допускаемых решений и заменяет дорогостоящие и трудоемкие натурные эксперименты расчётами.
В настоящее время разработаны различные методы оптимального управления разнообразными процессами в экономке, военном деле, на транспорте, в технике, построенные на основе математического программирования с использованием теории и численных методов решения многомерных экстремальных задач с ограничениями на область допустимых значений. Сюда относятся методы линейного, нелинейного, динамического и параметрического программирования.
Основоположником использования экономико-математи-ческого моделирования на речном транспорте является В.И. Савин, которым совместно с Д.И. Валовым в 1959 г. была разработана методика оптимизации распределения грузового флота по участкам работы (грузопотокам). С тех пор различными авторами было предложено множество моделей использования транспортного флота, которые в силу разнообразных причин (в основном в силу ограниченных ресурсов вычислительной техники) не были доведены до практического использования. Однако часть постановок была реализована.
Так в 1973 г. С.М. Пьяных была разработана экономико-математическая модель оптимизации закрепления транспортного флота за грузопотоками, реализованная при обосновании графика движения флота применительно к системе смежных пароходств Центрального и Северо-Западного бассейнов.
Функция цели (критерий эффективности) – минимум эксплуатационных расходов на содержание транспортного флота
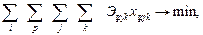 | (10) |
i = 1,2,3, …, m; p = 1,2,3, …, φ; j = 1,2,3 ,…,n; k = 1,2,3, …, ψ.
Функция цели должна выполняться при следующих ограничениях.
1. Требование выполнения планового грузооборота на грузопотоке прямого направления
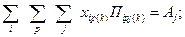 | (11) |
2. Требование выполнения планового грузооборота на грузопотоке обратного направления
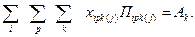 | (12) |
3. Запрет использования судов на некоторых вариантах освоения грузопотоков
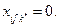 | (13) |
4. Перевозки должны быть выполнены имеющимися ресурсами флота:
4.1. Грузового самоходного
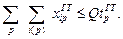 | (14) |
4.2. Грузового несамоходного
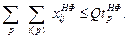 | (15) |
4.3. Тяговых средств
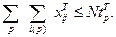 | (16) |
5. Неотрицательность переменных
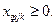 | (17) |
В модели (10)–(17) приняты обозначения:
| i | – | индекс типа судна (состава); |
| j | – | индекс грузопотока прямого направления; |
| k | – | индекс грузопотока обратного направления; |
| j*, k* | – | индексы грузопотоков, которые не могут осваиваться i- м типом судов; |
| p | – | индекс пароходства – владельца флота; |
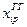 , , 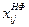 , , 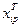 | – | обыскиваемое количество тоннажа (тяги) i -го типа p-го пароходства, необходимое для освоения j- го (k -го) грузопотока, тнж(с) – сут.; |
| П ipj(k); П ipk(j) | – | провозная способность i -го типа судна (состава) при освоении j - го (k -го) грузопотока, ткм; |
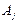 , Аk , Аk | – | плановый размер грузооборота на j- ом (k -ом) грузопотоках, ткм; |
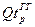 , , 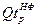 , , 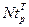 | – | плановые (балансовые) ресурсы грузового самоходного, несамоходного и буксирного флота p-го пароходства, тнж(с) – сут; |
| Э ipjk | – | расходы по содержанию транспортного флота i -го типа p-го пароходства при освоение j -го и k -го грузопотоков, руб/тнж(с) – сут. |
Индексы j(k) означают признак освоения j -ого грузопотока в сочетании с k -м, а k(j) – освоение k -го грузопотока в сочетании с j -м.
Решение модели (10)–(17) позволяет получить оптимальный план использования флота с определением потребности во флоте в тнж (с) – сут. на освоение каждого грузопотока.
Модель легко адаптируется к любым условиям работы флота. Это может быть схема освоения перевозок грузов в системе смежных пароходов (при наличии арендных отношений) или в каком-либо отдельном пароходстве. Результатами решения могут быть определение потребности во флоте в единицах судов (составов) или размера судопотока оптимального типа судна (состава) на сочетании грузопотоков j и k.
В качестве критерия эффективности можно использовать разнообразные эксплуатационно-экономические показатели: минимум себестоимости перевозок; максимум провозной способности флота, прибыли, производительности труда плавсостава и т.д.
В 1978 г. в составе автоматизированной подсистемы «График» пароходства Волготанкер была реализована экономико-математическая модель, разработанная В.В. Золотовым.
Функция цели, минимизирующая расходы по содержанию транспортного флота, имеет вид
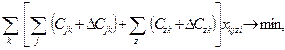 , , | (18) |
| i =1,2,3,…, m; j =1,2,3,…, n; k =1,2,3,…, φ; z =1,2,3,…,ψ. |
Ограничения модели:
1. Требование освоения плановых объемов перевозок
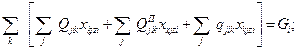 | (19) |
2. Перевозки должны быть выполнены имеющимися ресурсами грузового флота
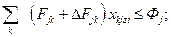 | (20) |
3. Перевозки должны быть выполнены имеющимися ресурсами буксирного флота
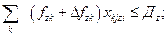 | (21) |
4. Отыскиваемый план не должен быть отрицательным
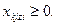 | (22) |
В модели (18)–(22) приняты обозначения:
| i | – | индекс грузопотока; |
| j | – | индекс типа тоннажа; |
| z | – | индекс типа тяги; |
| k | – | индекс кругового рейса; |
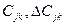 , , 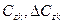 | – | соответственно расходы по содержанию тоннажа j -го типа и тяги z -го типа на основном грузопотоке и по досылке отпауженного груза (индекс Δ) за один круговой рейс, руб/судо-сут; |
 | – | отыскиваемый план – размер судопотока на k -oм круговом рейсе; |
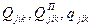 | – | соответственно загрузка j -ого тоннажа на i -ом грузопотоке до и после паузки, а также количество отпауженного груза из одного теплохода (состава) на k -oм грузовом рейсе, т; |
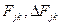 , , 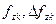 | – | потребность j -го типа тоннажа и z -ого типа тяги на основном грузопотоке и по досылке отпауженного груза (индекс Δ) на k -oм круговом рейсе за одно отправление, ед; |
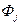 , , 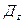 | – | ресурсы тоннажа j -ого типа и тяги z -ого типа, ед; |
 | – | размер i -го грузопотока, т. |
Автором модели (18)–(22) кроме того, был разработан алгоритм автоматизированного формирования базовой схемы освоения грузопотоков (варианты всевозможного сочетания грузопотоков прямого и обратного направлений и освоения их разными типами судов (состав). Следует отметить, что рассматриваемая модель носит универсальный характер, поскольку адаптирована к переменным глубинам внутренних водных путей.
В практике экономических обоснований используется математическое моделирование оптимального распределения однородных грузов (наливных, хлебных, руд, углей и т.п.) между различными видами транспорта. Функционал – минимизация издержек на доставку грузов
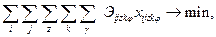 | (23) |
| i = 1,2,3 ,…,m; j = 1,2,3 ,…,n; z = 1,2,3,…, τ; k = 1,2,3,…, ψ; j = 1,2,3,…, σ. |
1. Потребность каждого j -ого пункта в z -м продукте удовлетворяется в полном объеме
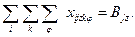 | (24) |
2. Из каждого i -ого пункта z -й продукт должен быть полностью вывезен
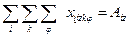 . . | (25) |
3. Количество используемого подвижного состава φ –го типа на k -м виде транспорта не может превышать наличного парка.
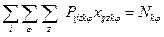 . . | (26) |
4. Отыскиваемый план не должен быть отрицательным
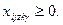 | (27) |
В моделях (23)–(27) приняты обозначения:
| i, j | – | признаки пункта отправления и назначения; |
| z | – | признак рода груза; |
| k, j | – | признаки вида транспорта и типа подвижного состава; |
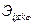 | – | расходы на перемещение единицы z -го рода груза из i -го пункта в j -й пункт назначения с использованием j- го подвижного соcтава k -го вида транспорта включая расходы по погрузке, транспортировке, выгрузке, хранению и перевалке, руб; |
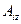 , , 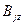 | – | объемы производства и потребления z -го рода груза в i -м и j -м пунктах, т; |
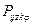 | – | удельная потребность подвижного состава j -го типа k -го вида транспорта на перемещение единицы z -го рода груза между i -м и j -м пунктами, т; |
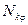 | – | наличие подвижного состава j -го типа на k -м виде транспорта, т.тнж; |
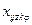 | – | отыскиваемый план, определяющий объем перевозок z -го рода груза из i -го в j -й пункт с использованием j -го типа подвижного состава на k -м виде транспорта, т; |
Модель (23)–(27) предусматривает решение закрытой задачи (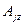 =
= 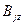 ), при наличии открытой задачи (
), при наличии открытой задачи (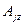 ≠
≠ 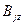 ), вводят или фиктивного поставщика (в случае
), вводят или фиктивного поставщика (в случае 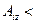
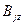 ), или фиктивного потребителя (в случае
), или фиктивного потребителя (в случае 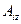 >
> 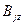 ).
).
Методы линейного программирования нашли широкое применение при оптимизации работы портов.
Для обоснования оптимального сменно-суточного плана работы грузового причала используется экономико-математическая модель (28)–(33), минимизирующая расходы по содержанию флота и причала за время обработки судна
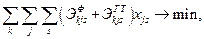 | (28) |
| j = 1, 2, 3 ,…,m; k = 1, 2, 3 ,…,n; s = 1, 2, 3,…, φ. |
1. Объем переработки грузов должен быть выполнен или перевыполнен
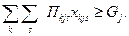 | (29) |
2. Продолжительность работы каждой перегрузочной машины не должна превышать имеющихся ресурсов времени
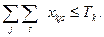 | (30) |
3. Ресурсы рабочей силы механизаторов не должны быть превышены
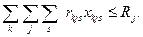 | (31) |
4. Время пребывания судна под обработкой не должно превышать планового
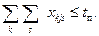 | (32) |
5. Неотрицательность отыскиваемого плана
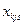 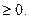 | (33) |
При построении модели (28)–(33) используются обозначения:
| k | – | индекс перегрузочной машины; |
| j | – | индекс причала; |
| s | – | индекс варианта концентрации перегрузочных машин на j -м причале; |
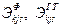 | – | расходы по судну и причалу, относимые на час работы k -го типа машин на j -м причале при s -м варианте концентрации машин, руб; |
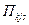 | – | производительность одной машины k -го типа на j -ом причале при s -м варианте концентрации машин, т/ч; |
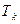 | – | ресурсы рабочего времени k -й перегрузочной машины, ч; |
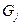 | – | плановый объем переработки грузов на j -м причале за смену, т; |
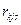 | – | потребность рабочей силы для обслуживания одной машины k -го типа на j -ом причале при s -м варианте концентрации машин, чел-ч; |
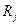 | – | ресурсы рабочей силы на планируемую смену, выделенные для работы на j -й причал, чел-ч; |
| t п | – | плановое время грузовой обработки судна, ч; |
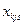 | – | отыскиваемый план – количество часов работы k -го типа машины на j -м причале при s -м варианте концентрации, ч; |
Оптимальная расстановка перегрузочных машин (например, плавучей механизации различных типов) по участкам работы реализуется на базе экономико-математической модели (34)–(37), обеспечивающей максимальную суммарную сменную производительность
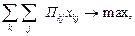 | (34) |
| k = 1, 2, 3, …, m; j =1, 2, 3, …,n. |
При ограничениях:
1. Объем переработки грузов на каждом j -м причале должен быть не менее заданного
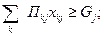 | (35) |
2. Общие затраты машино-смен перегрузочных машин не должны превышать имеющиеся ресурсы
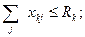 | (36) |
- Неотрицательность отыскиваемого плана
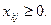 | (37) |
В модели (34)–(37) приняты обозначения:
| k | – | индекс типа перегрузочной машины; |
| j | – | индекс причала; |
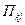 | – | сменная производительность работы k -й машины на j -м причале, т; |
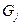 | – | плановый сменный объем переработки грузов на j -м причале, т; |
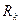 | – | ресурсы k -го типа перегрузочных машин, машино-смен; |
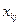 | – | отыскиваемый план – потребность k -го типа машин на j -ом участке, машино-смен. |
В практической деятельности эксплуатационного аппарата зачастую возникает необходимость распределения судов по причалам грузовой обработки, обладающим разной механовооруженностью. Оптимальное решение подобной задачи обеспечивает экономико-математическая модель (38)–(41), минимизирующая суммарные затраты времени на обработку заданного количества судов
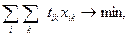 | (38) |
| i = 1, 2, 3, …,m; k = 1, 2, 3, …,n, |
при ограничениях:
1. Все суда должны быть обработаны
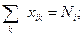 | (39) |
2. Общая занятость причала не должна превышать ресурсы рабочего времени
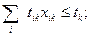 | (40) |
3. Неотрицательность плана
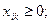 | (41) |
Приняты обозначения:
| k | – | индекс причала; |
| i | – | индекс типа судна; |
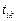 | – | затраты времени на обработку i -го типа судна на k -ом причале, ч; |
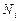 | – | плановое количество судов i -го типа, подлежащего обработке на k -ом причале, ед; |
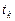 | – | ресурс рабочего времени k -го причала за период планирования, ч; |
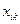 | – | отыскивается план – количество судов i -го типа подлежащих обработке на k -ом причале, ед. |
Модели (28)–(41) в разное время апробировались в практике эксплуатационных обоснований оптимизации работы различных портов и отдельных причалов (порт Ахтубинск, Камский грузовой район, причал Сормовской нефтебазы и ряд других).
Следует отметить, что современный этап развития экономики в целом характеризуется некоторой неопределенностью. Это неопределенность оказывает влияние на спрос услуг транспорта, что обусловило необходимость разработки специальных моделей (параметрическое программирование) и методов обоснования оптимальных вариантов использования транспортных средств.
При распределении ресурсов флота и портов исходные данные задаются не жестко (детерминировано), а с учётом допустимых отклонений, характеризующихся коэффициентом λ (0 ≤ λ ≤ 1). При λ = 0 осваивается только гарантированная часть объема перевозок, при λ = 1 – полный объем. Постановкой задачи требуется произвести расстановку имеющихся ресурсов судов таким образом, чтобы обеспечить полное освоение гарантированной части объема перевозок и определенной доли переменного объема при минимальных издержках по флоту
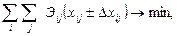 | (42) |
| i = 1, 2, 3, …, m; j = 1, 2, 3, …,n. |
Ограничениями модели параметрического программирования являются нижеприведенные.
1. Требование освоения гарантированного и части переменного объема перевозок
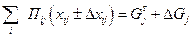 . . | (43) |
2. Ограничение по использованию ресурсов судов
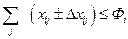 . . | (44) |
3. Отыскиваемые переменные должны быть положительными величинами, а суммарная потребность в судах для освоения переменного объема перевозок должна ровняться нулю
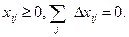 | (45) |
4. Коэффициент, учитывающий колебания переменной части объема перевозок, должен находиться в пределах
| 0 ≤ λ ≤ 1. | (46) |
В модели (42)–(46) приняты обозначения:
| j | – | индекс грузопотока; |
| i | – | индекс типа судна; |
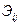 | – | эксплуатационные расходы по одному судну i -го типа при освоении j -го грузопотока, руб; |
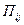 | – | провозная способность одной единицы i -го типа при работе на j -м грузопотоке, т; |
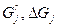 | – | гарантированный и переменный размеры j -го грузопотока, т; |
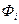 | – | ресурсы судов i -го типа, ед; |
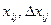 | – | отыскиваемый план соответственно потребность в судах i -го типа для освоения гарантированного и переменного объема перевозок на j -м грузопотоке, ед. |
В связи с недостаточными объемами финансирования в последние годы наблюдается уменьшение гарантированных габаритов судового хода, следствием чего является падение провозной способности флота. При разработке программы развития речного транспорта Ханты-Мансийского автономного округа была впервые использована комплексная экономико-математическая модель обоснования мероприятий по выполнению перевозок грузов и путевых работ, предусматривающая оптимизацию расстановки судов по грузопотокам и выполнение в оптимальных размерах дноуглубительных работ на основе минимума совокупных затрат
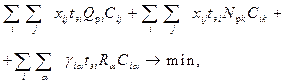 | (47) |
| i = 1, 2, 3, …, m; j = 1, 2, 3, …,n; α = 1, 2, 3,…, φ; k = 1, 2, 3,…,ψ. |
При условиях:
1. Перевозки на каждом j -м грузопотоке должны быть выполнены
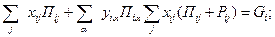 | (48) |
2. Имеющиеся ресурсы самоходного или несамоходного тоннажа не должны быть превышены
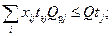 | (49) |
3. Имеющиеся ресурсы тяги не должны быть превышены
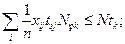 | (50) |
4. Имеющиеся ресурсы дноуглубительных караванов не должны быть превышены
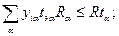 | (51) |
5. Углубление судового хода должно выполняться не более необходимых пределов
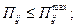 | (52) |
6. Отыскиваемые переменные должны быть положительными величинами
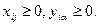 | (53) |
В модели приняты обозначения:
| i | – | признак грузопотока; |
| j | – | признак типа самоходного или несамоходного тоннажа; |
| k | – | признак типа тяги; |
| α | – | признак типа дноуглубительного каравана (под караваном понимается совокупность земснаряда, брандвахты, мотозавозней, шаланд и тяги для отвода грунта за пределы судового хода или рефулера); |
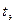 | – | период эксплуатации соответствующего технического средства, сут; |
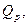 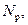 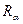 | – | регистровые грузоподъемность теплохода (баржи), мощность тяги и суточная паспортная производительность земснаряда, т, л.с., тыс. куб. м; |
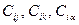 | – | стоимость содержания тоннажа, тяги и куб. м выполнения дноуглубительных работ, руб/тнж (сило) – сут, руб/куб. м; |
 | – | размер i -го грузопотока, т; |
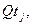 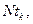 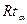 | – | ресурсы тоннажа, тяги и дноуглубительного каравана, тнж-сут, сило-сут, тыс. куб. м-сут; |
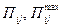 | – | провозная способность одного теплохода (состава) при бытовых габаритах судового хода и максимальная, соответствующая максимальной осадке, обеспечивающей выполнение заданного объема перевозок грузов (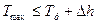 ), т; ), т; |
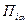 | – | эксплуатационная производительность одного каравана α -го типа при выполнении путевых работ на трассе i -го грузопотока за период выполнения работ на этом грузопотоке, тыс. куб.м; |
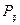 | – | прирост проводной способности одного теплохода (состава) при увеличении на одну единицу габаритов судового хода, т; |
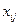 | – | отыскиваемый план, определяющий необходимое число теплоходов (составов) j -го типа на освоении i -го грузопотока, ед; |
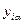 | – | отыскиваемый план, определяющий необходимое число караванов α-го типа для создания приемлемых габаритов судового хода на трассе i -го грузопотока, ед; |
Приведенные выше модели (10)–(53) предназначены для решения задач линейного программирования, являются базовыми и их можно адаптировать к различным условиям путем введения дополнительных ограничений. Методы решения линейных задач сегодня довольно хорошо изучены и излагаются в специальной литературе. Математический аппарат для реализации того или иного метода может быть построен на базе ППП MathLab.
Говорят, что цифры правят миром.
Нет, они только показывают,
как править миром.
Иоганн Волофганг Гёте
 2015-02-14
2015-02-14 717
717








