2.1. Краткие теоретические сведения
2.1.1. Основные понятия и определения
Электрический ток, меняющийся во времени, называют переменным током. Если изменения напряжений и токов в цепях происходят по гармоническому закону, то такие цепи называются цепями гармонического (синусоидального) тока. Вид кривой синусоидального тока показан на рис.2.1.
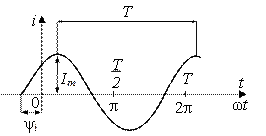
Рис.2.1.Кривая синусоидального тока
Ток записывается в виде синусоидальной функции:
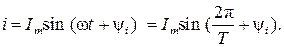
Максимальное значение функции Im называют амплитудой тока; T − период изменения тока; ψ i − начальная фаза тока. Частота тока − число колебаний за одну секунду: f= 1/ T, 1/с (Гц). Величину ω =2π/ T называют угловой частотой и измеряют в рад./с. Аргумент синусоидальной функции (ω t + ψ i) называют фазой. Текущее значение i называют мгновенным значением тока.
То же самое можно сказать и о синусоидальном напряжении:
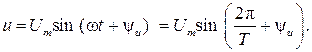
Очевидно, что в цепях гармонического тока частота тока и напряжения одинаковы, а вот начальные фазы могут отличаться. Рассмотрим рис. 2.2, где изображены кривые тока и напряжения.

Рис.2.2. Кривые синусоидального тока и напряжения
В зависимости от того, в какой точке принято начало отсчета времени (начало координат на рис. 2.2), будут изменяться и начальные фазы тока и напряжения. Но разность фаз останется неизменной и равной φ. Поэтому при рассмотрении процессов в цепях гармонического тока начало координат при изображении кривых тока и напряжения совмещают с точкой перехода через ноль либо кривой напряжения, либо тока. Тогда начальная фаза одной из функций будет равна нулю, а другой φ. Так, если совместить на рис. 2.2 начало координат с точкой перехода через ноль тока, то выражения для тока и напряжения примут вид:
i=Im sin ω t; u=Um sin (ω t + φ).
Если совместить начало координат с точкой перехода через ноль напряжения, то выражения для тока и напряжения примут вид:
i=Im sin (ω t − φ); u=Um sin ω t.
Для характеристики гармонического тока применяется понятие действующего значения (его называют также эффективным или среднеквадратичным). Под действующим значением тока I понимается постоянный ток, который оказывает такое же тепловое действие при прохождении через активное сопротивление, что и переменный ток:
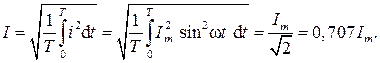
Аналогично определяют и действующее значение гармонического напряжения: 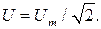
Отметим, что именно действующее значение измеряют приборы электромагнитной и электродинамической систем, которые используются при снятии показаний в лабораторных работах.
Рассмотрим, как ведут себя в цепях гармонического тока пассивные двухполюсники − элементы электрической цепи: активное сопротивление R, индуктивность L и емкость C.
При протекании тока по активному сопротивлению возникает падение напряжения, которое связано с мгновенным значением тока законом Ома:
u=Ri. (2.1)
Отсюда следует, что начальные фазы тока и напряжения совпадают, т.е. сдвиг фаз между током и напряжением равен нулю.
Индуктивность в цепи гармонического тока ведет себя иначе. При протекании тока по индуктивности возникает магнитное поле. Если ток переменный, то и магнитное поле (а следовательно, и магнитный поток) также изменяется во времени. На основании закона электромагнитной индукции переменный магнитный поток вызывает появление в индуктивности ЭДС самоиндукции, направленной против причины, вызвавшей ее появление. Математически данное утверждение выражается соотношением: 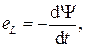 где Ψ − потокосцепление, связанное с током iL, протекающим по индуктивности, формулой Ψ= LiL. Величина L носит название индуктивности и имеет размерность Гн (Генри). Для линейных цепей L= const, поэтому выражение для ЭДС самоиндукции примет вид
где Ψ − потокосцепление, связанное с током iL, протекающим по индуктивности, формулой Ψ= LiL. Величина L носит название индуктивности и имеет размерность Гн (Генри). Для линейных цепей L= const, поэтому выражение для ЭДС самоиндукции примет вид
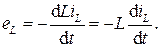
Этой ЭДС соответствует падение напряжения uL, направленное в противоположную сторону, поэтому
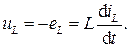 (2.2)
(2.2)
Для гармонического тока iL =Im sin ω t, тогда
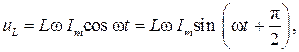
откуда следует, что разность фаз между напряжением и током составляет π/2, т.е. напряжение в индуктивности опережает по фазе ток на 90º. Величина L ω обозначается XL, имеет размерность Ом и называется реактивным сопротивлением индуктивности.
Емкость представляет собой элемент электрической цепи, способный накапливать электрический заряд Q. При этом соотношение между величиной заряда и напряжением uC на емкости имеет вид
Q=CuC.
Величина C носит название емкости и имеет размерность Ф (Фарад). Для линейных цепей C= const.
Если напряжение, приложенное к емкости, изменяется, то изменяется и накопленный в ней заряд. Как известно, изменение заряда означает протекание электрического тока. Тогда величину тока, протекающего через емкость, найдем из выражения
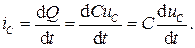 (2.3)
(2.3)
Для гармонического напряжения uС =Um sin ω t, тогдаполучим
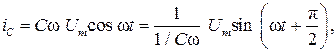
откуда следует, что разность фаз между напряжением и током составляет π/2, т.е. ток в емкости опережает по фазе напряжение на 90º. Величина 1/ C ω обозначается XС, имеет размерность Ом и называется реактивным сопротивлением емкости.
2.1.2. Основы символического метода
В цепях гармонического тока напряжения и ток в реактивных элементах связаны через операции дифференцирования и интегрирования. Поэтому расчеты установившихся режимов во временной области должны вестись путем решения дифференциальных уравнений, что в случае расчета сложных цепей приводит к трудно разрешимым проблемам. Переход в комплексную область позволяет свести расчеты цепей гармонического тока к решению алгебраических уравнений с использованием методов расчета цепей постоянного тока. Рассмотрим основы символического метода, который основан на символическом изображении действительных синусоидальных функций времени комплексными числами (этот метод иногда называют методом комплексных амплитуд).
Из курса математики известна формула Эйлера
e j α = cos α + j sin α.
Угол α в этой формуле может принимать любые значения. Положим α=ω t+ ψ, тогда на основании формулы Эйлера запишем
e j (ω t +t )= cos (ω t+ ψ) + j sin (ω t+ ψ).
Согласно теории комплексных чисел последнее выражение представляет собой комплексное число, модуль которого равен единице, а аргумент является функцией времени. Умножим данное уравнение на Im, тогда получим
Im e j (ω t + ψ)= Im cos (ω t+ ψ) + j Im sin (ω t+ ψ).
Полученное выражение представляет собой комплексное число с модулем Im и аргументом (ω t+ ψ). На комплексной плоскости оно изображается в виде вектора длиной Im, вращающегося против часовой стрелки с угловой частотой ω (рис.2.3). Тогда проекции вектора на оси координат представляют собой гармонические функции.
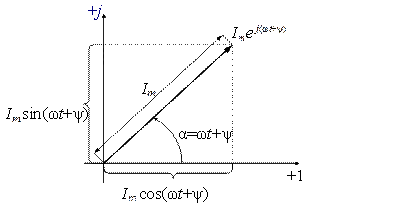
Рис.2.3. Изображение числа Im e j (ω t + ψ)на комплексной плоскости
Как видно из рисунка, синусоидальный ток Im sin(ω t+ ψ) может рассматриваться как проекция вектора Im e j (ω t + ψ)на мнимую ось. Данное обстоятельство позволяет сделать вывод о взаимно-однозначном соответствии между гармонической функцией и комплексным числом, т.е.
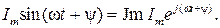
Отметим, что в радиотехнической литературе данное взаимно-однозначное соответствие устанавливается между косинусоидальной функцией и соответствующим комплексным числом, т.е.
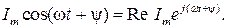
Если на комплексной плоскости изобразить другой вектор, например,
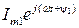 , то он будет также вращаться с угловой частотой ω против часовой стрелки, но угол между этими векторами будет неизменным и равным разности начальных фаз ψ и ψ1.
, то он будет также вращаться с угловой частотой ω против часовой стрелки, но угол между этими векторами будет неизменным и равным разности начальных фаз ψ и ψ1.
Представим число Im e j (ω t + ψ)в виде произведения Imej ψ e j ω t . Комплексное число Imej ψ будет представлять собой вектор длиной Im с аргументом ψ, неподвижный относительно координатной плоскости. Сомножитель e j ω t носит название оператора вращения, поскольку умножение комплексного числа на него приводит к вращению вектора с частотой ω. Комплексное число Imej ψ называют комплексной амплитудой.
То же самое можно сказать и для числа 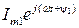 . Тогда векторы, изображающие комплексные амплитуды Imej ψ и
. Тогда векторы, изображающие комплексные амплитуды Imej ψ и 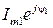 , на комплексной плоскости будут неподвижны, а угол между ними будет равен разности начальных фаз ψ и ψ1.
, на комплексной плоскости будут неподвижны, а угол между ними будет равен разности начальных фаз ψ и ψ1.
В цепях гармонического тока все напряжения и токи имеют одинаковую частоту, равную частоте источника, поэтому в уравнениях, описывающих процессы в электрических цепях в комплексном виде, сомножитель e j ω t будет общим для всех членов соответствующих уравнений. Очевидно, его можно сократить. Тогда формальное взаимно-однозначное соответствие устанавливают между гармоническими функциями и их комплексными амплитудами. Комплексная амплитуда обозначается точкой вверху индекса: 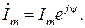
Математические действия над гармоническими функциями во временной области имеют свои соответствия в комплексной области. Не приводя строгих математических доказательств, дадим связь основных математических действий над гармоническими функциями во временной области с соответствующими им действиями в комплексной области над комплексными амплитудами.
Если x=Xm sin(ω t+ ψ x) и y=Ym sin(ω t+ ψ y), то им соответствуют комплексные амплитуды 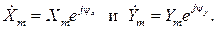 Соответствующие действия над ними отражены в табл. 2.1.
Соответствующие действия над ними отражены в табл. 2.1.
Соответствие действий во временной и комплексной областях Таблица 2.1
| Действие во временной области | Действие в комплексной области |
| kx, k - постоянное число | 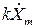 |
| x±y | 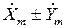 |
| xy | 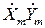 |
| x/y | 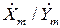 |
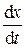 | 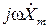 |
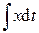 | 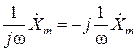 |
Действия над комплексными амплитудами производятся в соответствии с правилами действий над комплексными числами. Таким образом, дифференцирование и интегрирование во временной области в комплексной области заменяются алгебраическими операциями умножения и деления на комплексное число j ω.
2.1.3. Комплексное представление элементов электрической цепи
Связь между током и напряжением в элементах электрической цепи определяется соотношениями (2.1)...(2.3). В соответствии с табл. 2.1 можно установить связь между ними на основании правил действий над комплексными амплитудами. Соответствующие формулы сведены в табл. 2.2.
Описание элементов электрической цепи Таблица 2.2
| Элемент цепи | Временная область | Комплексная область |
| R | u=Ri | 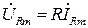 |
| L | 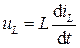 или или 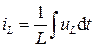 | 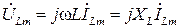 или или 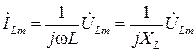 |
| C | 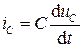 или или 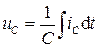 | 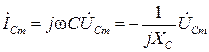 или или 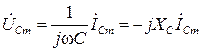 |
При переходе в комплексную область элементы электрической цепи заменяются на соответствующие комплексные сопротивления:
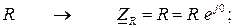
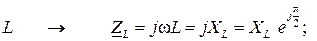 (2.4)
(2.4)
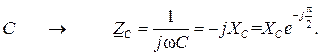
Тогда соотношения между комплексными амплитудами напряжений и токов на соответствующих элементах принимают формальный вид закона Ома в комплексной области:
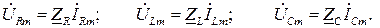 (2.5)
(2.5)
Рассмотрим, каковы фазовые соотношения между током и напряжением на каждом из двухполюсников.
Пусть ток, протекающий по каждому из двухполюсников, имеет вид
i=Im sin ω t, тогда комплексная амплитуда тока: 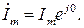 В соответствии с выражениями (2.4) и (2.5) запишем
В соответствии с выражениями (2.4) и (2.5) запишем
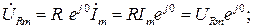
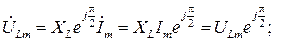 (2.6)
(2.6)
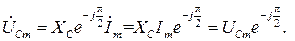
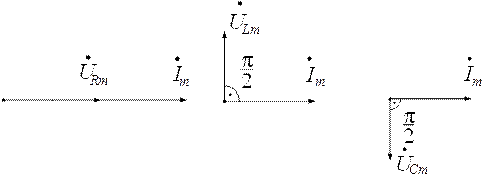
Векторы тока и напряжений двухполюсников на комплексной плоскости представлены на рис.2.4.
а) б) в)
Рис. 2.4. Векторные диаграммы токов и напряжений двухполюсников:
а) для активного сопротивления; б) для индуктивности;
с) для емкости
Диаграммы показывают наглядно фазовые соотношения между напряжениями и токами в пассивных двухполюсниках: в активном сопротивлении ток и напряжение совпадают по фазе, в индуктивности ток отстает от напряжения на 90º, а в емкости ток опережает приложенное напряжение на 90º.
Заметим, что при описании двухполюсников можно вместо амплитудных значений токов и напряжений использовать их действующие значения. Все формулы сохраняют свой вид, только вместо амплитудных значений токов и напряжений в них подставляют действующие значения. При проведении лабораторного практикума измеряемые приборами значения токов и напряжений являются действующими значениями, поэтому при использовании формул (2.4)...(2.6) и табл. 2.2 следует использовать действующие значения.
2.1.4. Расчет цепей гармонического тока
Как указывалось выше, с использованием символического метода можно существенно упростить расчет цепей гармонического тока. Для иллюстрации сказанного рассмотрим методику расчета цепи с последовательным и параллельным соединением R, L, C и входным гармоническим напряжением u=Um sin ω t.
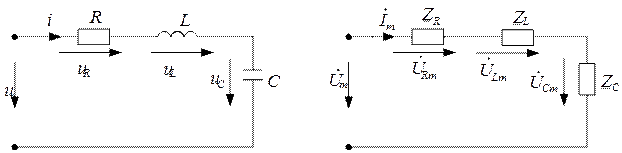
1. Последовательное соединение R, L, C (рис. 2,5,а).
а) б)
Рис. 2.5. Расчетная схема: а) во временной области;
б) в комплексной области
Вначале осуществляют переход в комплексную область, изображая исходную схему с заменой всех величин их комплексными изображениями (рис. 2.5,б). Положительные направления тока и напряжений при этом на элементах цепи сохраняют во всех ветвях схемы.
По своему виду схема рис. 2.5,б напоминает резистивную цепь постоянного тока. Ее расчет можно вести любым известным методом расчета цепей постоянного тока, только с использованием комплексных изображений элементов и комплексных амплитуд напряжений и токов.
Для данной схемы с последовательным соединением элементов вначале найдем входное сопротивление 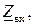 которое равно сумме комплексных сопротивлений цепи
которое равно сумме комплексных сопротивлений цепи
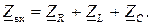
Тогда комплекс тока найдем из очевидного соотношения
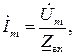
где 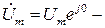 комплексная амплитуда входного напряжения.
комплексная амплитуда входного напряжения.
С учетом (2.4) получим
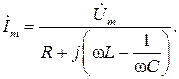
Для получения комплекса тока 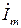 произведем деление, переведя комплексное число в знаменателе в показательную форму,
произведем деление, переведя комплексное число в знаменателе в показательную форму,
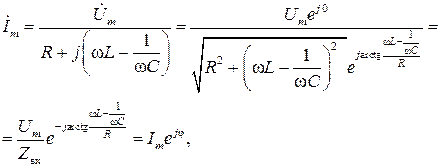
где 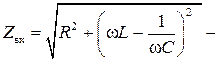 модуль комплексного входного сопротивления;
модуль комплексного входного сопротивления; 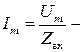 - амплитуда тока в цепи,
- амплитуда тока в цепи, 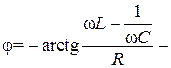 фаза тока.
фаза тока.
Комплекс входного сопротивления
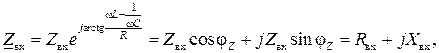 (2.7)
(2.7)
где 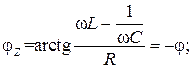
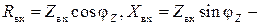 соответственно активная и реактивная составляющие входного сопротивления.
соответственно активная и реактивная составляющие входного сопротивления.
Падение напряжения на каждом двухполюснике найдем с использованием (2.6)
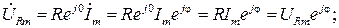
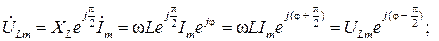
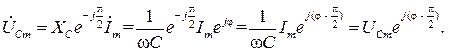
Переходя во временную область, найдем ток и падения напряжения на каждом элементе цепи при нулевой фазе входного напряжения 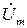 :
:
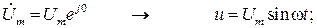
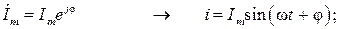

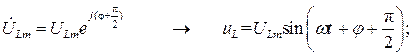
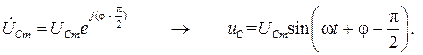
Таким образом, цепь гармонического тока рассчитана без применения операций дифференцирования, а лишь с использованием алгебраических действий в комплексной области.
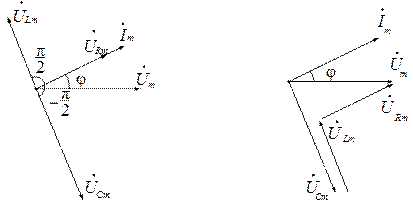
Изображая на комплексной плоскости вектора, соответствующие комплексам тока и напряжений, наглядно можно оценить фазовые сдвиги (рис. 2.6).
а) б)
Рис. 2.6. Векторная диаграмма для последовательной цепи:
а) фазовые соотношения между векторами;
б) сложение векторов напряжений в контуре цепи
Поскольку задача решалась в общем виде, для определенности примем, что напряжение 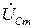 (соответственно и реактивное сопротивление XС) на емкости больше напряжения
(соответственно и реактивное сопротивление XС) на емкости больше напряжения 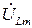 (и реактивного сопротивления XL) на индуктивности. Поэтому цепь по отношению к источнику носит активно-емкостной характер, и ток по фазе опережает напряжение источника на угол φ.
(и реактивного сопротивления XL) на индуктивности. Поэтому цепь по отношению к источнику носит активно-емкостной характер, и ток по фазе опережает напряжение источника на угол φ.
На векторной диаграмме (рис. 2.6,б) произведено сложение векторов напряжений двухполюсников в соответствии с ЗНК. При этом учитываются принятые в исходной схеме (рис. 2.5) положительные направления тока и напряжений на элементах цепи. Согласно ЗНК алгебраическая сумма падений напряжения в контуре равна нулю:
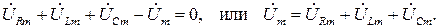
Таким образом, в комплексной форме законы Кирхгофа выполняются при условии учета фазовых сдвигов между напряжениями, которые должны складываться в векторной форме. Уместно отметить, что во временной области законы Кирхгофа выполняются для мгновенных значений:
uR+uL+uC−u= 0, или u= uR+uL+uC.
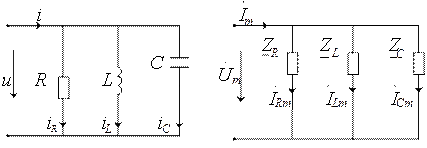
2. Параллельное соединение R,L,C (рис. 2.7,а)
а) б)
Рис.2.7. Расчетная схема: а) во временной области;
б) в комплексной области
Переход в комплексную область осуществляется заменой всех величин их комплексными изображениями (рис. 2.7,б).
Ток в каждом двухполюснике определится по закону Ома:
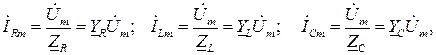 (2.8)
(2.8)
где 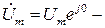 комплексная амплитуда входного напряжения;
комплексная амплитуда входного напряжения;
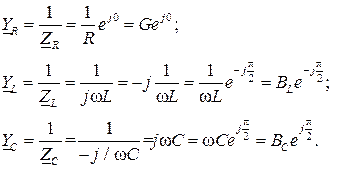
Здесь обозначено: 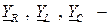 комплексные проводимости сопротивления, индуктивности и емкости соответственно;
комплексные проводимости сопротивления, индуктивности и емкости соответственно; 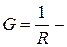 активная проводимость;
активная проводимость; 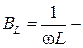 реактивная проводимость индуктивности;
реактивная проводимость индуктивности; 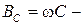 реактивная проводимость емкости.
реактивная проводимость емкости.
Ток 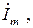 потребляемый цепью, на основании ЗТК будет равен сумме токов двухполюсников:
потребляемый цепью, на основании ЗТК будет равен сумме токов двухполюсников: 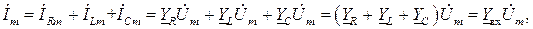
откуда следует, что комплексная входная проводимость цепи 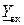 равна сумме комплексных проводимостей параллельно соединенных элементов.
равна сумме комплексных проводимостей параллельно соединенных элементов.
Подставляя в последнее выражение значения комплексных проводимостей, запишем
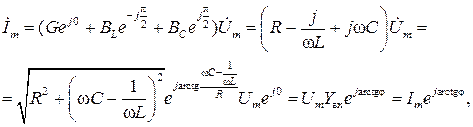
где 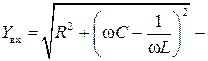 модуль комплексной входной проводимости;
модуль комплексной входной проводимости; 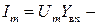 амплитуда входного тока;
амплитуда входного тока; 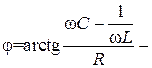 фаза тока.
фаза тока.
В соответствии с (2.8) запишем выражения для токов в ветвях:
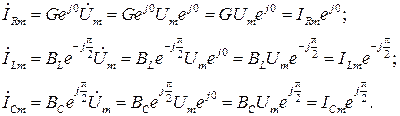
Переходя во временную область, найдем токи в ветвях цепи при нулевой фазе входного напряжения 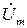 :
:
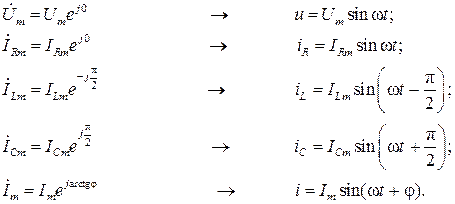
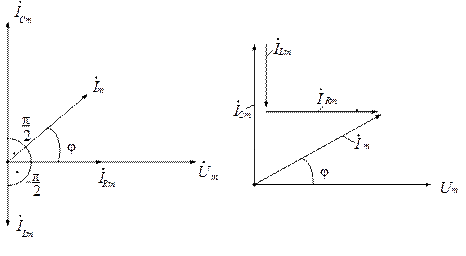
Изображая на комплексной плоскости вектора, соответствующие комплексам входного напряжения и токов в ветвях цепи, наглядно можно оценить фазовые сдвиги (рис. 2.8).
Поскольку задача решалась в общем виде, то здесь принято, что ток в емкости 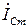 (соответственно и реактивная проводимость BC), больше тока
(соответственно и реактивная проводимость BC), больше тока 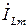 (и реактивной проводимости BL) в индуктивности. Поэтому цепь по отношению к источнику носит активно-емкостной характер, и ток по фазе опережает напряжение источника на угол φ.
(и реактивной проводимости BL) в индуктивности. Поэтому цепь по отношению к источнику носит активно-емкостной характер, и ток по фазе опережает напряжение источника на угол φ.
а) б)
Рис. 2.8. Векторная диаграмма для параллельной цепи:
а) фазовые соотношения между векторами;
б) сложение векторов токов в ветвях цепи
На векторной диаграмме (рис. 2.8,б) произведено сложение векторов токов двухполюсников в соответствии с ЗТК. При этом учитываются принятые в исходной схеме (рис. 2.7) положительные направления токов в ветвях. Согласно ЗТК алгебраическая сумма токов в узле равна нулю:
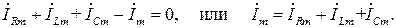
Таким образом, в комплексной форме ЗТК выполняется при условии учета фазовых сдвигов между токами, которые должны складываться в векторной форме. Уместно отметить, что во временной области ЗТК выполняется для мгновенных значений:
iR+iL+iC−i= 0, или i= iR+iL+iC.
2.1.5. Мощность в цепи гармонического тока
Мгновенное значение мощности p в цепи переменного токаопределяется формулой
p=ui,
где u,i − мгновенные значения напряжения и тока соответственно.
Среднее значение мощности P за период T переменного тока определяется выражением
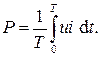
Для синусоидальных напряжения и тока u=Um sin ω t и i=Im sin (ω t + φ), тогда можно записать
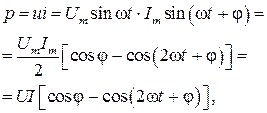 (2.9)
(2.9)
где U,I − действующие значения напряжения и тока.
Среднее значение мощности в цепи гармонического тока
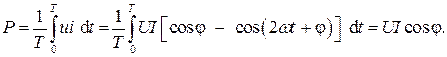 (2.10)
(2.10)
Данная мощность определяет энергию, подводимую к цепи за определенный промежуток времени, называется активной мощностью и измеряется в ваттах (Вт). Множитель cosφ называют коэффициентом мощности.
Прибор, осуществляющий измерение мощности в цепях переменного тока, называется ваттметром. Он измеряет активную мощность в соответствии с выражением (2.10).
Перепишем выражение (2.9) в ином виде:
p = UI cos φ − UI (cos φ cos 2ω t − sin φ sin 2ω t) =
= UI cos φ(1− cos 2ω t) + UI sin φ sin 2ω t = p а + p р. (2.11)
Первое слагаемое в (2.11) представляет собой мгновенную активную мощность p а, изменяющуюся с двойной частотой от нуля до удвоенного среднего значения. Это мощность, выделяющаяся в активном сопротивлении в виде теплоты.
Мощность p р является мгновенной реактивной мощностью, изменяющейся с двойной частотой с амплитудой UI sin φ. Среднее значение мгновенной реактивной мощности p р, очевидно, равно нулю.
Реактивная мощность характеризует непрерывный обмен энергией между источником и цепью, содержащей реактивные элементы, где энергия источника преобразуется в энергию магнитного поля индуктивности и электрического поля емкости и затем возвращается обратно в источник. Амплитуда UI sinφ мгновенной реактивной мощности p р обозначается Q, называется реактивной мощностью и измеряется в вольт-амперах (ВАР).
Амплитуда мгновенной мощности UI в (2.9) и (2.11) носит название полной или кажущейся мощности, обозначается латинской буквой S и измеряется в вольт-амперах (ВА).
Полная мощность через активную и реактивную мощности выражается соотношением 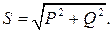
Графически эту связь можно представить в виде прямоугольного треугольника - треугольника мощности, один катет которого численно равен P, другой катет равен Q, а гипотенуза S.
В символической форме комплекс полной мощности 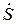 определяется через комплекс напряжения и сопряженный комплекс тока. Так, если напряжение на некотором участке цепи обозначить
определяется через комплекс напряжения и сопряженный комплекс тока. Так, если напряжение на некотором участке цепи обозначить 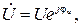 а ток
а ток 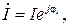 то, умножая комплекс напряжения
то, умножая комплекс напряжения 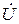 на сопряженный комплекс тока
на сопряженный комплекс тока 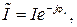 получим
получим
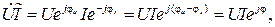
где φ= (φ u − φ i) − угол сдвига фаз между напряжением и током.
Тогда
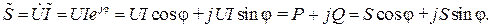
Связь между полной S и активной P мощностью дает простой способ опытного определения коэффициента мощности:
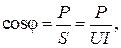 (2.12)
(2.12)
где U,I − измеренные приборамидействующие значения напряжения и тока, P − активная мощность в цепи, измеренная ваттметром.
На щитке любого источника электрической энергии переменного тока (генератора, трансформатора и т.д.) указывается величина S. Она характеризует ту мощность, которую этот источник может отдавать потребителю, если потребитель будет работать при cosφ=1, т.е. будет представлять чисто активное сопротивление.
Измеренные значения тока I, напряжения U и активной мощности P в цепи позволяют определить параметры самой цепи − полное, активное и реактивное сопротивление (соответственно Z, R, X). Действительно, величина полного сопротивления равна:
Z=U/I;
а в соответствии с (2.6) активное сопротивление 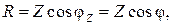 а реактивное сопротивление
а реактивное сопротивление 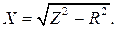
2.1.6. Резонанс в цепи гармонического тока
В общем случае двухполюсник в цепи гармонического тока содержит индуктивности, емкости и активные сопротивления. По отношению ко внешней цепи такой двухполюсник ведет себя как активно-индуктивная цепь, или активно-емкостная, в зависимости от того, какое из реактивных сопротивлений преобладает. Под резонансным режимом работы двухполюсника понимают режим, при котором его входное сопротивление является чисто активным, не смотря на наличие реактивных элементов. Отсюда следует, что условием возникновения режима резонанса является равенство нулю мнимой части входного сопротивления. В этом случае напряжение и ток на входе двухполюсника совпадают по фазе (cosφ=1), а реактивная мощность двухполюсника равна нулю (sinφ=0).
При рассмотрении резонанса будем оперировать с комплексами действующих значений напряжений и токов.
Различают резонанс напряжений и резонанс токов.
Резонанс напряжений имеет место в цепи с последовательным соединением R, L, C (рис. 2.9,а).
Комплекс входного сопротивления последовательной цепи
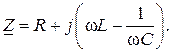
Условием резонанса является равенство нулю мнимой части 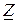 , т.е.
, т.е.
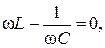
откуда определяем резонансную частоту ω0
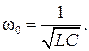 (2.13)
(2.13)
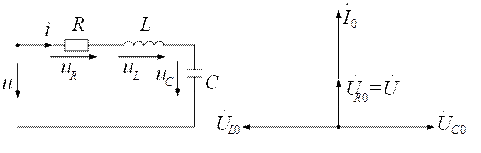
а) б)
Рис. 2.9. Схема с последовательным соединением элементов:
а) схема цепи; б) векторная диаграмма
при резонансе напряжений
Таким образом, режим резонанса можно достичь либо изменением частоты напряжения источника ω, либо изменением величины индуктивности L, либо изменением величины емкости С.
При резонансе входное сопротивление цепи 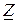 минимально и равно активному сопротивлению R, а ток достигает максимальной величины. Напряжения на реактивных элементах при резонансе
минимально и равно активному сопротивлению R, а ток достигает максимальной величины. Напряжения на реактивных элементах при резонансе 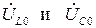 одинаковы по величине и противоположны по фазе, поэтому на векторной диаграмме, изображающей напряжения на элементах (рис. 2.7,б), они компенсируют друг друга, а входное напряжение
одинаковы по величине и противоположны по фазе, поэтому на векторной диаграмме, изображающей напряжения на элементах (рис. 2.7,б), они компенсируют друг друга, а входное напряжение 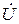 равно падению напряжения на активном сопротивлении:
равно падению напряжения на активном сопротивлении: 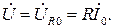 При этом напряжения на индуктивности и емкости могут быть достаточно велики и превосходить входное напряжение.
При этом напряжения на индуктивности и емкости могут быть достаточно велики и превосходить входное напряжение.
Сопротивления реактивных элементов при резонансной частоте называют волновым сопротивлением ρ
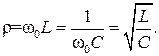
Отношение напряжения на реактивном сопротивлении при резонансе к приложенному напряжению называется добротностью Q
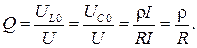
Обратное отношение называется затуханием цепи d
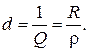
Добротность показывает, во сколько раз напряжение на индуктивности или на емкости превышает напряжение на входе схемы при резонансе. В радиотехнических устройствах Q может доходить до 300 и больше.
Поскольку при резонансе цепь ведет себя как чисто активная, энергия, поступающая от источника, покрывает только потери энергии в активном сопротивлении. При этом происходит обмен запасенной энергией между емкостью и индуктивностью без возврата ее в источник.
Входное сопротивление последовательного контура является функцией частоты. Зависимости действительной и мнимой части входного сопротивления от частоты называют частотными характеристиками контура. Они позволяют определить поведение резонансного контура в окрестности резонансной частоты и оценить влияние добротности на его свойства. С частотными характеристиками можно ознакомиться в любом учебнике по ТОЭ или учебном пособии. В настоящем лабораторном практикуме для исследования резонанса используют источник с фиксированной частотой, а резонанс достигается изменением величины емкости. Поэтому рассмотрим, как изменяются входное сопротивление, напряжения на элементах и ток в цепи при изменении величины емкости.
Входное сопротивление двухполюсника
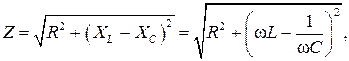 (2.14)
(2.14)
а действующее значение тока в цепи
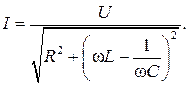
Здесь переменной величиной является емкость C.
Рассмотрим зависимости составляющих сопротивления Z в функции C (рис. 2.10). Активное сопротивление R и реактивное сопротивление индуктивности XL с изменением емкости не меняются, поэтому их графики представляют собой прямые, параллельные оси абсцисс.
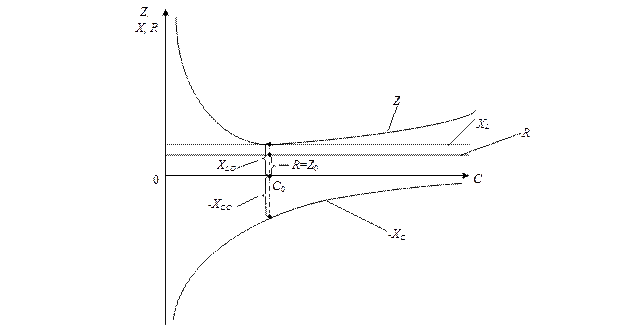
Рис. 2.10. Графики изменения сопротивлений контура
Реактивное сопротивление XC =1/ω C в функции емкости изменяется в обратной пропорции. Суммируя ординаты кривых сопротивлений в соответствии с (2.14), получим график изменения входного сопротивления Z в функции емкости. При величине емкости C 0, соответствующей резонансной частоте, входное сопротивление достигает минимального значения Z 0= R. Очевидно, что кривая тока I будет иметь выраженный максимум в этой же точке (рис. 2.11).
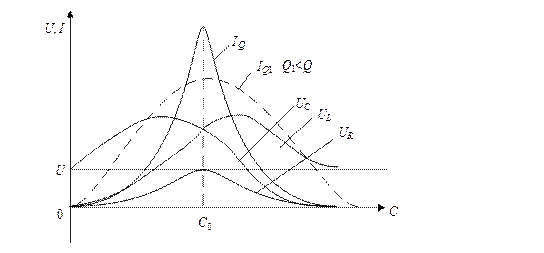
Рис.2.11. Резонансные кривые последовательного контура
Напряжение на активном сопротивлении UR будет иметь максимум при резонансе.
Напряжение на емкости UC будет изменяться от величины напряжения источника U при ω=0, как на рис. 2.11, через максимум до нуля при ω→∞.
Напряжение на индуктивности UL будет меняться от нуля при ω=0 через максимум при резонансе до величины напряжения источника при ω→∞.
Форма кривой тока будет зависеть от добротности, т.е. от величины активного сопротивления. При меньшей добротности (Q 1˂ Q) кривая тока IQ 1 (на рис. 2.11 изображена пунктиром) идет более полого, а ток при резонансной частоте меньше, чем при высокой добротности. Таким образом, чем больше добротность контура, тем более острой (пикообразной) становится форма кривой тока.
Резонанс токов имеет место в цепи с параллельным соединением R, L, C (рис. 2.12,а).
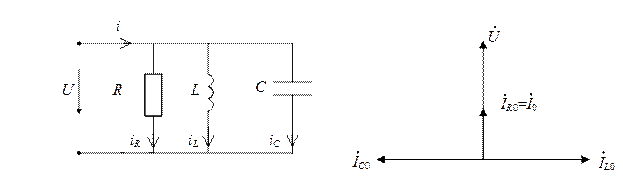
а) б)
Рис. 2.12. Схема с параллельным соединением элементов:
а) схема цепи; б) векторная диаграмма при резонансе токов
Комплекс входной проводимости 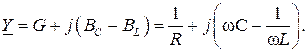
Условием резонанса является равенство нулю мнимой части 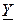 , т.е.
, т.е.
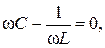
откуда определяем резонансную частоту ω0
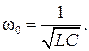
Таким образом, режим резонанса можно достичь либо изменением частоты напряжения источника ω, либо изменением величины индуктивности L, либо изменением величины емкости С.
При резонансе входная проводимость цепи минимальна и равна активной проводимости G, а ток I достигает минимального значения. Токи в реактивных элементах при резонансе 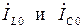 одинаковы по величине и противоположны по фазе, поэтому на векторной диаграмме, изображающей токи в элементах (рис. 2.12,б), они компенсируют друг друга, а входной ток
одинаковы по величине и противоположны по фазе, поэтому на векторной диаграмме, изображающей токи в элементах (рис. 2.12,б), они компенсируют друг друга, а входной ток 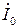 равен току в активной проводимости
равен току в активной проводимости 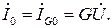 При этом токи в реактивных элементах могут превосходить ток в неразветвленной части цепи.
При этом токи в реактивных элементах могут превосходить ток в неразветвленной части цепи.
Проводимости реактивных элементов при резонансной частоте называют волновой проводимостью γ
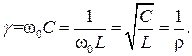
Отношение активной проводимости к волновой называется затуханием цепи d=g/ γ. Затухание цепи с параллельным соединением равно также отношению тока I 0 в неразветвленной части цепи к току в индуктивности или емкости:
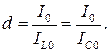
Чем меньше затухание контура, тем больше ток при резонансе в реактивных элементах по сравнению с током в неразветвленной цепи (входным током).
Резонансная кривая тока в параллельном контуре приведена на рис. 2.13. Такой же вид кривая тока имеет и в случае изменения величины емкости или индуктивности при неизменной частоте.
При резонансе токов также происходит обмен энергией между индуктивностью и емкостью, а энергия от источника покрывает только потери энергии в активном сопротивлении цепи. Электрические колебания в параллельных ветвях, обусловленные колебаниями энергии, могут быть очень интенсивными, а токи в реактивных элементах очень большими при относительно небольшом токе сети.
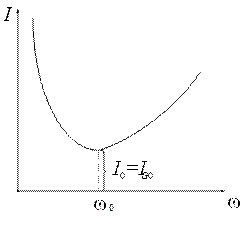
Рис. 2.13. Резонансная кривая тока
Для определения резонансной частоты при смешанном соединении элементов R, L, C необходимо найти комплекс входного сопротивления цепи и приравнять нулю его мнимую часть. Если в результате вычислений получается комплексное значение резонансной частоты, то резонанс при таком сочетании параметров невозможен.
2.2. Лабораторная работа №3
 2015-02-18
2015-02-18 10955
10955








