Теорема Тейлора (о разложении функции в степенной ряд).
Функция, аналитическая в области комплексных чисел D, в окрестности каждой точки z 0 этой области представляется в виде степенного ряда:
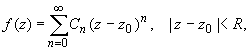 (1)
(1)
радиус сходимости R которого не меньше, чем расстояние от точки z 0 до границы области D.
Такой степенной ряд называется рядом Тейлора.
Коэффициенты ряда Тейлора вычисляются по формуле:
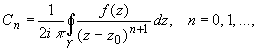 (2)
(2)
где 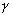 - произвольный контур, принадлежащий области D и охватывающий точку z 0 (в частности,
- произвольный контур, принадлежащий области D и охватывающий точку z 0 (в частности, 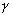 - окружность
- окружность 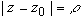 ), или по формуле:
), или по формуле:
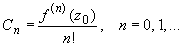 (3)
(3)
Радиус сходимости ряда Тейлора равен расстоянию от точки z 0 до ближайшей особой точки функции.
Для вычисления радиуса сходимости ряда Тейлора можно также использовать формулы:
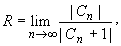
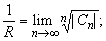
Основные разложения.
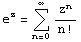 (z принадлежит области комплексных чисел);
(z принадлежит области комплексных чисел);
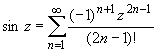 (z принадлежит области комплексных чисел);
(z принадлежит области комплексных чисел);
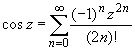 (z принадлежит области комплексных чисел);
(z принадлежит области комплексных чисел);
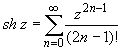 (z принадлежит области комплексных чисел);
(z принадлежит области комплексных чисел);
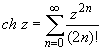 (z принадлежит области комплексных чисел);
(z принадлежит области комплексных чисел);
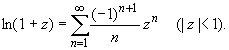
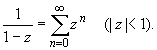
33.
34. Изолированные особые точки. Ряд Лорана.
Точка z 0, принадлежащая области комплексных чисел, называется изолированной особой точкой функции f (z), если 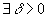 такая, что f (z) является однозначной аналитической функцией в
такая, что f (z) является однозначной аналитической функцией в 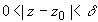 (в самой точке аналитичность f (z) нарушается).
(в самой точке аналитичность f (z) нарушается).
Изолированная особая точка z 0 функции f (z) называется:
· устранимой особой точкой, если 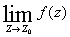 существует и конечен;
существует и конечен;
· полюсом, если 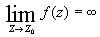 ;
;
· существенно особой точкой, если 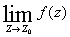 не существует.
не существует.
· Теорема Лорана (о разложении функции в ряд по целым степеням).
Функция f (z), аналитическая в кольце
r < | z - z 0 | < R, 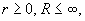
представляется в этом кольце сходящимся рядом по целым степеням, т.е. имеет место равенство:
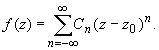 (1)
(1)
Коэффициенты ряда вычисляются по формуле: 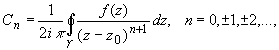 (2)
(2)
где 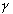 - произвольный контур, принадлежащий кольцу и охватывающий точку z 0; в частности,
- произвольный контур, принадлежащий кольцу и охватывающий точку z 0; в частности,
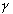 - окружность
- окружность 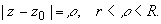
Ряд (1), коэффициенты которого вычисляются по формуле (2), называется рядом Лорана функции f (z).
Совокупность членов ряда с неотрицательными степенями 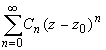 называется правильной частью ряда Лорана, члены с отрицательными степенями образуют главную часть ряда Лорана:
называется правильной частью ряда Лорана, члены с отрицательными степенями образуют главную часть ряда Лорана:
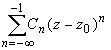 или
или 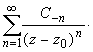
Для коэффициентов ряда имеет место формула оценки коэффициентов - неравенство Коши:
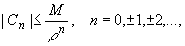 где
где 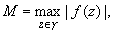
- радиус контура интегрирования в формуле (2).
На границах кольца сходимости ряда Лорана есть хотя бы по одной особой точке функции f (z) - его суммы.
Частными случаями рядов Лорана являются разложения функции в окрестности особой точки z 0 (r = 0) и в окрестности бесконечно удаленной точки (z 0 = 0, 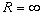 ).
).
При построении разложений в ряд Лорана используются разложения в степенные ряды (ряды Тейлора), используются основные разложения и арифметические операции со сходящимися рядами.
Для того чтобы особая точка функции f (z) была ее устранимой особой точкой, необходимо и достаточно, чтобы в разложении функции в ряд Лорана в окрестности этой точки отсутствовала главная часть. Это означает, что если z 0 - устранимая особая точка, то ряд Лорана функции f (z) имеет вид: 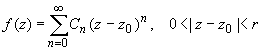 (1)
(1)
для z 0 - конечной точки, принадлежащей области комплексных чисел.
Для того чтобы особая точка функции была полюсом, необходимо и достаточно, чтобы главная часть ряда Лорана функции в окрестности этой точки содержала конечное число членов.
Ряд Лорана функции f (z) в случае z 0-полюс имеет вид:
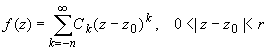 (2)
(2)
если z 0 принадлежит области комплексных чисел.
Номер старшего члена главной части ряда Лорана функции в ее разложении в окрестности полюса называется порядком полюса.
Так, точка z 0 является полюсом порядка n функции f (z), если в разложении (2) 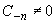 , Ck = 0 при k < - n.
, Ck = 0 при k < - n.
Для того чтобы особая точка функции была ее существенно особой точкой, необходимо и достаточно, чтобы главная часть ряда Лорана функции в окрестности этой точки содержала бесконечное число членов. Ряд Лорана функции f (z) в случае z 0 - существенно особой точки имеет вид: 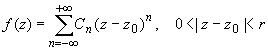 (3)
(3)
если z 0 принадлежит области комплексных чисел.
35. Вычеты, их вычисление. Основная теорема теории вычетов.
Вычетом функции 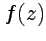 в изолированной точке
в изолированной точке 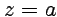 называется интеграл
называется интеграл
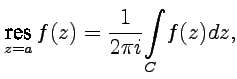 |
где 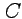 - замкнутый контур, содержащий одну особую точку
- замкнутый контур, содержащий одну особую точку 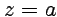 .
.
Вычетом функции 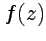 в точке
в точке 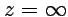 называется интеграл
называется интеграл
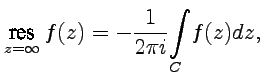 Основные формулы для нахождения вычетов: 1. Если а – устранимая особая точка для функции f (z), то Основные формулы для нахождения вычетов: 1. Если а – устранимая особая точка для функции f (z), то 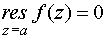 2. Если а – полюс первого порядка функции f (z), то 2. Если а – полюс первого порядка функции f (z), то 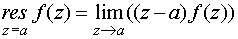 В частности, если В частности, если 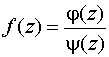 ,где (z) и(z) – регулярные в точке а функции, причем а ,где (z) и(z) – регулярные в точке а функции, причем а 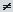 , а) , а) 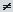 а) а) 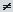 , то точка а является простым полюсом функции f (z) и , то точка а является простым полюсом функции f (z) и 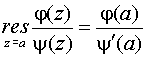 3. Если точка а – полюс порядка т 3. Если точка а – полюс порядка т 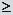 1 для функции f (z), то 1 для функции f (z), то 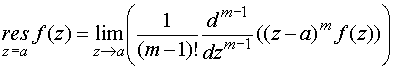 . В частности, если . В частности, если 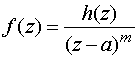 , h (z) – регулярна в точке а, h (а) , h (z) – регулярна в точке а, h (а) 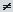 0, то справедлива формула 0, то справедлива формула 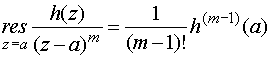 . 4. Если f (z) регулярна в точке z = . 4. Если f (z) регулярна в точке z = 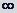 , то , то 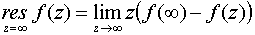 ,где ,где 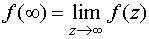 . 5. Если функция f (z) представима в виде . 5. Если функция f (z) представима в виде 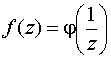 ,где функция ,где функция 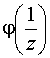 регулярна в точке =0, то регулярна в точке =0, то 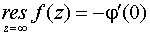 Приведем еще одну, важную для практического вычисления вычетов теорему. Теорема. Если z=a (а Приведем еще одну, важную для практического вычисления вычетов теорему. Теорема. Если z=a (а 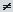 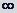 ) – изолированная особая точка однозначного характера функции f (z), то ) – изолированная особая точка однозначного характера функции f (z), то 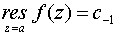 ,где с–1 – коэффициент при ,где с–1 – коэффициент при 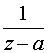 в ряде Лорана функции f (z) в окрестности точки z=a и в ряде Лорана функции f (z) в окрестности точки z=a и 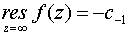 ,где с-1 – коэффициент при ,где с-1 – коэффициент при 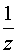 в ряде Лорана функции f (z) в окрестности точки z = в ряде Лорана функции f (z) в окрестности точки z = 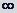 . . |
Основная теорема о вычетах: если функция 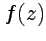 является аналитической всюду в замкнутой области
является аналитической всюду в замкнутой области 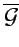 , за исключением конечного числа изолированных особых точек
, за исключением конечного числа изолированных особых точек 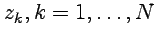 , лежащих внутри
, лежащих внутри 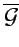 , то
, то
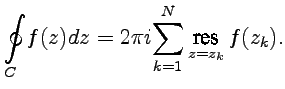 |
36. Вычисление интегралов с помощью вычетов
Пусть функция 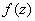 аналитична в верхней полуплоскости, включая действительную ось, за исключением конечного числа особых точек
аналитична в верхней полуплоскости, включая действительную ось, за исключением конечного числа особых точек 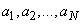 , лежащих в верхней полуплоскости. При этих условиях мы рассмотрим способы вычисления интегралов
, лежащих в верхней полуплоскости. При этих условиях мы рассмотрим способы вычисления интегралов
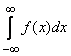 ,
, 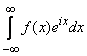 .
.
Теорема 1. Пусть функция 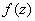 удовлетворяет перечисленным выше условиям и, кроме того,
удовлетворяет перечисленным выше условиям и, кроме того, 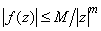 при
при 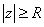 , где
, где 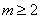 и
и 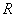 - достаточно большое число. Тогда
- достаточно большое число. Тогда
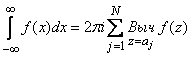 . (1)
. (1)
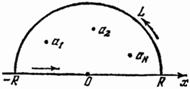
Доказательство. Опишем полуокружность 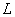 (ориентированную против часовой стрелки) радиуса
(ориентированную против часовой стрелки) радиуса 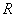 с центром в точке
с центром в точке 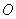 так, чтобы все особые точки функции
так, чтобы все особые точки функции 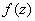 попали внутрь
попали внутрь 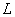 (рис. 149). В силу теоремы 1 § 6.13
(рис. 149). В силу теоремы 1 § 6.13
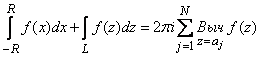 . (2)
. (2)
Так как 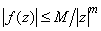 при
при 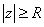 , то
, то
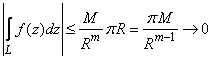 ,
, 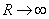
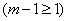 .
.
Переходя к пределу в равенстве (2) при 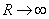 , получим (1).
, получим (1).
Теорема 2. Пусть функция 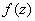 удовлетворяет условиям, отмеченным в начале параграфа и
удовлетворяет условиям, отмеченным в начале параграфа и 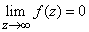 равномерно относительно
равномерно относительно 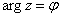 . Тогда
. Тогда
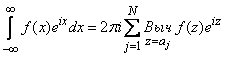 . (3)
. (3)
Доказательство. Так же как при доказательстве теоремы 1, имеем
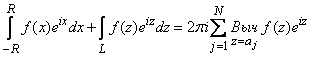 (4)
(4)
(функция 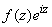 имеет те же особенности, что и
имеет те же особенности, что и 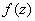 ).
).
Нам нужно доказать, что при 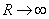 интеграл
интеграл 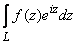 стремится к нулю. Имеем
стремится к нулю. Имеем
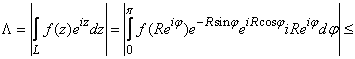
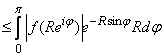 .
.
В силу условия теоремы 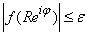 при
при 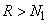 для всех
для всех 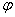 (
(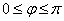 ) и достаточно большого
) и достаточно большого 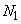 . Поэтому (
. Поэтому (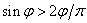 при
при 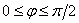 )
)

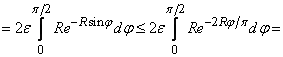
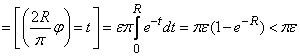
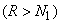 .
.
Переходя к пределу в (4), при 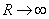 получаем (3).
получаем (3).
Если функция 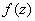 имеет особенности на действительной оси, то специальным построением контура интегрирования можно вычислить соответствующие интегралы, если они существуют.
имеет особенности на действительной оси, то специальным построением контура интегрирования можно вычислить соответствующие интегралы, если они существуют.
 2015-02-04
2015-02-04 2792
2792