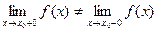Поскольку точки 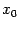 непрерывности функции
непрерывности функции 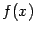 задаются условием
задаются условием 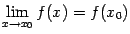 , то часть свойств функций, непрерывных в точке
, то часть свойств функций, непрерывных в точке 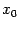 , следует непосредственно из свойств пределов. Сформулируем их в виде следующей теоремы.
, следует непосредственно из свойств пределов. Сформулируем их в виде следующей теоремы.
Теорема 3.1 Пусть функции 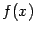 и
и 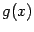 непрерывны в точке
непрерывны в точке 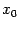 . Тогда функции
. Тогда функции 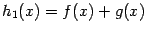 ,
, 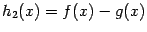 ,
, 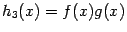 непрерывны в точке
непрерывны в точке 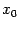 . Если
. Если 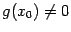 , то функция
, то функция 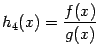 также непрерывна в точке
также непрерывна в точке 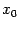 .
.
Доказательство. Оно сразу же следует из теорем о пределах 2.8, 2.9, 2.10 и следствия 2.5.
Как непосредственное следствие этой теоремы получается следующее
Предложение 3.3 Рассмотрим множество всех функций, определённых в некоторой фиксированной окрестности 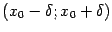 точки
точки 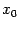 и непрерывных в этой точке. Тогда это множество
и непрерывных в этой точке. Тогда это множество 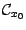 является линейным пространством, то есть замкнуто относительно сложения и умножения на постоянные:
является линейным пространством, то есть замкнуто относительно сложения и умножения на постоянные:

Доказательство. Действительно, постоянные 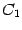 и
и 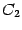 -- это непpеpывные функции (в любой точке); по пpедыдущей теоpеме тогда непpеpывны в точке
-- это непpеpывные функции (в любой точке); по пpедыдущей теоpеме тогда непpеpывны в точке 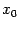 пpоизведения
пpоизведения 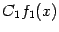 и
и 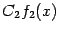 . Но тогда по этой же теоpеме непpеpывна в точке
. Но тогда по этой же теоpеме непpеpывна в точке 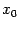 и сумма
и сумма 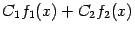 .
.
Теорема 3.2 Пусть функции 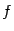 и
и 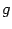 таковы, что существует композиция
таковы, что существует композиция 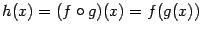 ,
, 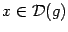 . Пусть функция
. Пусть функция 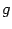 непрерывна в точке
непрерывна в точке 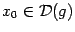 , а функция
, а функция 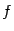 непрерывна в соответствующей точке
непрерывна в соответствующей точке 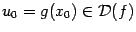 . Тогда композиция
. Тогда композиция 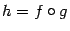 непрерывна в точке
непрерывна в точке 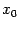 .
.
Доказательство. Заметим, что равенство 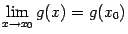 означает, что при
означает, что при 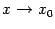 будет
будет 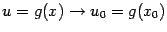 . Значит,
. Значит,
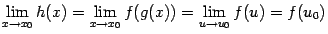
(последнее равенство следует из непрерывности функции 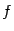 в точке
в точке 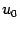 ). Значит,
). Значит,
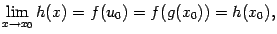
а это равенство означает, что композиция 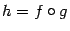 непрерывна в точке
непрерывна в точке 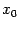 .
.
Заметим, что, очевидно, в предыдущих двух теоремах можно было бы заменить базу 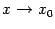 на односторонние базы
на односторонние базы 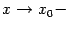 или
или 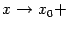 и получить аналогичные утверждения для непрерывности слева или справа:
и получить аналогичные утверждения для непрерывности слева или справа:
Теорема 3.3 Пусть функции 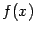 и
и 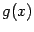 непрерывны слева (справа) в точке
непрерывны слева (справа) в точке 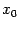 . Тогда функции
. Тогда функции 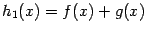 ,
, 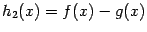 ,
, 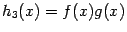 непрерывны слева (соотв. справа) в точке
непрерывны слева (соотв. справа) в точке 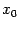 . Если
. Если 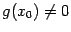 , то функция
, то функция 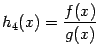 также непрерывна слева (спpава) в точке
также непрерывна слева (спpава) в точке 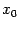 .
.
Теорема 3.4 Пусть функция 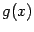 непрерывна слева (справа) в точке
непрерывна слева (справа) в точке 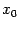 , а функция
, а функция 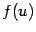 непрерывна в точке
непрерывна в точке 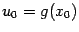 . Тогда композиция
. Тогда композиция 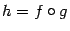 непрерывна слева (соотв. справа) в точке
непрерывна слева (соотв. справа) в точке 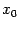 .
.
| Точки разрыва и их классификация |  |  |  |
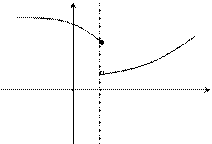
Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х0, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х0 является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной. Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом. Если односторонний предел (см. выше) 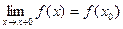 , то функция называется непрерывной справа. , то функция называется непрерывной справа.
х0 Если односторонний предел (см. выше)
х0 Определение. Точка х0 называется Точкой разрыва Функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке. Определение. Точка х0 называется Точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.
Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х0, достаточно того, что она определена слева и справа от нее. Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют Устранимой Точкой разрыва, но подробнее об этом поговорим ниже. Определение. Точка х0 называется Точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен. |
Свойства функций непрерывных на отрезке:
1. Теорема Вейерштрасса. Если функция непрерывна на отрезке, то она достигает на этом отрезке свои наибольшее и наименьшее значения.
2. Непрерывная на отрезке 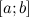 функция является ограниченной на этом отрезке.
функция является ограниченной на этом отрезке.
3. Теорема Больцано-Коши. Если функция 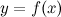 является непрерывной на отрезке
является непрерывной на отрезке 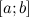 и принимает на концах этого отрезка неравные между собой значения, то есть
и принимает на концах этого отрезка неравные между собой значения, то есть 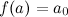 ,
, 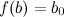 , то на этом отрезке функция принимает и все промежуточные значения между
, то на этом отрезке функция принимает и все промежуточные значения между 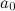 и
и 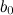 .
.
4. Если функция 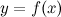 , которая непрерывна на некотором отрезке
, которая непрерывна на некотором отрезке 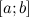 , принимает на концах отрезка значения разных знаков, то существует такая точка
, принимает на концах отрезка значения разных знаков, то существует такая точка 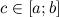 такая, что
такая, что 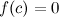 .
.
 2015-03-22
2015-03-22 1357
1357


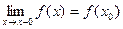 , то функция называется непрерывной слева.
, то функция называется непрерывной слева.