Пусть имеем скалярное поле, определяемое скалярной функцией U=f(M). Возьмем в поле точку М0 и выберем некоторое направление, определяемое вектором  . Возьмем в поле другую точку М1 так, чтобы вектор
. Возьмем в поле другую точку М1 так, чтобы вектор 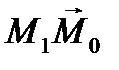 был параллелен вектору
был параллелен вектору  .
.
Обозначим через 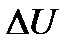 разность
разность 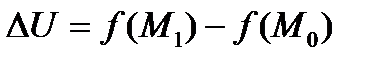 . А через
. А через 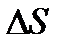 длину вектора
длину вектора 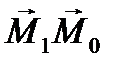 . Отношение
. Отношение 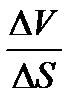 определяет среднюю скорость изменения скалярного поля на единицу длины по данному направлению.
определяет среднюю скорость изменения скалярного поля на единицу длины по данному направлению.
Будем стремить точку М1 к точке М0 так, чтобы вектор 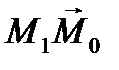 оставался все время коллиниарен вектору
оставался все время коллиниарен вектору 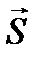 . При этом
. При этом 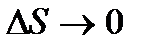 .
.

Определение 1.3. Если существует при 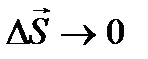 предел отношения
предел отношения 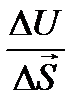 , то его называют производной функциеи U=f(M) в данной точке М0 по направлению
, то его называют производной функциеи U=f(M) в данной точке М0 по направлению 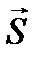 и обозначают символом
и обозначают символом  . Так что по определению
. Так что по определению
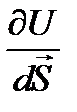 =
= 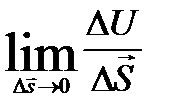 =
= 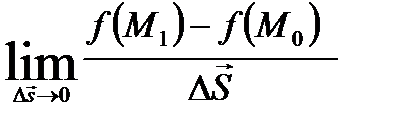 ,
, 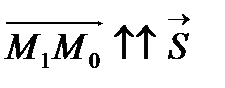 .
.
Это определение производной по направлению носит инвариантный характер, то есть не связано с выбором системы координат.
Пусть в пространстве введена декартова система координат и пусть функция f(M)=f(x,z,y) дифференцируема в точке М0(x0,y0,z0).Тогда
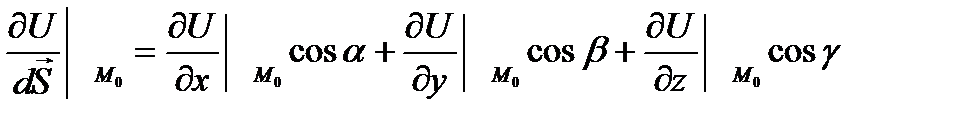 (1.3.)
(1.3.)
где cos 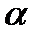 , cos
, cos 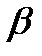 , cos
, cos  - направляющие косинусы вектора
- направляющие косинусы вектора 
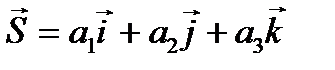 . Находятся по формулам
. Находятся по формулам
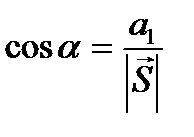 ,
, 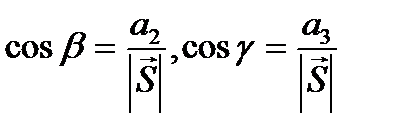 .
.  (1.4)
(1.4)
символы 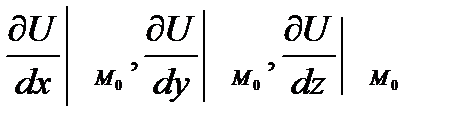 , означают, что частные производные берутся в точке М0.
, означают, что частные производные берутся в точке М0.
Пример 1.5. Найти производную скалярного поля U=x2+y2+z2 в точке М0(1;2;-1) в направлении вектора 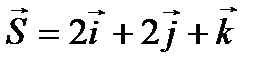 .
.
Решение. а) Находим направляющие косинусы вектора по формуле (1.4):
 =
= 
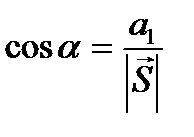 =
=  ,
, 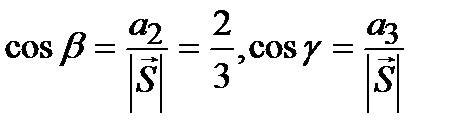 =
=  (1.5)
(1.5) 
б) Находим частные производные функции в точке М0(1;2;-1)
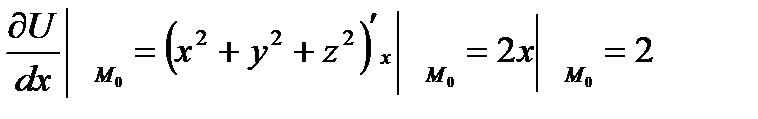
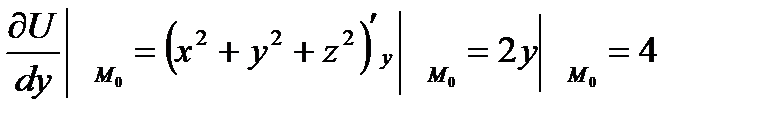 (1.6.)
(1.6.)

(1.5) и (1.6) подставляя в (1.3), получим

Пример 1.6. Найти производную скалярного поля U=xyz в точке М0(1;-1;1).
Решение. а) Находим направляющие косинусы вектора 
 =
= 
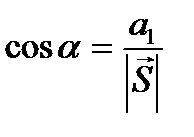 =
= 
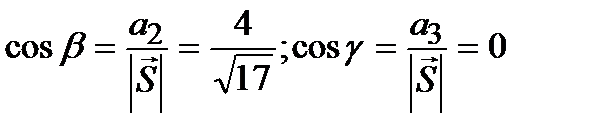 (1.7.)
(1.7.)
б) Находим частные производные функций в точке М0(1;-1;1).

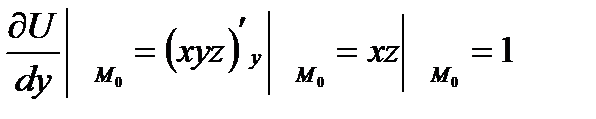 (1.8)
(1.8)
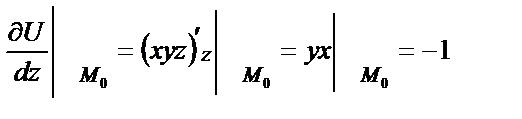
Используя формулы (1.3) и учитывая (1.7), (1.8) имеем
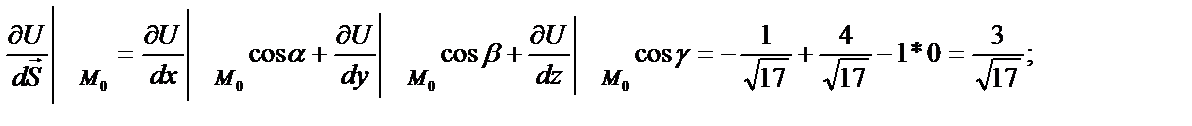 Для плоского поля U=f(x,y) производная по направлению
Для плоского поля U=f(x,y) производная по направлению 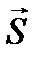 в точке М0(x0,y0,z0) будет равна
в точке М0(x0,y0,z0) будет равна
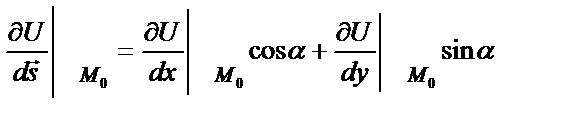 , (1.9)
, (1.9)
где 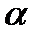 - угол, образованный вектором
- угол, образованный вектором 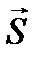 с осью ox.
с осью ox.
Пример1.7. Вычислить производную скалярного поля U=arctgxy в точке М0(1,1), принадлежащей параболе y=x2, по направлению этой кривой (в направлении возрастания абсциссы).
Решение. Направлением 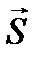 параболы у=х2 в точке М0(1,1) считается направление касательной к параболе в этой точке.
параболы у=х2 в точке М0(1,1) считается направление касательной к параболе в этой точке.
Пусть касательная 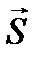 к кривой в точке М0 образует с осью ох угол
к кривой в точке М0 образует с осью ох угол 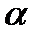 . Пусть
. Пусть 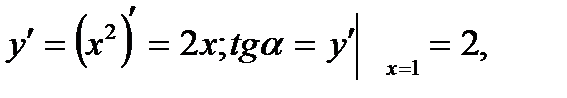 откуда направляющие косинусы касательной
откуда направляющие косинусы касательной 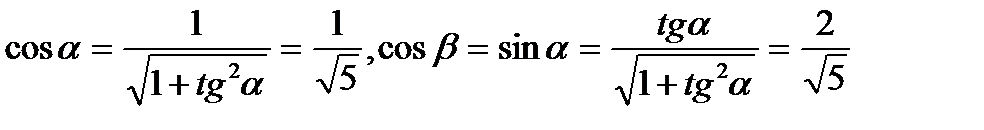 .
.
Значение частных производных данной функции U(x,y) в точке М0(1;1)

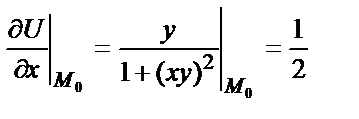 ;
; 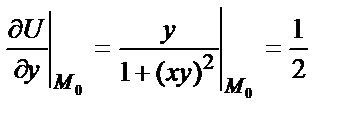 .
.
 2015-03-07
2015-03-07 8716
8716
