2.1. Уравнение вида 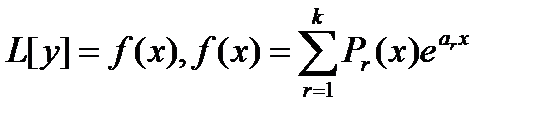 (Pr(x)-многочлен)
(Pr(x)-многочлен)
На основании Леммы 14.1 достаточно уметь находить частное решение, когда правая часть f(x) задана в виде
f(x)=Pm(x)eax=(Pmxm+Pmxm-1+…+P0)eαx
1.Пусть
F(k)=km+P1km-1+P2km-2+…Pn-1k+Pn=0 (14.3)
Характеристическое уравнение соответствующее однородному уравнению.
L[y]=0 (14.1)
И α –не является корнем характеристического уравнения, F(α)=0
Мы докажем, что в этом случае существует частное решение того же вида, что и правая часть, а именно
Y=Qm(x) (14.4)
Где Qm(x)=bmxm+bm-1xm-1+…+b1x+b0, рассматривая bm, bm-1,…,b1b0 как неизвестные.
Определим эти коэффициенты. Нетрудно заметить, что
L[Qm(x)eα.x]=Pm(x)eα.x
или
e-α.xL[Qm(x)eα.x]= Pm(x) (14.5)
вычислим левую часть, применяя формулу
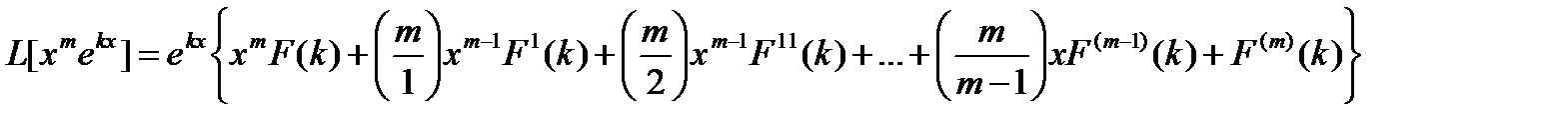 (14.6)
(14.6)
То есть
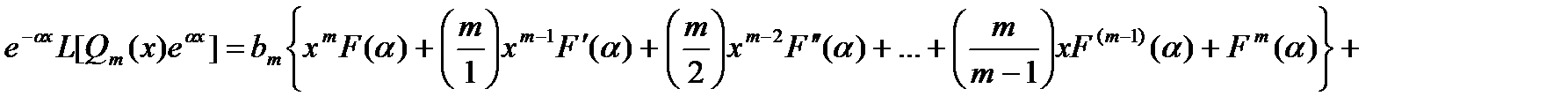
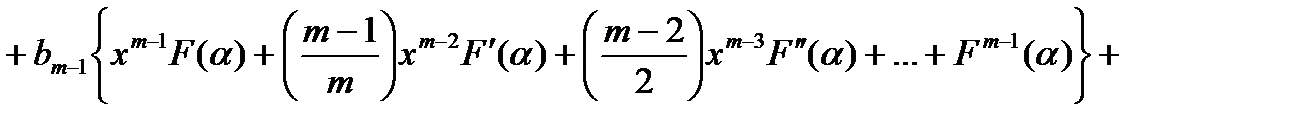
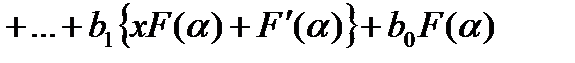 (14.7)
(14.7)
Приравнивая выражения (14,5) многочлену Pm(x) и отождествляя коэффициенты при одинаковых степенях x, получим m+1 уравнений c m+1 неизвестными b0,b1,…,bn,
bmF(α)=Pm
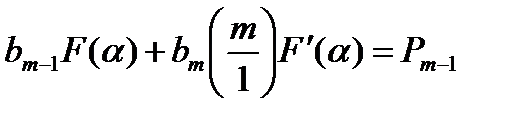
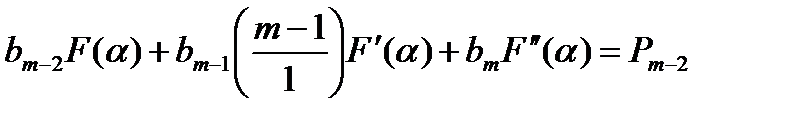 (14.8)
(14.8)
……………………………………………………..=…………
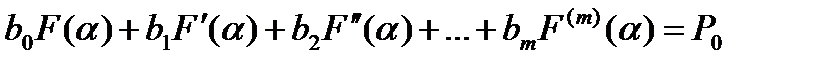
Так как по условию α не является корнем характеристического уравнения, то F(α)=0
Система (14.8) дает возможность последовательно вычислить
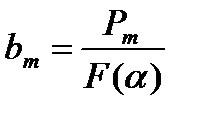
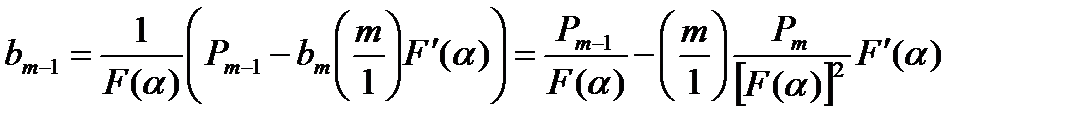 (14.9)
(14.9)
И так далее.
Таким образом, мы находим искомое частное решение (14.4). [Разрешимость системы (14.8) относительно b0,b1,…,bm, можно сразу увидеть из того, что ее определитель равен [F(α)]m+1=0].
Пример14.1: Найти решение уравнения
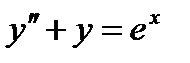 (14.10)
(14.10)
Решение: В нашем случае f(x)=Pm(X)eαx, m=0, α=0, P0=0. Число α=1, не является корнем характеристического уравнения F(k)=k2+1=0, F(1)=12+1=20, поэтому частное решение ищем в виде
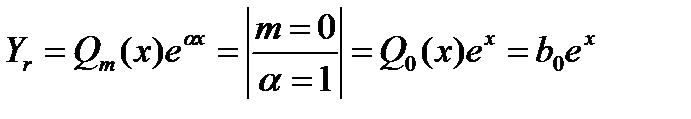
Согласно (14.8), имеем
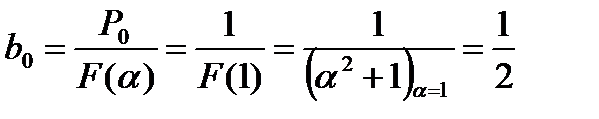
Следовательно
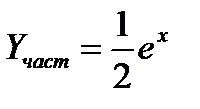
Общее решение уравнение (14.9) имеет вид
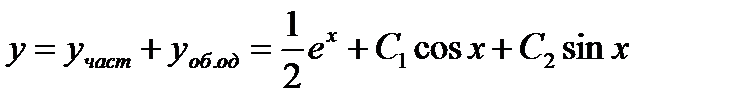
1. Пусть теперь α является корнем характеристического уравнения кратности 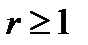 . Тогда
. Тогда
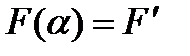
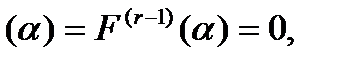
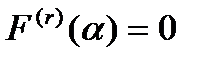 . Формула (14.6) показывает, что в это случае
. Формула (14.6) показывает, что в это случае
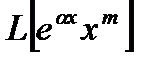 есть произведение
есть произведение 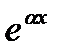 на многочлен степени
на многочлен степени 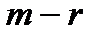 . Чтобы получить в результате подстановки в левую часть уравнения
. Чтобы получить в результате подстановки в левую часть уравнения 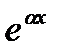 , умноженное на многочлен степени m, естественно искать частное решение в этом случае в виде
, умноженное на многочлен степени m, естественно искать частное решение в этом случае в виде
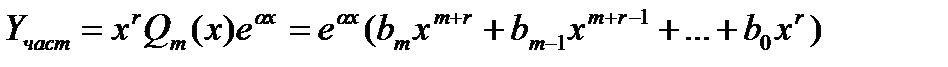 (14.11)
(14.11)
Подставляя это выражение в уравнение
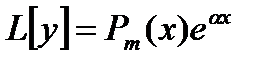
И требуя, чтобы (14.11) было решением уравнения, мы приходим к условию
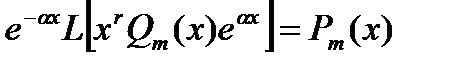 (14.12)
(14.12)
Вычисляя левую часть, пользуясь формулой (14.6) и учитывая, что 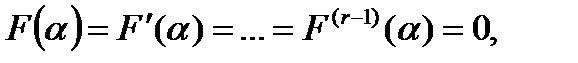
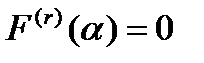 , имеем
, имеем
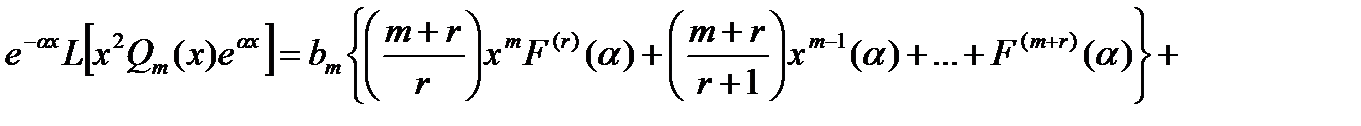
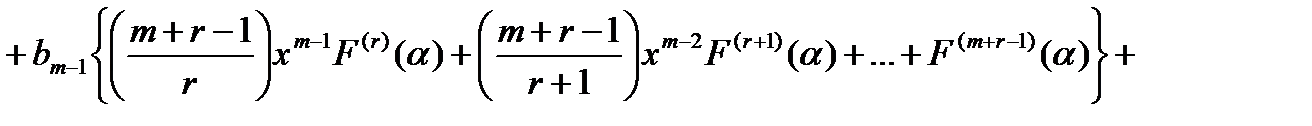 (14.13)
(14.13)
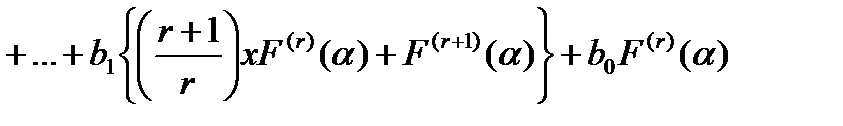
Подставляя выражение (14.13) в равенство (14.12) и приравнивая после этого коэффициенты при одинаковых степенях х в обеих частях равенства (14.12), опять получаем систему (m+1) уравнений для определения b0,b1,b2…,bm,
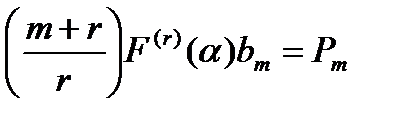
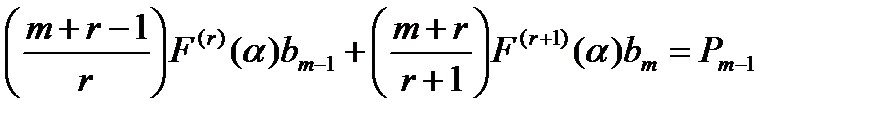
………………………………………………………………………………. (14.14)
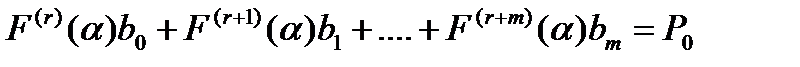
Определитель системы (14.14) равен
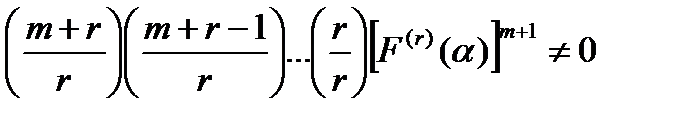
Поэтому все неизвестные 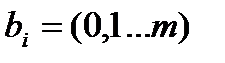 определяются однозначно, и мы получаем решение вида (14.11).
определяются однозначно, и мы получаем решение вида (14.11).
Теорема 14.1 Частное решение линейного уравнения с постоянными коэффициентами и с правой частью вида 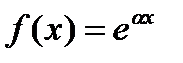
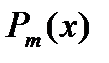 может быть найдено в виде
может быть найдено в виде 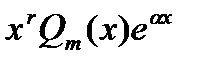 где
где 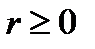 есть кратность α характеристического уравнения, Qm есть многочлен той же степени, что Pm(x).
есть кратность α характеристического уравнения, Qm есть многочлен той же степени, что Pm(x).
Пример 14.2: Решить уравнение 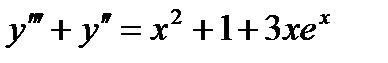
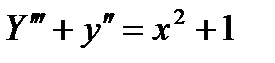 ,
, 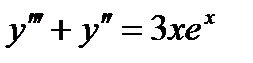
Характеристического уравнение очевидно имеет вид 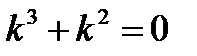 , его корни
, его корни 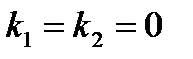 ,
, 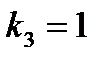
Рассмотрим сначала первое уравнение; в правой части нет показательного множителя, следовательно α=0, но нуль есть двух кратный корень характеристического уравнения. Тогда, согласно изложенному выше, должны искать частное решение в виде

Находим
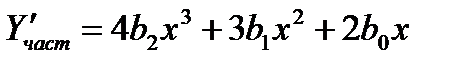
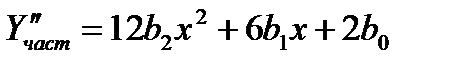
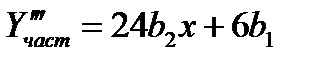
Подставляя в уравнение, получим:
24b2x+6b1+12b2x2+6b1x+2b0=x2+1
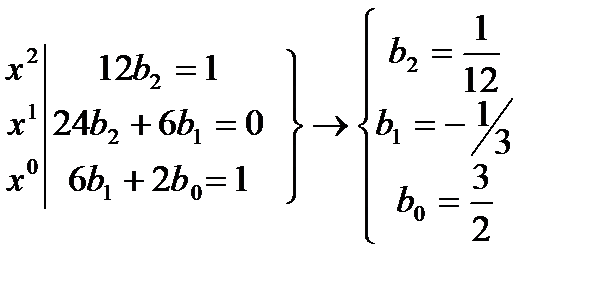
Следовательно
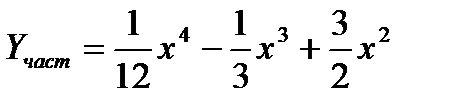
Переходим ко второму уравнению. Здесь α=1 не является корнем характеристического уравнения. Ищем частное решение в виде
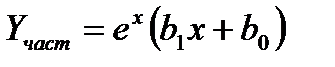 находим
находим 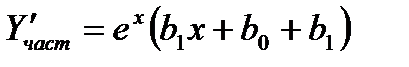
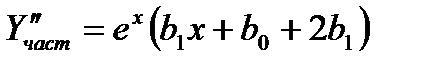 ,
, 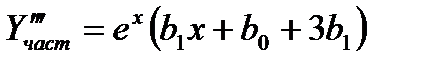
Подставляя в уравнение, имеем
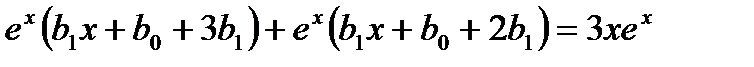
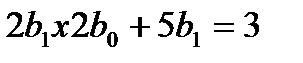
Приравниваем коэффициенты.
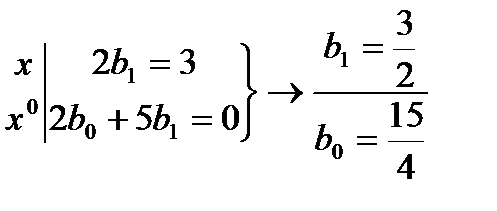
Искомое значение 
Общее решение данного уравнения, есть
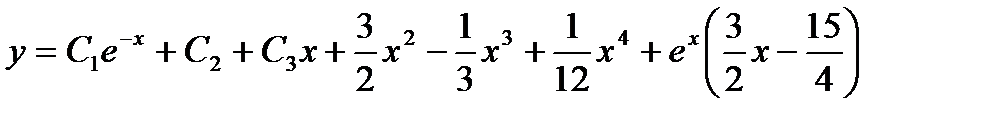
Пусть правая часть уравнений (14.1) имеет вид
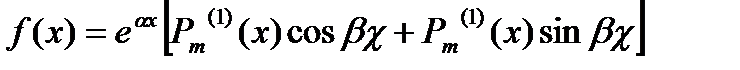
И в частности
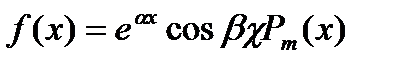 или
или 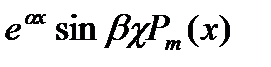
Где 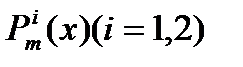 многочлен степени m, а α и β – действительные числа. Заметим, что cosβx, sinβx выражается линейно через показательные функции eiβx, e-iβx
многочлен степени m, а α и β – действительные числа. Заметим, что cosβx, sinβx выражается линейно через показательные функции eiβx, e-iβx
После замены тригонометрических функций показательными это выражения обратится в такое
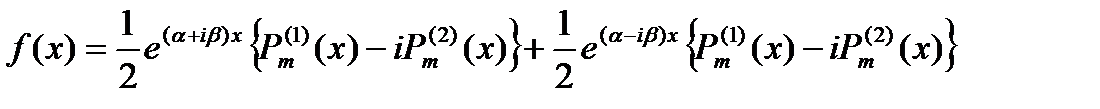
В частности
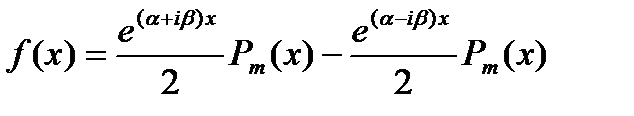
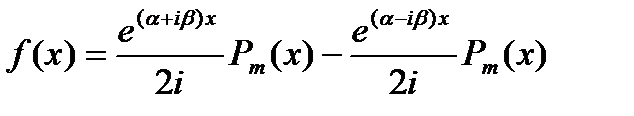
В силу пункта 1,2 мы должны искать частное решение в виде
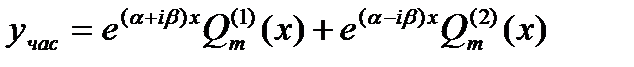 (14.15)
(14.15)
Если 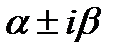 суть корня характеристического уравнения кратности r. Легко видеть, что системы уравнений (14.8) или (14.14) для определения коэффициентов многочлена
суть корня характеристического уравнения кратности r. Легко видеть, что системы уравнений (14.8) или (14.14) для определения коэффициентов многочлена 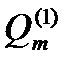 соответствующая система для
соответствующая система для 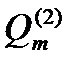 получается переходам к комплексным сопряженным значениям коэффициентов уравнений, следовательно, коэффициенты многочлена
получается переходам к комплексным сопряженным значениям коэффициентов уравнений, следовательно, коэффициенты многочлена 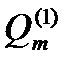 окажутся комплексными сопряженными с соответствующими
окажутся комплексными сопряженными с соответствующими 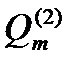 .
.
Поэтому, отделяя действительную часть от мнимой части, мы получим: если
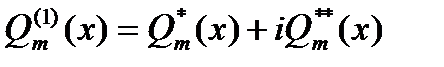 то
то 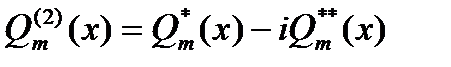 . Подставляя эти многочлены в выражение (14.15) и переходя от показательных функций к тригонометрическим, находим искомое выражение
. Подставляя эти многочлены в выражение (14.15) и переходя от показательных функций к тригонометрическим, находим искомое выражение
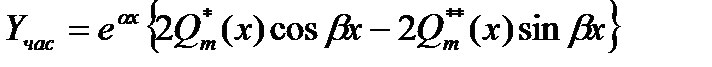
Это выражение не содержит комплексных величин. В случае, если 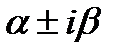 суть корня характеристического уравнения кратности r, то частное решение ищется в виде
суть корня характеристического уравнения кратности r, то частное решение ищется в виде
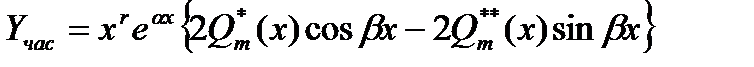
Теорема 14.2 Частное решение линейного уравнения с постоянными коэффициентами и с правой частью вида
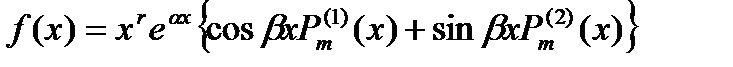
Можно найти в форме
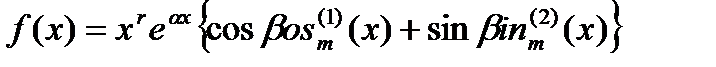
где 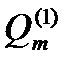 (х) и
(х) и 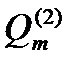 (х) многочлены той же степени, что
(х) многочлены той же степени, что 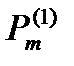 и
и 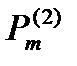 (или наибольшей, если эти степени не равны), а
(или наибольшей, если эти степени не равны), а 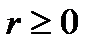 есть кратность корня
есть кратность корня 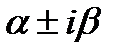 характеристического уравнения.
характеристического уравнения.
На практике опять пишут многочлены 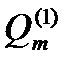 (х) и
(х) и 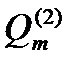 (х) с неопределенными коэффициентами, подставляя в уравнение и приравнивают коэффициентами, подставляя в уравнение и приравнивают коэффициенты в обеих частях при выражениях вида х1
(х) с неопределенными коэффициентами, подставляя в уравнение и приравнивают коэффициентами, подставляя в уравнение и приравнивают коэффициенты в обеих частях при выражениях вида х1 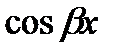 и
и 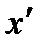
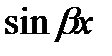

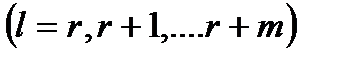 . Впрочем, иногда удобно производить вычисления и с иными показателями.
. Впрочем, иногда удобно производить вычисления и с иными показателями.
Пример 14.3: Проинтегрировать уравнение 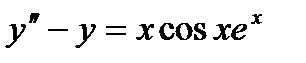
Решение: Характеристическое уравнение имеет вид 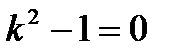 ,
, 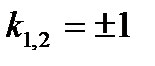 то, есть выражения
то, есть выражения 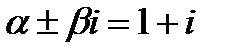 не является корнем характеристического уравнения
не является корнем характеристического уравнения 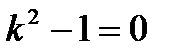 , поэтому частное решение ищем следующим образом:
, поэтому частное решение ищем следующим образом:
Представляем правую часть в виде
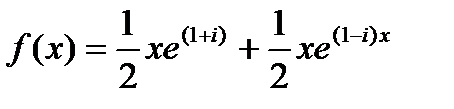
И ищем частное решение уравнения 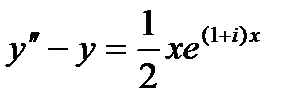 в форме
в форме 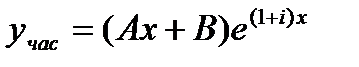
Имеем
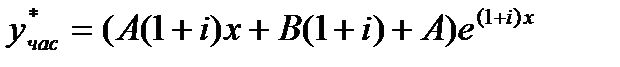
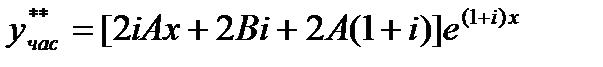
Подстановка в уравнение дает
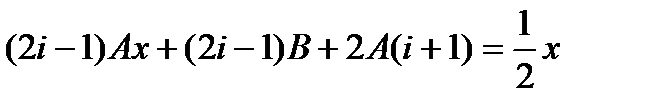
Откуда
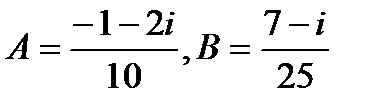
Итак,
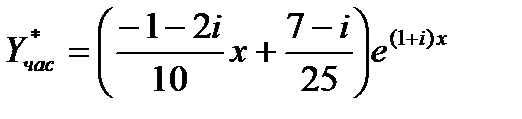
Решение 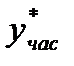 уравнения
уравнения 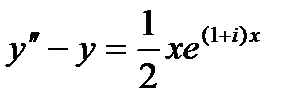 будет комплексным сопряженным
будет комплексным сопряженным 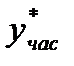

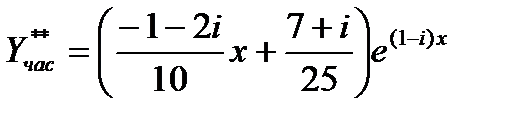
Складывая 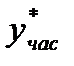 и
и 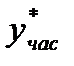 и переходя к тригонометрическим функциям, получаем частное решение заданного уравнения в виде
и переходя к тригонометрическим функциям, получаем частное решение заданного уравнения в виде
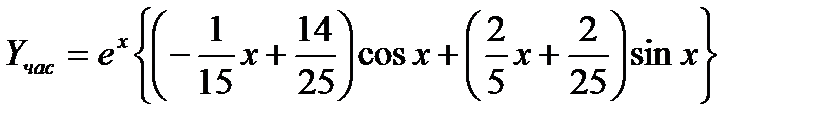
Тогда общее решение имеет вид
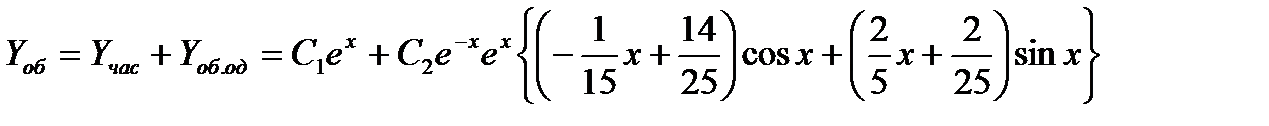
частное решение рассматриваемых задач можно искать в виде
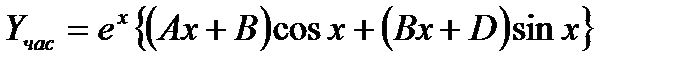
Пример 14.4:Найти общее решение уравнение упругих колебаний без сопротивления при наличии возмущающий периодической силы имеет вид
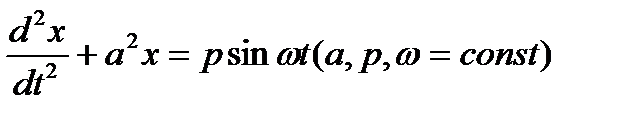
Решение: Составим характеристическое уравнение, соответствующему однородному уравнению 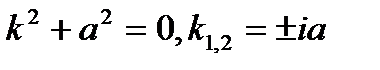 так как
так как 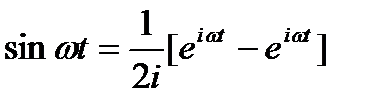 следовательно в силу Леммы 14.1 имеем:
следовательно в силу Леммы 14.1 имеем:
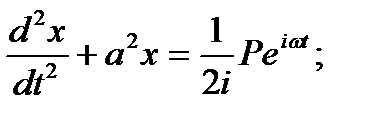
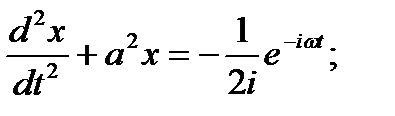
Следовательно, возможны два случая
1.ω=а. (Частота возмущающей силы не равна частоте собственных колебаний системы)
Тогда частное решение должно иметь вид
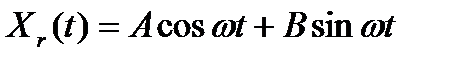
И находим 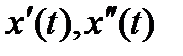
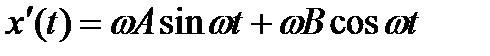
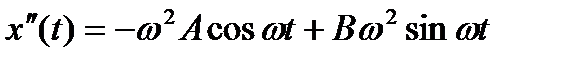
Подставляя в уравнение имеем
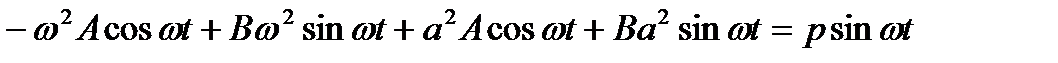
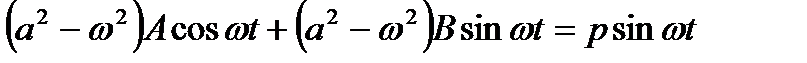
Откуда
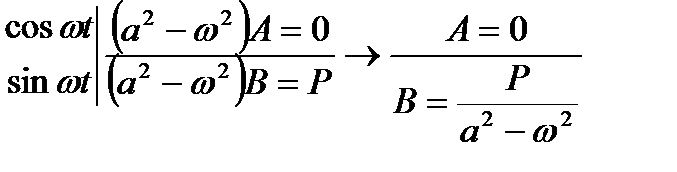
Следовательно, общее решение имеет вид
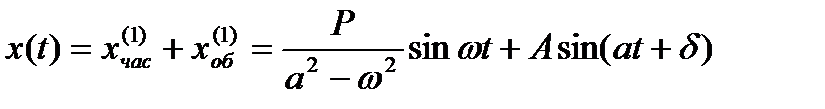
2. ω=а. Частное решение надо искать в виде
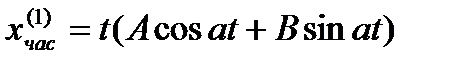
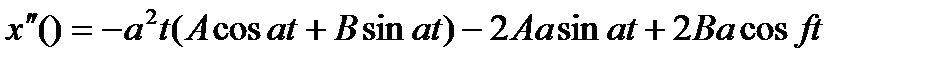
Подставляя в уравнение, находим 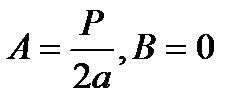
Общее решение уравнения имеет вид
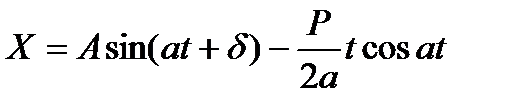
Рассмотри один важный частный случай.
Пусть правая часть линейного уравнения (14.1) имеет вид
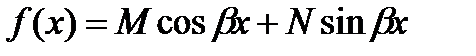
Где М и N-постоянные числа
А) Если 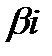 не является корнем характеристического уравнения, то частное решение следует ищется в виде
не является корнем характеристического уравнения, то частное решение следует ищется в виде
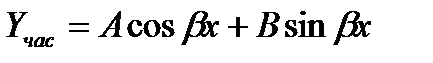
Б) Если 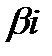 является корнем кратности
является корнем кратности 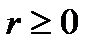 характеристического уравнения, то частное решение искать в виде
характеристического уравнения, то частное решение искать в виде

 2015-03-07
2015-03-07 810
810








