2015-03-20
905
Данные по среднемесячной начисленной заработной плате работников организаций отрасли приняты по данным официальной статистики: Официальная статистика / Рынок труда, занятость и заработная плата / Заработная плата / Затраты на рабочую силу и заработная плата / Среднемесячная номинальная начисленная заработная плата по видам экономической деятельности.
Данные по среднеотраслевой заработной плате приведены в Таблице 1.4. Динамика среднеотраслевой заработной платы по годам приведена на рис.1.3.
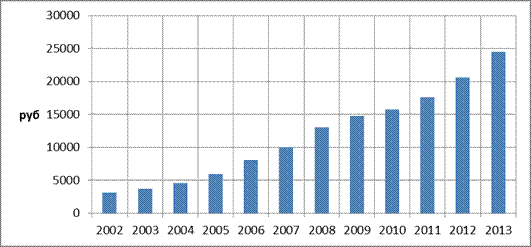
Рис.1.3. Среднеотраслевая заработная плата.
Вывод. За период 2002-2013 год среднеотраслевая заработная плата выросла в 7,8 раз. За период 2012-2013 год рост заработной платы составил 18%.
Таблица 1.4.
Средняя номинальная начисленная заработная плата работников отрасли, рублей
| 3141,3 | 3662,6 | 5905,6 | 8059,9 | 10036,6 | 13048,6 | 14819,5 | 15723,8 | 17544,5 | 20640,7 | 24438,6 |
Таблица 1.5.
Описательная статистика среднемесячной заработной платы работников сельского хозяйства
|
|
|
| Среднее | 7722,483 |
| Стандартная ошибка | 1389,234 |
| Медиана | 7309,3 |
| Мода | #Н/Д |
| Стандартное отклонение | 4812,449 |
| Дисперсия выборки | |
| Эксцесс | -1,31358 |
| Асимметричность | 0,344153 |
| Интервал | 13847,6 |
| Минимум | 1876,4 |
| Максимум | |
| Сумма | 92669,8 |
| Счет |
Проверим, какому закону статистическому распределения не противоречит выборка среднемесячной заработной платы. От этого зависит приемлемость корреляционного и регрессионного анализа, критериев сравнения. В аналитической статистике эта процедура называется проверкой соответствия выборочного распределения теоретическому, в данном случае, нормальному.
Необходимо проверить сложную гипотезу о проверке принадлежности выборочного распределения нормальному закону, сложную, потому что оценки параметров нормального распределения определены по той же выборке, по которой проверяют согласие. При проверке сложных гипотез непараметрические критерии оказываются более мощными. и уже при n =15-20 можно, не опасаясь больших ошибок, пользоваться этими предельными законами при анализе данных. Мощность непараметрических критериев при проверке сложных гипотез при тех же объемах выборок n всегда существенно выше, чем при проверке простых. Критерий проверки – критерий Крамера-Мизеса-Смирнова (асимптотический непараметрический критерий).
Выполним описательную статистику выборки среднемесячной заработной платы, приведенной в Таблице 1.4. Определим статистические оценки выборки. Для этого используем надстройку Данные / Анализ данных / Описательная статистика. Результаты приведены в Таблице 1.5.
Вычисления по критерию приведены в Таблице 1.6.
|
|
|
Таблица 1.6.
Проверка соответствия выборочных данных по среднемесячной заработной плате нормальному закону распределения
| Ранг, j | x |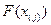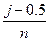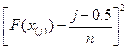 
| 
| 
|
| 1876,4 | 0,112224333 | 0,041667 | 0,004978384 | |
| 2339,8 | 0,131678549 | 0,125 | 4,4603E-05 | |
| 3015,4 | 0,164011031 | 0,208333 | 0,001964466 | |
| 3646,2 | 0,198489492 | 0,291667 | 0,008681986 | |
| 4568,7 | 0,256124889 | 0,375 | 0,014131292 | |
| 6143,8 | 0,371440106 | 0,458333 | 0,007550433 | |
| 8474,8 | 0,562112445 | 0,541667 | 0,00041803 | |
| 9619,2 | 0,653256416 | 0,625 | 0,000798425 | |
| 10668,1 | 0,729758486 | 0,708333 | 0,000459037 | |
| 0,837751991 | 0,791667 | 0,002123857 | ||
| 14129,4 | 0,908458387 | 0,875 | 0,001119464 | |
| 0,9518108 | 0,958333 | 4,25434E-05 | ||
| сумма | 0,042312521 | |||
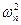| 0,049256965 | |||
| lnN | 0,476582533 | |||
| р | 0,523417467 |
В столбце 2 данные ранжированы в порядке возрастания. В столбце 3 вычислена функция НОРМРАСП с параметрами х – текущее значение столбца 2, среднее значение и стандартное отклонение из Таблицы 1.6, интегральная «1». В столбце 4 вычисляется значение 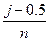, в котором j – ранг. Значения столбца 5 (квадрат разностей) суммируются.
Расчетное значение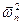 
статистики 
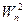вычисляется по формуле:
,
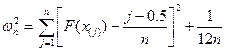где x(j) – j -тый элемент упорядоченной выборки; F(х) – гипотетическая функция распределения (нормальное распределение).
Значения столбца 5 суммируют. От найденного расчетного значения статистики 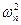вычисляют логарифмически нормальное распределение с параметрами ЛОГНОРМРАСП 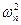; -2,9794; 0,5330). Вероятность соответствия выборочного распределения нормальному р=1-LnN.
Гипотезу о согласии не отвергают, если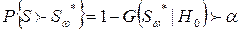 
, где a - принятый уровень значимости, обычно a=0,05.
Вывод. Выборка среднемесячной заработной платы с вероятностью 52% не противоречит нормальному закону распределения. К ней можно применять аппарат корреляционного и регрессионного анализа.
Выясним, есть ли статистическая связь между валовой добавленной стоимостью отрасли и среднемесячной заработной платой его работников.
Корреляционный анализ позволяет определить степень зависимости, сопряженности между двумя и более признаками. Корреляционная связь проявляется не в каждом конкретном случае, а в массе наблюдений. Линейная корреляционная связь (прямая и обратная) измеряется коэффициентом корреляции. Диаграмма рассеяния приведена на рис.1.4.
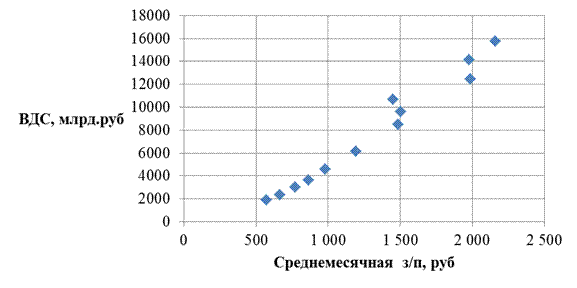
Рис.1.4. Диаграмма рассеяния «ВВП отрасли» - «Среднемесячная зарплата работников».
Коэффициент корреляции между этими величинами, вычисленный с помощью функции КОРРЕЛ равен 0,987. Этот коэффициент корреляции подразумевает, что выборки подчинены нормальному закону распределения.
Так как оценка тесноты связи с помощью коэффициента корреляции проводилась на основании ограниченной информации (наблюдения всего за 12 лет с 2002 по 2013) то необходимо выполнить оценку значимости линейного коэффициента корреляции. Оценка значимости коэффициента корреляции при малых объемах выборки выполняется с использованием t-критерия Стьюдента. При этом фактическое (наблюдаемое) значение определяется по формуле:
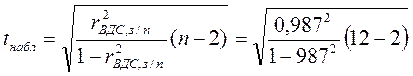=19,78
Вычисленное значение сравниваем с критическим значением t-критерия, которое вычисляем с помощью статистический функции СТЬЮРАСПРОБР(0,05; 10) с учетом заданного уровня значимости a=0.05 и числа степеней свободы n-2=12-2=10 t-табличное =2,364. Поскольку выполняется неравенство tнабл> tтабл, полученное значение коэффициента корреляции признаем значимым.
Вывод. Статистически достоверно есть корреляционная связь между валовой добавленной стоимостью и среднемесячной заработной платой. Степень линейной корреляционной связи сильная, так как значение коэффициента корреляции близко к 1. Положительное значение коэффициента говорит о том, что с ростом добавленной стоимости по отрасли растет и среднемесячная заработная плата.
