Определение. Внешним углом называется угол, смежный
с каким-нибудь углом треугольника.
Теорема. Внешний угол треугольника равен сумме двух
внутренних углов, не смежных с ним.
Доказательство. Пусть АВС – данный треугольник.
По теореме о сумме углов треугольников ∠A+∠В+∠C=180°, значит, ∠А + ∠В = 180°-∠С,
а 180°-∠С не что иное, как градусная мера внешнего угла при вершине С.
Теорема доказана.
Теорема. Сумма внешних углов n-угольника (взятых по одному при каждой вершине) равна 360°.
Доказательство. Из теоремы о сумме углов выпуклого n-угольника следует:
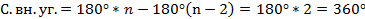
Теорема доказана.
2. 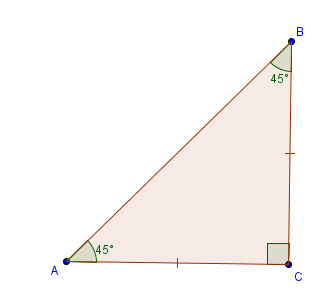 Нахождение значений синуса, косинуса и тангенса угла в 45°.
Нахождение значений синуса, косинуса и тангенса угла в 45°.
Возьмём прямоугольный треугольник с 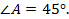 В нём, как в прямоугольном треугольике,
В нём, как в прямоугольном треугольике, 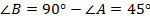 .
. 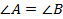 , значит, треугольник равнобедренный,
, значит, треугольник равнобедренный, 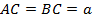 .
.
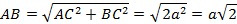
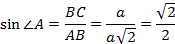
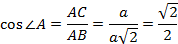
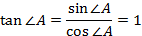
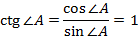
 2015-04-12
2015-04-12 7445
7445
