4.1-4.20. Найти собственные числа и собственные векторы матрицы А.
4.1. А = 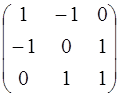 ; 4.2. А =
; 4.2. А = 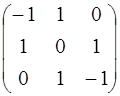 ;
;
4. 3. А = 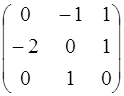 ; 4.4. А =
; 4.4. А = 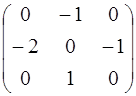 ;
;
4. 5. А = 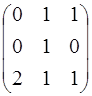 ; 4.6. А =
; 4.6. А = 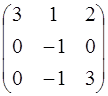 ;
;
4.7. А = 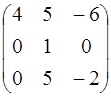 ; 4.8. А =
; 4.8. А = 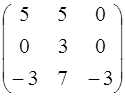 ;
;
4.9. А = 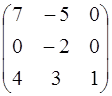 ; 4.10. А =
; 4.10. А = 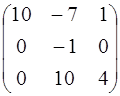 ;
;
4. 11. А = 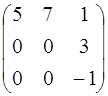 ; 4.12. А =
; 4.12. А = 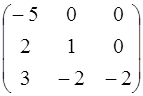 ;
;
4.13. А = 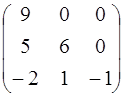 ; 4.14. А =
; 4.14. А = 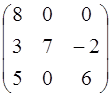 ;
;
4.15. А = 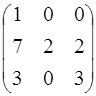 ; 4.16. А =
; 4.16. А = 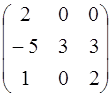 ;
;
4.17. А = 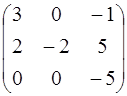 ; 4.18. А =
; 4.18. А = 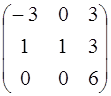 ;
;
4.19. А = 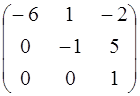 ; 4.20. А =
; 4.20. А = 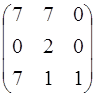 .
.
Указания к задаче 4: с обственные числа и собственные векторы
Число 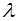 называется собственным числом квадратной матрицы А n -ого порядка, если существует такой ненулевой n -мерный вектор Х, что А Х =
называется собственным числом квадратной матрицы А n -ого порядка, если существует такой ненулевой n -мерный вектор Х, что А Х = 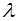 Х.
Х.
Этот ненулевой вектор Х называется собственным вектором матрицы А, соответствующим ее собственному числу 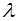 .
.
Множество всех собственных чисел матрицы А совпадает с множеством всех решений уравнения 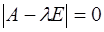 , которое называется характеристическим уравнением матрицы А.
, которое называется характеристическим уравнением матрицы А.
Множество всех собственных векторов матрицы А, соответствующих ее собственному числу 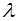 , совпадает с множеством всех ненулевых решений системы однородных уравнений
, совпадает с множеством всех ненулевых решений системы однородных уравнений
(А - 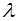 Е) = 0.
Е) = 0.
Задача 4.
Найти собственные числа и собственные векторы матрицы А.
А = 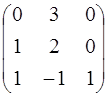 .
.
Решение: Найдем характеристическое уравнение матрицы А – определитель матрицы А - 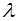 Е, где Е – единичная матрица,
Е, где Е – единичная матрица, 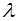 –независимая переменная.
–независимая переменная.
А – 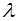 Е =
Е = 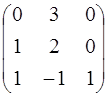 –
– 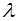
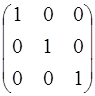 =
= 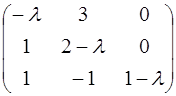 .
.
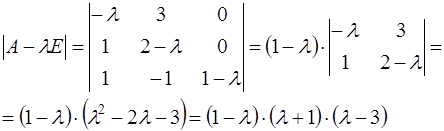
При вычислении данного определителя использовалось его разложение по элементам третьего столбца.
Найдем теперь собственные числа матрицы А – корни характеристического уравнения 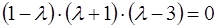 . Получаем:
. Получаем:
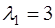 ,
, 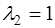 ,
, 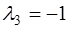 .
.
Далее найдем собственные векторы матрицы А, соответствующие каждому из собственных чисел.
Пусть
Х = 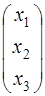 – искомый собственный вектор.
– искомый собственный вектор.
Тогда система однородных уравнений (А - 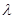 Е) = 0 выглядит так:
Е) = 0 выглядит так:
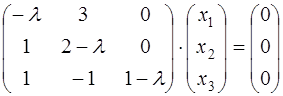
или
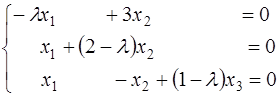 (1)
(1)
Эта однородная система линейных уравнений имеет множество решений, так как ее определитель равен нулю.
При 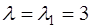 система (1) принимает вид:
система (1) принимает вид:
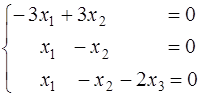
Общее решение этой системы 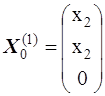 , где
, где 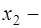 любое число.
любое число.
В качестве собственного вектора достаточно взять любое частное решение. Пусть, например, 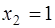 , тогда собственный вектор, соответствующий собственному числу
, тогда собственный вектор, соответствующий собственному числу 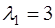 , имеет вид
, имеет вид
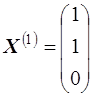 .
.
При 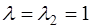 система (1) принимает вид:
система (1) принимает вид:
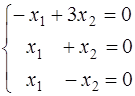
Общее решение этой системы 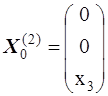 , где
, где 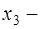 любое число.
любое число.
Пусть, например, 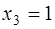 , тогда собственный вектор, соответствующий собственному числу
, тогда собственный вектор, соответствующий собственному числу 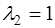 , имеет вид
, имеет вид
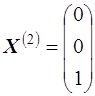 .
.
Аналогично при 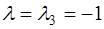 получаем систему
получаем систему
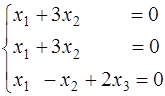 ,
,
общее решение которой 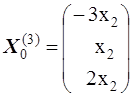 , где
, где 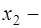 любое число.
любое число.
Пусть 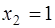 , тогда собственный вектор, соответствующий собственному числу
, тогда собственный вектор, соответствующий собственному числу 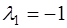 , имеет вид
, имеет вид
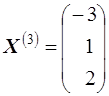 .
.
Ответ: 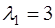 ,
, 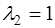 ,
, 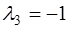 ,
,
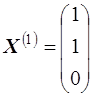 ,
, 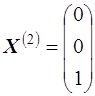 ,
, 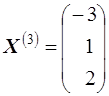 .
.
 2015-04-12
2015-04-12 1565
1565
