Основы теории дискретных случайных величин

基本随机变量的理论

Закон распределения дискретной случайной величины Х имеет форму ряда распределения. Это таблица, связывающая все возможные значения случайной величины и вероятности, с которыми эти значения реализуются.随机变量的分布规律具有分布形式公式。下面表格，包括所有变量的数值与相应概率。

Х			...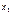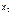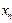
Р			...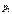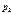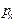

Вероятности реализации событий связаны соотношением所有这些概率合起来是1.

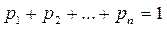(4.1)

Графическое изображение ряда распределения называется полигоном распределения.图像绘制分布排列叫分布轨迹。

4.2. Пример решения типовых заданийпо теме «Ряд распределения дискретной случайной величины» 例题详解

Задание № 4. Вариант 1. Коля, Петя и Сережа готовятся к экзамену по статистике. Коля может получить пятерку с вероятностью 90%, Петя – 70%, а Сережа – 20%. Построить ряд распределения и полигон числа пятерок, которые друзья могут получить на экзамене по статистике.

Коля, Петя и Сережа三人准备统计考试，Коля可以获得5分的概率是90%, Петя 是70%， Сережа是20%。建立统计考试5分的分布规律与图像。

Решение. Прежде всего, определим форму ряда распределения случайной величины Х – числа пятерок, которые трое друзей могут получить на экзамене по статистике. Действительно, на троих они могут не получить ни одной пятерки, получить 1, 2 или 3 пятерки. Значит, ряд распределения в общем виде таков: 首先决定三人获得5分的随机变量分布规律公式，当然三人可能获得不知一个，可能1个，2个，或者3个5分。

Х
Р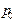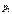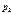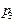

Осталось найти значения вероятностей .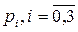

Обозначим вероятности получения пятерки Колей 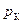= 0,9, Петей 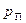= 0,7, Сережей 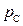= 0,2. Соответственно, вероятность не получить пятерку для Коли 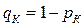= 1 – 0,9 = 0,1, для Пети 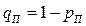= 1 – 0,7 = 0,3, для Сережи 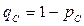= 1 – 0,2 = 0,8.

Тогда вероятность не получить ни одной пятерки для трех друзей будет三人1个5分都没有的概率

.

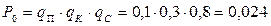Событие «Получить 1 пятерку на троих» означает, что пятерку получит или Коля, или Петя, или Сережа, а остальные двое пятерок не получат. Вероятность этого события三人获得一个5分，意味着其中一人5分，另外两人没有5分，这个概率是

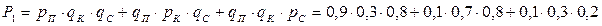
= 0,216 + 0,056 + 0,006 = 0,278.

Аналогично вычисляется вероятность получения двух пятерок на троих

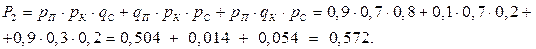
Вероятность получения пятерок всеми 3 друзьями равна

.

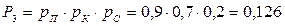Найденные значения вероятностей позволяют завершить составление ряда распределения случайной величины Х, который принимает вид

Х
Р	0,024	0,278	0,572	0,126

Очевидно, что 0,024 + 0,278 + + 0,572 + 0,126 = 1, т.е. выполняется соотношение (4.1) и построенный ряд распределения отвечает требованиям нормировки.

Наиболее вероятным оказалось событие «Получить 2 пятерки на троих». Действительно, исходные значения вероятностей свидетельствуют в пользу того, что Петя и Коля, скорее всего, получат пятерки по статистике, а Сережа – нет. Как правило, результат математических вычислений в теории вероятностей подтверждает соображения житейской логики.

Графический образ построенного ряда распределения – полигон.建立图像。 Для построения полигона по оси Х отложим в выбранном масштабе значения случайной величины: 0, 1, 2 и 3. На оси У найдем в другом масштабе соответствующие этим значениям вероятности: 0,024, 0,278, 0,572 и 0,126. Это будут соответственно абсциссы и ординаты узловых точек полигона. Построим эти узловые точки по заданным координатам. Соединив их отрезками прямых линий, получим требуемый чертеж полигона (рис. 4.1).

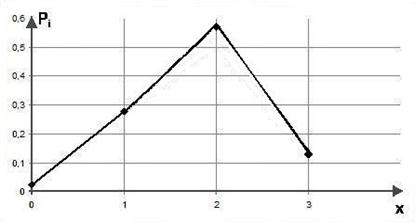
Рис. 4.1.Полигон числа пятерок, полученных друзьями
на экзамене по статистике

Задание № 4. Вариант 2. Компьютерный класс № 1 бывает занят в день 4 или 6 часов в зависимости от четной или нечетной учебной недели. Компьютерный класс № 2 используется для тестирования и бывает занят 3 часа в день в 90% случаев или 5 часов – в 10% случаев. Построить ряд распределения и полигон общего числа часов дневной занятости компьютерных классов. 计算机1号教室可能在单双周每天使用4个课时或者6个课时。计算机2号教室90%的时间每天使用3个课时，或者10%的时间每天使用5个课时。建立计算机教室使用随机变量分布规律和图像。

Решение. Пусть случайная величина Х – число часов в день, когда заняты оба компьютерных класса. Для построения ряда распределения Х сначала составим ряды распределения величин 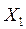и 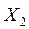- числа часов занятости компьютерных классов № 1 и № 2 по отдельности.设随机变量X为每天两间教室的课时数量，先分别建立不同教师的随机变量分布规律。

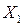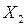Р	0,5	0,5		Р	0,9	0,1

Случайная величина Х может принимать значения, равные возможным суммам значений величин 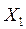и 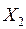. Ряд распределения Х имеет вид

随机变量X可以取不同的课时总数

Х
Р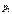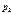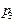

Найдет значения вероятностей 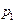, , 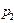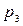. Значение Х = 9 случайная величина принимает, если компьютерный класс № 1 работает 4 часа, а класс № 2 – 5 часов:

.

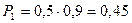Значение Х = 11 случайная величина принимает, если компьютерный класс № 1 работает 4 часа, а класс № 2 – 7 часов или компьютерный класс № 1 работает 6 часов, а класс № 2 – 5 часов:

.

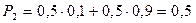Значение Х = 13 случайная величина принимает, если компьютерный класс № 1 работает 6 часов, а класс № 2 – 7 часов:

.

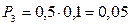Ряд распределения случайной величины Х можно записать в виде

Х
Р	0,45	0,5	0,05

Очевидно, что 0,45 + 0,5 + + 0,05 = 1, и для построенного ряда выполнено соотношение нормировки (4.1)..

Полигон распределения строится аналогично варианту 1 (рис. 4.2).

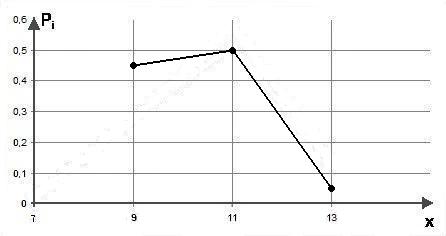
Рис. 4.2.Полигон числа часов дневной загрузки
двух компьютерных классов

4.3. Задания по теме «Ряд распределения дискретной
случайной величины»习题

4.1. Студент Саша получает в сессию 4 пятерки с вероятностью 65% или 2 пятерки с вероятностью 35%, а Маша получает одну или 2 пятерки с равной вероятностью. Построить ряд распределения и полигон числа пятерок у этой парочки.学生Саша在考试中获得4个5分的概率是65%，或者2个5分概率为35%，而学生Маша获得1个或者2个5分是一样的概率。建立不同5分情况的分布规律图像。

4.2. Коля может подтянуться на турнике 8 раз с вероятностью 70% или 9 раз с вероятностью 30%, а Петя 4 или 5 раз с теми же вероятностями. Построить ряд распределения и полигон числа подтягиваний при очередном походе друзей в спортзал.Коля做单杠引体向上，做8次的概率是70%，或者30%的概率做9次。而Петя同样的概率分别做4次和5次。建立不同次数情况的分布规律图像。

4.3. В студенческой группе 9 россиян и 2 иностранца, все учатся одинаково успешно. В магистратуре по этому направлению подготовки 3 места. Построить ряд распределения и полигон числа россиян, продолживших обучение в магистратуре при случайном отборе кандидатов.在班级中有9名俄罗斯学生和2名外国学生，全部都顺利结业。这个专业硕士有3个名额。建立在随机挑选的条件下，俄罗斯学生继续硕士学习的分布规律图像。	4.4. Из 9 американских студентов, прибывших в Санкт-Петербург в летнюю школу, 6 плохо перенесли перелет. В группе студентов, владеющих русским языком на нулевом уровне 4 человека. Построить ряд распределения и полигон числа студентов, плохо перенесших перелет из группы нулевого уровня.9名来自美国到圣彼得堡参加暑期短讯的学生中，有6名不适应飞行。在其中有4名从零开始学习。建立从零开始学习并且不适应飞行的学生的分布规律图像。
4.5. При заходе в магазин Оля покупает крем с вероятностью 70%, а Поля – с вероятностью 30%. Построить ряд распределения и полигон числа приобретенных тюбиков крема при очередном набеге подруг на магазин.到商店后Оля购买面霜的概率是70%，Поля是30%，建立在商店两人先后购买面霜的分布规律图像。	4.6. Маша роняет вазу с вероятностью 30%, а ее сестра Поля – с вероятностью 45%. Построить ряд распределения и полигон числа разбитых ваз, если при приходе гостей с 2 букетами обе сестры бросились помогать поставить цветы.Маша打碎花瓶的概率是30%，Поля打碎花瓶的概率是45%。如果客人带来2束鲜花，建立两位姐妹插花时打碎花瓶的分布规律图像。
4.7. Из 11 одинаковых учебников в фонде библиотеки 6 испорчены рисунками. Новым студентам выдано 3 учебника. Построить ряд распределения и полигон числа не разрисованных учебников, выданных студентам.在图书馆的11本相同的教科书中有6本的插图破损。给新生借出3本，建立新生拿到插图破损的教科书的分布规律图像。	4.8. У Антона 3 задолженности, а у Толика 5. Антон может сдать задолженность с вероятностью 40%, а Толик – 60%. Построить ряд распределения и полигон числа задолженностей, оставшихся у друзей после пересдачи.安东有3门科目没有通过考试，多林卡有5门。安东通过考试的概率是40%，多林卡是60%。建立补考后两人没有通过的科目的分布规律图像。

4.09. У Жанны 15 попугаев – 8 зеленых и 5 желтых. 3 попугая улетели. Построить ряд распределения и полигон числа желтых попугаев среди улетевших.让那有15只鹦鹉，其中8只绿色和5只黄色。飞走了3只。建立夫走三只中有黄色鹦鹉的分布规律图像。

4.10.В столовой из 9 порций салата 5 с недовесом. Для контроля выбрали 4 порции. Построить ряд распределения и полигон числа порций с недовесом среди взятых для контроля.在食堂有9分分量不足的沙拉，选了4分进行抽查。建立抽查选到分量不足沙拉的分布规律图像。

5. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

随机变量的数字特征

5.1. Основы теории числовых характеристик дискретной случайной величины 随机变量数字特征基本理论

Ряд распределения дискретной случайной величины (ДСВ) Х имеет вид:随机变量X（ДСВ）的分布

Х			...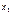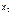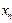
Р			...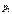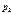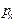

Вероятности реализации событий связаны соотношением (4.1):

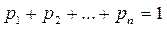. (5.1)

Математическое ожидание ДСВ вычисляется по формуле

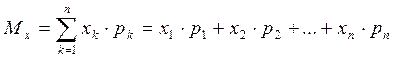. (5.2)

Дисперсия ДСВ вычисляется по формуле

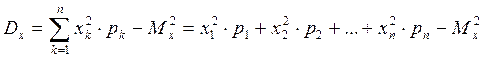. (5.3)

Средне квадратическое отклонение (или просто отклонение) ДСВ вычисляется по формуле

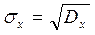. (5.4)

Вероятность попадания ДСВ на участок равна сумме вероятностей, с которыми реализуются значения случайной величины, попадающие на этот участок.Такое вычисление вероятности возможно произвести, поскольку все значения, которые принимает случайная величина, попарно несовместны.

Модой называется наиболее вероятное значение случайной величины.

Значения функции распределения ДСВ Х находятся согласно следующему правилу

,

,

,

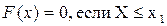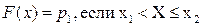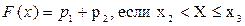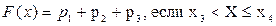, (5.5)

. .............................

,

.

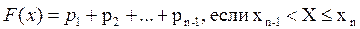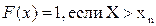Можно построить таблицу значений функции распределения, имеющей постоянные значения на интервалах:

Х			...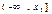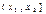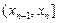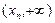
F(x)			...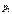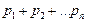

Графиком функции распределения, очевидно, является неубывающая ступенчатая функция, поскольку, согласно определению, все значения вероятности неотрицательны, а значит в нижнем ряду рассматриваемой таблицы суммируются с нарастанием неотрицательные величины. Такая функция иногда называется кусочно-постоянной.Ее вид можно посмотреть ниже для конкретных данных примера № 5 (рис. 5.2).

5.2. Пример решения типового задания по теме
«Числовые характеристики дискретной случайной величины»

Задание № 5. Дан ряд распределения дискретной случайной величины. 给出随机变量分布规律

Х
Р	a	0.5	0.3	0.1

Найти求出a, M_x,D_x,σ_х, Р (40<Х<50), Р (Х>35), Р (Х<150). Построить полигон, указать моду. Построить функцию распределения. 建立分布图像和函数分布。

Решение. Установим, что число значений ДСВ n = 4. Используя соотношение (5.1), получаем

.

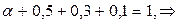
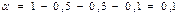Математическое ожидание находим по формуле（5.2），数学期望根据公式（5.2）可以求出

.

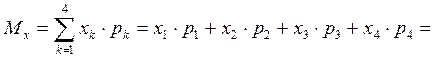
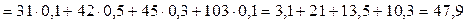Дисперсию находим по формуле (5.3)

.

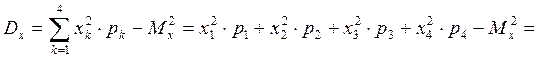
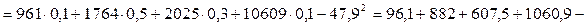
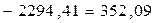Средне квадратическое отклонение находим по формуле (5.4)

.

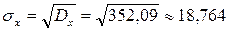Такая величина отклонения, особенно при сопоставлении с математическим ожиданием на первый взгляд свидетельствует об определенном разбросе значений ДСВ, их недостаточной сгруппированности для того, чтобы в точных вероятностных моделях явлений, описываемых такой ДСВ, заменять эту величину ее средним по вероятности значением. Однако, с другой стороны, если рассмотреть оценку 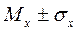, то можно заметить, что в интервал

.

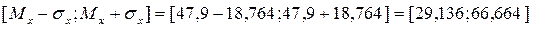попадает 3 из 4 значений случайной величины, т.е. 75% ее значений, а это значит, что в приближенных вероятностных моделях вполне допустимо пользоваться математическим ожиданием данной ДСВ в качестве ее среднего значения, определяющего место ДСВ на числовой оси.

Для построения полигона, как и в разделе 4, по оси Х отложим в выбранном масштабе значения случайной величины: 31, 42, 45 и 103. На оси У найдем в другом масштабе соответствующие этим значениям вероятности: 0,1, 0,5, 0,3 и 0,1. Это будут соответственно абсциссы и ординаты узловых точек полигона. Построим эти узловые точки по заданным координатам. Соединив узловые точки отрезками прямых линий, получим требуемый чертеж полигона (рис. 5.1).

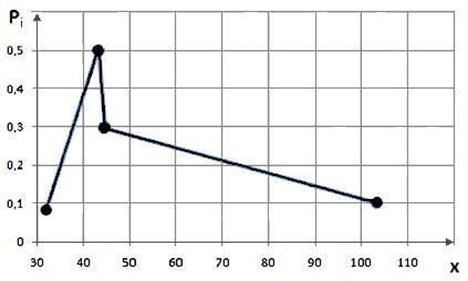
Рис. 5.1.Полигонраспределения ДСВ

Из рис. 5.1 видно, что наиболее вероятное значение ДСВ Х = 45, оно и будет модой распределения, т.е. mod = 45.Распределение является унимодальным, т.е. имеющим одну моду, причем ярко выраженную. Что, в свою очередь, подтверждает вывод: несмотря на относительно большой разброс, значения ДСВ достаточно сгруппированы относительного среднего – математического ожидания. Таким образом, математическое ожидание дает адекватное представление о месте рассматриваемой ДСВ на числовой оси. Действительно, 3 значения ДСВ – 31, 42 и 45 – сгруппированы вокруг математического ожидания 47,9. Единственное значение 103, разительно отличающееся и от остальных значений и от математического ожидания, ДСВ принимает с небольшой вероятностью 10%.

Найдем вероятности попадания ДСВ на заданные участки.

Р (40<Х<50) = Р(Х = 42) + Р(Х = 45) = 0,5 + 0,3 = 0,8,

Р (Х>35) = Р(Х = 42) + Р(Х = 45) + Р(Х = 103) = 0,5 + 0,3 + 0,1 = 0,9,

Р (Х<150) = Р(Х = 31) + Р(Х = 42) + Р(Х = 45) + Р(Х = 103) =

= 0,1 + 0,5 + 0,3 + 0,1 = 1.

Видно, что вероятность попадания ДСВ в сравнительно узкий интервал от 40 до 50 составляет 80%, что в очередной раз подтверждает факт сгруппированности значений ДСВ вокруг математического ожидания, которое со значением 47,9 попадает на тот же самый интервал.

Функцию распределения ДСВ строим, используя правило (5.5):

,

,

,

.

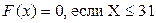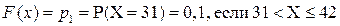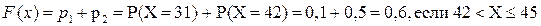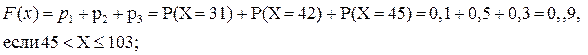
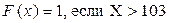Таблица значений функции распределения имеет вид

Х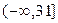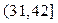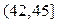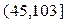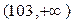
F(x)		0,1	0,6	0,9

График этой ступенчатой функций изображен на рис. 5.2. Причем по обеим осям координат выбран подходящий масштаб, который обычно бывает различным, т.е. наиболее удобным и наглядным для каждой оси.

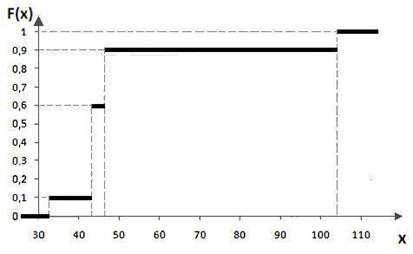
Рис. 5.2. Функция распределенияДСВ

5.3. Задания по теме «Числовые характеристики
дискретной случайной величины»习题

Текст задания. Дан ряд распределения дискретной случайной величины. Найти a, M_x,D_x,σ_х, Р (a <Х< b), Р (Х> c), Р (Х< d).

Построить полигон, указать моду. Построить функцию распределения.

Таблица 5.1

Варианты задания

5.1. a = 30, b = 120, c = 60, d = 850.	5.2. a = 10, b = 50, c = 30, d = 60.
a	0.1	0.1	0.1	0.1	0.1	a	0.2	0.1	0.1	0.1
5.3. a = 0, b = 20, c = 35, d =870.	5.4. a = 10, b = 30, c = 20, d = 30.
0.1	0.2	a	0.1	0.1	0.1	0.1	a	0.3	0.2	0.1
5.5. a = 30, b = 90, c = 60, d = 200.	5.6. a = 30, b = 70, c = 40, d = 20.
0.2	a	0.2	0.1	0.1	0.1	0.2	a	0.2	0.1	0.1
5.7. a = 10, b = 60, c = 100, d = 90.	5.8. a = 10, b = 15, c = 40, d = 160.
0.1	0.1	0.2	a	0.2	0.1	0.1	0.1	a	0.1	0.1
5.9. a = 10, b = 200, c = 130, d = 10.	5.10. a = 90, b = 100, c = 140, d = 170.
0.2	0.3	a	0.1	0.1	0.1	0.1	0.1	a	0.2	0.2