Используются понятия теории вероятности, которые были сформулированы в 30 годах 20 века академиком Андреем Николаевичем Колмогоровым.
Функция, значение которой при каждом значении независимой переменной является случайной величиной, называется случайной функцией.
Случайные функции, для которых независимой переменной является время t, называются случайными или стохастическими процессами. В процессе X(t) любого вида функция характеризуется тем, что в любой момент времени t ее значения являются случайными величинами. В системах измеряющих информацию процессы протекают во времени. Сигналы являются физическими процессами, протекающими во времени. Поэтому мы будем изучать только случайные процессы X(t).
Случайные процессы X(t) не характеризуются определенной кривой, они характеризуются множеством кривых Xi(t), где I=1, 2,…,n, получаемых в результате отдельных опытов. Каждую кривую этого множества называют реализацией случайного процесса. Сказать заранее, по какой из реализаций пойдет процесс, невозможно. Случайный процесс- бесконечная совокупность реализаций, которая образует статистический сигнал.
Рассмотрим, например, случайный дрейф на выходе усилителя постоянного тока при Uвх=0. Что бы изучить характеристики дрейфа, можно взять n-усилителей при одинаковых условиях работы, поместить их в одинаковые условия работы, и получит n-осциллограмм. Сигналы с выхода усилителей являются ансамблем.
Статистические методы изучают не каждую из реализаций Xi(t) из множества X(t), а свойства всего множества в целом при помощи усреднения свойств входящих в него реализаций. Поэтому при исследовании различных систем судят о их поведении не по отношению к какому-либо определенному воздействию, представляющему заданную функцию времени, а по отношению к целой совокупности воздействий.
Задать диапазон случайной величины- указать все возможные ее значения и поставить в соответствие вероятности, с которыми случайная величина (СВ) принимает эти значения.
Статистические свойства непрерывной случайной величины X определяют по ее функциираспределения вероятности F(X) (интегральный закон распределения) или плотности вероятности f(X) (дифференциальный закон распределения) 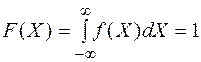 . Случайная величина может иметь равномерный, нормальный, экспоненциальный или другие законы распределения.
. Случайная величина может иметь равномерный, нормальный, экспоненциальный или другие законы распределения.
Чтобы охарактеризовать Д.С.В.(дискретная случайная величина)- необходимо знать все возможные значения, которые она может принимать и вероятности появления каждого из этих значений.

 P
P

 X1, X2,…, Xn P1 P2 Pn F
X1, X2,…, Xn P1 P2 Pn F









 P1, P2,…, Pn …
P1, P2,…, Pn …




 X X
X X
Н.С.В.(непрерывная случайная величина)- может принимать значения в к-л заданном ограничивающим интервалом (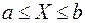 ) или (-¥, ¥).
) или (-¥, ¥).
Законы распределения С.В.
1)биномиальный;
2)Пуассона;
3)Закон равной вероятности;
4)нормальное распределение (Гаусса);
5)экспоненциальный;
6)Вейбула-Гнеденко;
7)Симпсона;
8)Рэлея;
9)x- распределение;
10)усеченные логарифмические
Закон равной вероятности
С.В. X Ñ называется распределенной по закону равной вероятности (равномерной з.р.), если 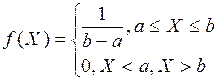
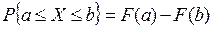
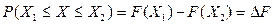
f(X)





 1
1

 P
P




 Х
Х

 f(x) a в
f(x) a в 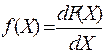



 1/(в-а)
1/(в-а)




 X
X
a в
X1 X2
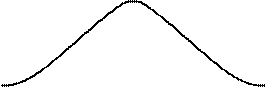
Нормальное распределение - С.В. Х Ñ называется распределенной по нормальному закону, если плотность вероятности 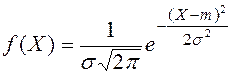 , где m, s- параметры распределения вероятности
, где m, s- параметры распределения вероятности 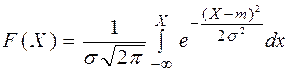 (*) или
(*) или 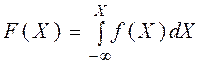 . Интеграл (*) по любым пределам не берется, для этого используются таблицы.
. Интеграл (*) по любым пределам не берется, для этого используются таблицы.
Нормальное распределение.



 F(X) f(X) s1<s2
F(X) f(X) s1<s2




 1 s1
1 s1



 s
s 1 s2 0,607 fmax
1 s2 0,607 fmax


 s2
s2














 s1<s2 s s s 0 X X = m X= m
s1<s2 s s s 0 X X = m X= m

 3s 3s
3s 3s
Кривая f(X) для С.В., распределенной по нормальному закону, симметрична относительно точки X= m. Эта точка является центром распределения. Чем больше s, тем положе кривая f(X).
X= m- центр, около которого группируются возможные значения С.В. Х.
s- мера величины рассеяния С.В. около m.
Функция распределения вероятностей F(X) и плотность распределения вероятностей f(X)
Функция распределения (Ф.Р.)- это вероятность того, что случайная величина X примет значение £ некоторого уровня X.
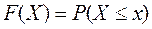 .
.
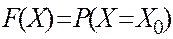 - очень мала.
- очень мала.
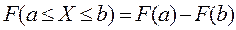 - конечная величина.
- конечная величина.
F(X)- гладкая неубывающая функция, 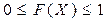 .
.
 F(-¥)=0; F(+¥)=1 F(X) дискретная С.В.
F(-¥)=0; F(+¥)=1 F(X) дискретная С.В.














 F(X) X
F(X) X

 1 X1 X2 X3
1 X1 X2 X3

s1 s2
непрерывная
 величина
величина
0 X = m X
Для нормального закона распределения 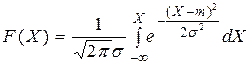 .
.
Вероятность 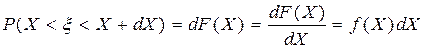 .
.
Производная от F(X)- плотность распределения вероятностей Х
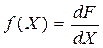
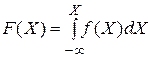 ,
,
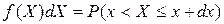 .
. 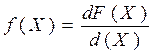 .
.
Для непрерывной случайной величины f(X)- гладкая функция, для дискретной С.В.- 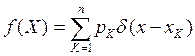 ступенчатая (негладкая).
ступенчатая (негладкая).
Свойства f(x)
1)f(x)-неотрицательная величина f(x)³0.
2)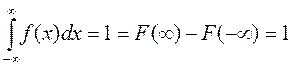
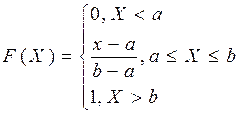 .
.
σX – среднее квадратическое отклонение.
Функция распределения 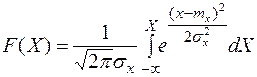
Плотность вероятности 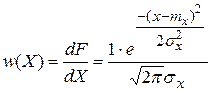
Сигнал – это вектор, вектор многомерная с.в., координаты вектора - одномерн. с. в.
Для случайного процесса X(t) также вводят понятие функции распределения F(X,t) и плотности распределения вероятности f(X,t), которые зависят от фиксированного момента времени t1 и от некоторого выбранного уровня X.
Одномерной функцией распределения называют вероятность того, что значение случайного процесса X(t) в момент времени t1 не превышает некоторого заданного уровня(числа) X1, т. е.
F1(X1,t1)=P{X(t1)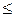 X1}
X1}
и одномерная плотность вероятности
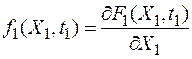
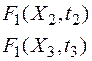
Одномерная Ф.Р. F1(X1,t1) и П.Р.В. f1(X1,t1) не позволяет судить о характере развития реализации случ. процесса во времени. Больше сведений получим, если иметь 2 сечения сл. процесса в несовпад. t1 и t2.
Возникает двумерная функция распределения:
Рассмотрим случайные величины X(t1) и X(t2),относящиеся к двум разным моментам времени t1 и t2 наблюдения случайного процесса X(t). Вероятность того, что X(t1) будет не больше X1 при t= t1 и не больше X2 при t= t2, т.е. 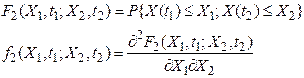 .
.
Двумерная плотность вероятности или плотность вероятности второго порядка.
Величина 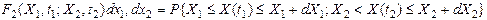 равна вероятности того, что X(t) при t=t1 будет находиться в интервале
равна вероятности того, что X(t) при t=t1 будет находиться в интервале 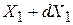 ,
,
А при t= t2 будет находиться в интервале 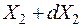 . Также вводятся F3,…,Fn, f3,…,fn, многомерные ф.р. и пл.в. при n-мерном (n>2) сечении случ. проц.
. Также вводятся F3,…,Fn, f3,…,fn, многомерные ф.р. и пл.в. при n-мерном (n>2) сечении случ. проц.
Свойства F2 – те же 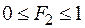 .
.
Понятие функции распределения и плотности вероятности полностью характеризуют случайный процесс. Однако определение их представляет значительные трудности на практике и они не используются.
На практике используются более простые, хотя и менее полные характеристики случайных процессов: математическое ожидание, дисперсия, среднее значенье квадрата случайного процесса, корреляционная функция, спектральная плотность.
Математическим ожиданием (средним значением)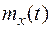 случайного процесса
случайного процесса 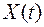 называют величину
называют величину 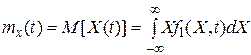
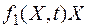 - элементарная вероятность
- элементарная вероятность
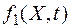 - одномерная плотность вероятности случайного процесса.
- одномерная плотность вероятности случайного процесса.
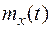 - теоретич. оценка ср. знач. случ. процесса
- теоретич. оценка ср. знач. случ. процесса
для дискретной С.В.
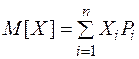
Xi – возможные значения X
Pi – вероятность того, что С.В. примет значение Xi.
Это не случайная функция времени 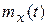 , около которой группируются и относительно которой колеблются все реализации данного случайного процесса.
, около которой группируются и относительно которой колеблются все реализации данного случайного процесса.



 X(t)
X(t)
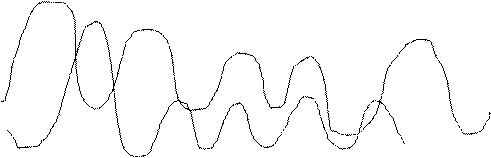 |
 w2
w2
 w1
w1
t1 t2 …… tK
| |||
| |||




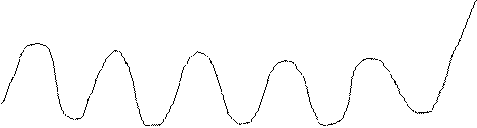
 mX(t)
mX(t)
 |
X(t) X(t)
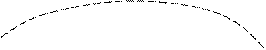





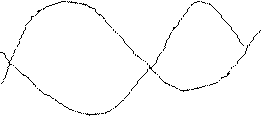
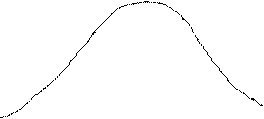 mX+3s
mX+3s
 | |||
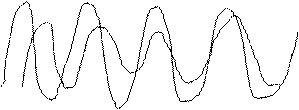 | |||

 mX
mX
 | |||
 |
a) t1 t2 mX-3s б) t1 t2
Реализации 2-х сл. проц. X(t) с одним. М.О. и Д., но в
а) –С.П. изм-ся быстрее, связь между сечением t1 и t2 мала
б) –С.П. изм-ся медленнее, зав-ть между сечениями больше
Свойства М.О.
1)М.О. М[C]=C неслуч. вектора=самому этому вектору
2) Неслучайный множитель С можно выносить за знак М.О.
M[CX]=CM[X]
C - неслуч. в-на
C – неслуч. матрица
3) 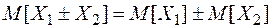
Вводят иногда в рассмотрение центрированный случайный процесс 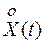 , который определяется как отклонение случайного процесса X(t) от среднего значения
, который определяется как отклонение случайного процесса X(t) от среднего значения 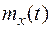

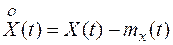
Тогда X(t) равна сумме двух составляющих: регулярной составляющей=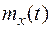
и центрированной случайной составляющей 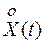 , т.е.
, т.е.

Очевидно М.О. центр. составляющей
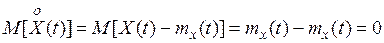


Средним значением квадрата случайного процесса называют величину
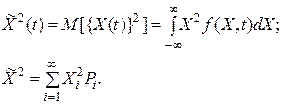
 Чтобы учесть степень разбросанности реализаций случайного процесса относительно его среднего значения, вводят понятие дисперсии случайного процесса, числовая характеристика которая равна математическому ожиданию квадрата центрированного случайного процесса. D характеризует отклонение значений, принимаемых X(t), от М.О. Чем больше разброс возможных значений С.В. от М.О., тем больше дисперсия
Чтобы учесть степень разбросанности реализаций случайного процесса относительно его среднего значения, вводят понятие дисперсии случайного процесса, числовая характеристика которая равна математическому ожиданию квадрата центрированного случайного процесса. D характеризует отклонение значений, принимаемых X(t), от М.О. Чем больше разброс возможных значений С.В. от М.О., тем больше дисперсия

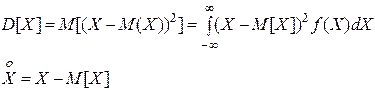
Свойства дисперсии
1) D[C]=0 C – неслучайная величина
D[C]=M[(C-M[C])]=M[(C-C)2]=0
2) D[CX]=C2D[X]
3) D[X1+X2]=D[X1]+D[X2]
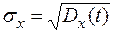
 - Ñ- среднее арифметическое отклонение;
- Ñ- среднее арифметическое отклонение;
мера разброса результатов отдельных случ. испытаний относительно М.О.
Можно сказать, что математическое ожидание 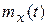 , дисперсия
, дисперсия 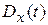 и среднее значение квадрата
и среднее значение квадрата 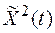 случайного процесса, имеющие размерность квадрата случайной величины, связаны соотношением.
случайного процесса, имеющие размерность квадрата случайной величины, связаны соотношением.
Доказательство: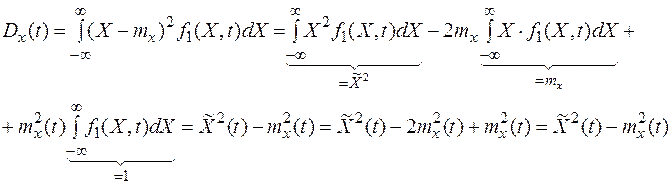
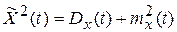

Отсюда видно, что среднее значение квадрата случайного процесса 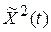 в определенной мере учитывает и среднее значение случайного процесса, и степень рассеяния его реализаций относительно этого среднего значения, поэтому широко используется в качестве оценки точности системы автоматического управления.
в определенной мере учитывает и среднее значение случайного процесса, и степень рассеяния его реализаций относительно этого среднего значения, поэтому широко используется в качестве оценки точности системы автоматического управления.
На практике удобно пользоваться статистическими характеристиками случайного процесса, имеющими ту же размерность, что и сама случайная величина. К ним относятся:
- среднее квадратическое значение случайного процесса (СК)
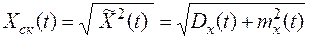
равное арифметическому значению квадратного корня из среднего значения квадрата случайного процесса;
- среднее квадратическое отклонение случайного процесса (СКО)
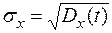
равное арифметическому значению квадратного корня из дисперсии случайного процесса.
M и D – достаточно для решения многих задач.
Лекция № 10
 2014-01-31
2014-01-31 1153
1153
