2015-04-01
1144
Закон Ампера (сила, действующая на проводник с током в магнитном поле)
, 
,
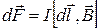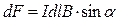где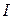 
– сила тока в проводнике, 
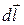– элемент проводника, 
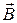– магнитная индукция поля, 
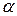– угол между векторам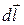и и 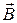. В однородном магнитном поле (
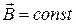) сила Ампера, действующая на прямолинейный проводник длиной 
,
.
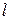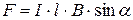Максимальная сила при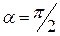 
.
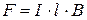Связь магнитной индукции 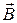с напряженностью 
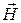магнитного поля
,
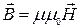где μ – магнитная проницаемость изотропной среды; μ0 – магнитная постоянная.
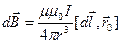или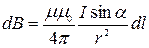 
,
где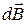 
– магнитная индукция поля, создаваемого элементом провода длиной 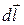с током I; 
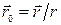– единичный вектор радиус-вектора 
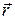, направленный от элемента проводника к точке, в которой определяется магнитная индукция; α – угол между направлением элемента провода 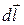и радиус-вектором .
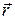Магнитная индукция в центре кругового тока
,
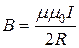где R – радиус кругового витка.
Магнитная индукция на оси кругового тока
,
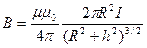где h – расстояние от центра витка до точки, в которой определяется магнитная индукция.
Магнитная индукция поля прямого тока
,
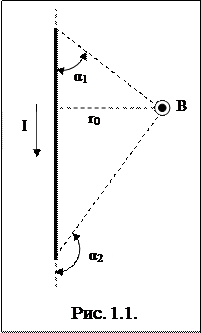
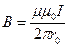где r0 – расстояние от оси провода до точки, в которой определяется магнитная индукция.
Магнитная индукция поля, создаваемого отрезком провода с током (рис. 1.1),
.
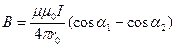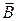Обозначения ясны из рисунка. Направление вектора магнитной индукции обозначено точкой – это значит, что В направлен перпендикулярно плоскости чертежа к нам.
При симметричном расположении концов провода относительно точки, в которой определяется магнитная индукция, –cos α2 = cos α1 = cos α, тогда
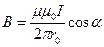
Магнитная индукция поля соленоида
В = μμ0nI,
где n – отношение числа витков соленоида к его длине.
Магнитный момент плоского контура с током
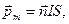
где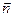 
– единичный вектор нормали (положительной) к плоскости контура; I – сила тока, протекающего по контуру; S – площадь контура.
Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле,
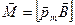или М = pmB sin α,
где α – угол между векторам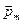и 
и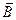 
.
Сила Лоренца
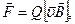или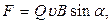 
где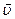 
– скорость заряженной частицы; 
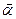– угол между векторам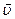и и .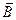
Если частица находится одновременно в электрическом и магнитном полях, то под силой Лоренца понимают выражение
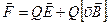
Магнитный поток:
а) в случае однородного магнитного поля и плоской поверхности
Ф = BS cos α или Ф = BnS,
где S – площадь контура; α – угол между нормалью к плоскости контура и вектором магнитной индукции:
б) в случае неоднородного поля и произвольной поверхности
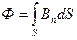
(интегрирование ведется по всей поверхности).
Потокосцепление (полный поток)
Ψ = NФ.
Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.
Работа по перемещению замкнутого контура в магнитном поле
А = I Δ Ф.
ЭДС индукции
.
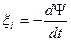Разность потенциалов на концах провода, движущегося со скоростью u в магнитном поле,
U = Blu sin α,
где l – длина провода; α – угол между векторам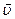и и .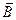
Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур,
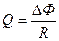, или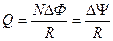 
,
где R – сопротивление контура.
Индуктивность контура
.
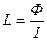ЭДС самоиндукции
.
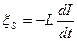Индуктивность соленоида
L = μμ0n2V,
где n – отношение числа витков соленоида к его длине; V – объем соленоида.
Период электромагнитных колебаний в контуре, состоящем из емкости С, индуктивности L и сопротивления R
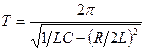
Если мало сопротивление R, то период колебаний определяется формулой Томсона
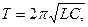
где L – индуктивность; C – электроемкость.
Если R не равно нулю, то колебания будут затухающими, и напряжение на емкости будет меняться по закону
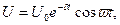
здесь δ = R /2 L – коэффициент затухания; χ = δ T – логарифмический коэффициент затухания.
Если δ = 0, то колебания будут незатухающими
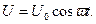
Закон Ома для переменного тока
I эф = U эф/ Z
где I эф и U эф – эффективные значения тока и напряжения связанные с их амплитудными значениями I 0 и U 0
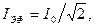
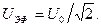
Полное сопротивление цепи переменного тока
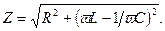
При этом сдвиг фаз между напряжением и током определяется по формуле
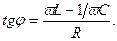
Мощность переменного тока
P = I ЭФ U ЭФ cosφ
Связь между длиной и частотой электромагнитной волны
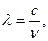
где λ - длина волны; ν - частота колебаний; c – скорость света в вакууме.
