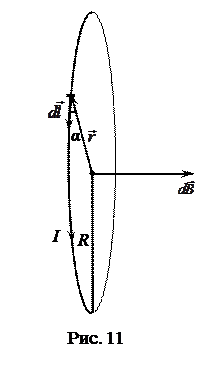
Для нахождения индукции магнитного поля в центре кругового проводника с током необходимо разбить этот проводник на элементы 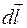 , для каждого из них найти вектор
, для каждого из них найти вектор 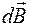 , а затем все эти векторы сложить. Так как все векторы
, а затем все эти векторы сложить. Так как все векторы 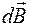 направлены вдоль нормали к плоскости витка (рис. 11), то сложение векторов
направлены вдоль нормали к плоскости витка (рис. 11), то сложение векторов 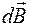 можно заменить сложением их модулей dB.
можно заменить сложением их модулей dB.
По закону Био-Савара-Лапласа модуль вектора 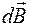 :
:
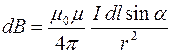 .
.
Так как все элементы 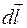 проводника перпендикулярны соответствующим радиусам-векторам
проводника перпендикулярны соответствующим радиусам-векторам 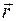 , то sin a = 1 для всех элементов
, то sin a = 1 для всех элементов 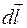 . Расстояния r = R для всех элементов проводника
. Расстояния r = R для всех элементов проводника 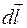 . Тогда выражение для модуля вектора
. Тогда выражение для модуля вектора 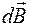 :
:
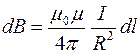 .
.
Теперь можно перейти к интегрированию:
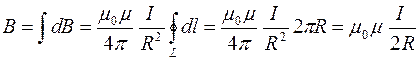 .
.
Итак, индукция магнитного поля в центре кругового проводника с током:
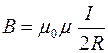 (R – радиус витка с током I).
(R – радиус витка с током I).
Действие магнитного поля на проводник с током (закон Ампера) и на движущийся заряд (сила Лоренца)
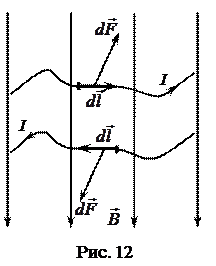
Закон Ампера. На элемент проводника 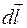 с током I, помещённый в магнитное поле с индукцией
с током I, помещённый в магнитное поле с индукцией  (рис. 12), действует сила
(рис. 12), действует сила 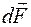 (
(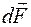 – сила Ампера):
– сила Ампера):
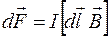 .
.
Модуль вектора 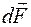 :
: 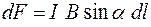 ,
,
где 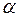 – угол между векторами
– угол между векторами 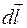 и
и  .
.
|
|
|
Направление вектора 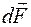 можно определить по правилу левой руки: если силовые линии входят в ладонь, а четыре вытянутых пальца располагаются по току, то отведённый большой палец укажет направление вектора силы Ампера
можно определить по правилу левой руки: если силовые линии входят в ладонь, а четыре вытянутых пальца располагаются по току, то отведённый большой палец укажет направление вектора силы Ампера 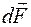 .
.
(Сила 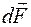 перпендикулярна плоскости рисунка 12.)
перпендикулярна плоскости рисунка 12.)
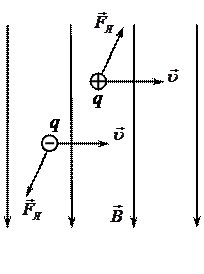
Сила Лоренца. На заряд q, движущийся со скоростью 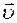 в магнитном поле с индукцией
в магнитном поле с индукцией  (рис. 13), действует сила
(рис. 13), действует сила 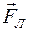 (
(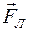 – сила Лоренца):
– сила Лоренца):
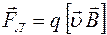 .
.
Модуль вектора 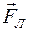 :
: 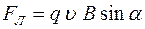 ,
,
где α – угол между векторами 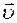 и
и  .
.
Направление вектора 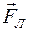 может быть определено по правилу левой руки для движущихся положительных зарядов и по правилу правой руки для движущихся отрицательных зарядов:
может быть определено по правилу левой руки для движущихся положительных зарядов и по правилу правой руки для движущихся отрицательных зарядов:
если силовые линии магнитного поля входят в ладонь, а четыре вытянутых пальца располагаются по скорости движения частицы, то отведённый большой палец укажет направление силы Лоренца (рис. 13, сила 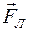 перпендикулярна плоскости рисунка).
перпендикулярна плоскости рисунка).
Магнитный поток. Теорема Гаусса для магнитного поля
Поток вектора магнитной индукции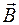 (или магнитный поток) через произвольную площадку S характеризуется числом силовых линий магнитного поля, пронизывающих данную площадку S.
(или магнитный поток) через произвольную площадку S характеризуется числом силовых линий магнитного поля, пронизывающих данную площадку S.
Если площадка S расположенаперпендикулярно силовым линиям магнитного поля (рис. 14), то поток ФB вектора индукции через данную площадку S:
через данную площадку S:
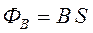 .
.
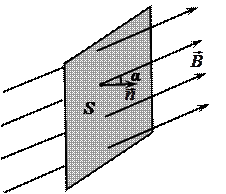

Рис. 14 Рис. 15
Если площадка S расположена неперпендикулярно силовым линиям магнитного поля (рис. 15), то поток ФB вектора индукции  через данную площадку S:
через данную площадку S:
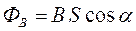 ,
,
где α – угол между векторами  и нормали
и нормали 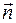 к площадке S.
к площадке S.
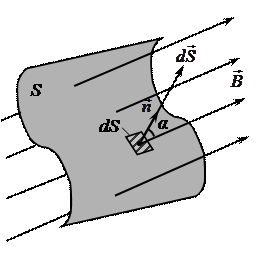
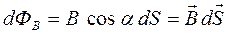 ,Для того, чтобы найти поток ФB вектора магнитной индукции
,Для того, чтобы найти поток ФB вектора магнитной индукции через произвольную поверхность S, необходиморазбить эту поверхность на элементарные площадки dS (рис. 16)иопределить элементарный поток
через произвольную поверхность S, необходиморазбить эту поверхность на элементарные площадки dS (рис. 16)иопределить элементарный поток 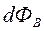 вектора
вектора  через каждую площадку dS по формуле:
через каждую площадку dS по формуле:
|
|
|
где α – угол между векторами  и нормали
и нормали 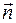 к данной площадке dS;
к данной площадке dS;
Тогда поток вектора  через произвольную поверхность S равен алгебраической сумме элементарных потоков
через произвольную поверхность S равен алгебраической сумме элементарных потоков 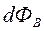 через все элементарные площадки dS, на которые разбита поверхность S, что приводит к интегрированию:
через все элементарные площадки dS, на которые разбита поверхность S, что приводит к интегрированию:
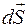 – вектор, равный по величине площади площадки dS и направленный по вектору нормали
– вектор, равный по величине площади площадки dS и направленный по вектору нормали 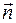 к данной площадке dS.
к данной площадке dS.
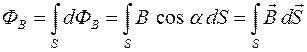 .
.
Теорема Гаусса для магнитного поля
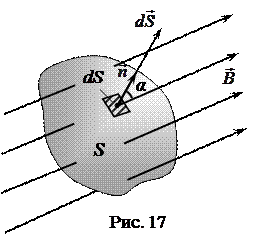
Для произвольной замкнутой поверхности S (рис. 17) поток вектора индукции  магнитного поля через эту поверхность S можно рассчитать по формуле:
магнитного поля через эту поверхность S можно рассчитать по формуле:
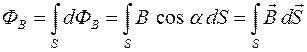 .
.
С другой стороны, число линий магнитной индукции, входящих внутрь объема, ограниченного этой замкнутой поверхностью, равно числу линий, выходящих из этого объема (рис. 17). Поэтому, с учетом того, что поток вектора индукции  магнитного поля считается положительным, если силовые линии выходят из поверхности S, и отрицательным для линий, входящих в поверхность S, суммарный поток ФB вектора
магнитного поля считается положительным, если силовые линии выходят из поверхности S, и отрицательным для линий, входящих в поверхность S, суммарный поток ФB вектора  через произвольную замкнутую поверхность S равен нулю, т.е.:
через произвольную замкнутую поверхность S равен нулю, т.е.:
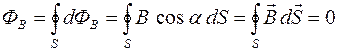 ,
,
что составляет формулировку теоремы Гаусса для магнитного поля.
Явление электромагнитной индукции. Закон Фарадея
Явление возникновения электрического тока в замкнутом проводящем контуре в результате изменения магнитного потока, пронизывающего этот контур, называется явлением электромагнитной индукции. Возникновение индукционного электрического тока в контуре указывает на наличие в этом контуре электродвижущей силы, называемой электродвижущей силой (ЭДС) электромагнитной индукции.
Согласно закону Фарадея величина ЭДС электромагнитной индукции 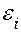 определяется только скоростью изменения магнитного потока, пронизывающего проводящий контур, а именно:
определяется только скоростью изменения магнитного потока, пронизывающего проводящий контур, а именно:
величина ЭДС электромагнитной индукции 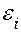 прямо пропорциональна скорости изменения магнитного потока, пронизывающего проводящий контур:
прямо пропорциональна скорости изменения магнитного потока, пронизывающего проводящий контур:
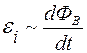 (закон Фарадея).
(закон Фарадея).
Направление индукционного тока в контуре определяется по правилу Ленца: индукционный ток в контуре всегда имеет такое направление, что создаваемое этим током магнитное поле препятствует изменению магнитного потока, вызвавшему этот индукционный ток.
Закон Фарадея с учетом правила Ленца можно сформулировать следующим образом: величина ЭДС электромагнитной индукции 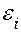 в контуре численно равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную этим контуром, то есть:
в контуре численно равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную этим контуром, то есть:
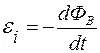 (закон Фарадея с учетом правила Ленца).
(закон Фарадея с учетом правила Ленца).
 2014-02-02
2014-02-02 28382
28382
