1. Скалярное умножение коммутативно, т.е. для любых векторов 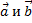 справедливо равенство
справедливо равенство 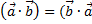 )
)
2. 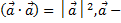 ненулевой вектор, и
ненулевой вектор, и 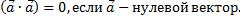
3. 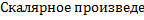 ние равно нулю тогда и только тогда, когда сомножители ортогональны или хотя бы один из них равен нуль-вектору.
ние равно нулю тогда и только тогда, когда сомножители ортогональны или хотя бы один из них равен нуль-вектору.
4. 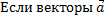 и
и  заданы своими координатами в ортогональном базисе
заданы своими координатами в ортогональном базисе 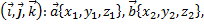 то их скалярное произведение может быть вычислено по формуле
то их скалярное произведение может быть вычислено по формуле 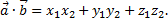
Отсюда следует необходимое и достаточное условие ортогональности векторов: 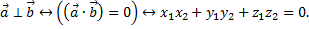
5. Для любых векторов 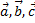 справедливо равенство
справедливо равенство 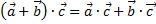 (дистрибутивность операции сложения относительно операции умножения векторов).
(дистрибутивность операции сложения относительно операции умножения векторов).
6. Для любых векторов 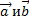 и любого числа k справедливо равенство
и любого числа k справедливо равенство 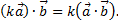 (Ассоциативность по отношению к умножению вектора на число.)
(Ассоциативность по отношению к умножению вектора на число.)
7. Пусть 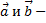 два ненулевых вектора,
два ненулевых вектора, 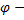 угол между ними. Из определения скалярного произведения следует:
угол между ними. Из определения скалярного произведения следует: 
8. Пусть в пространстве дана некоторая ось 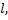 единичный вектор
единичный вектор 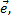 который составляет с координатными осями углы
который составляет с координатными осями углы 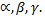 Тогда проекция произвольного вектора
Тогда проекция произвольного вектора 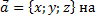 эту ось определяется формулой
эту ось определяется формулой 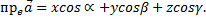
Пример 1. Найти проекцию вектора 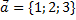 на ось
на ось 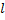 , образующую с координатными осями острые углы.
, образующую с координатными осями острые углы.
Решение. Направляющие косинусы оси 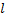 таковы:
таковы: 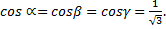
Следовательно, 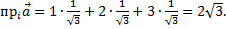
Ответ: 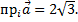
Пример 2. Даны векторы 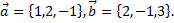 Найти
Найти 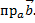
Решение. Так как 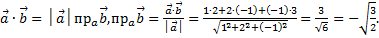
Ответ: 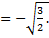
 2015-04-01
2015-04-01 335
335







