Статистическая гипотеза называется параметрической, если в ней сформулированы предположения относительно значений параметров функции распределения известного вида. Если в формулировке гипотезы не встречаются предположения о значениях параметров функции распреде-ления, то такая гипотеза называется непараметрической.
Нулевой гипотезой называют выдвинутую гипотезу и обозначают 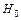 . Альтернативной называется гипотеза, конкурирующая с нулевой гипоте-зой в том смысле, что если отвергается нулевая гипотеза, то принимается альтернативная. Ее обозначают Ha.
. Альтернативной называется гипотеза, конкурирующая с нулевой гипоте-зой в том смысле, что если отвергается нулевая гипотеза, то принимается альтернативная. Ее обозначают Ha.
Суждения относительно истинности (ложности) статистических гипотез формулируются на основании выборки объема n с помощью статистических критериев.
Статистическим критерием называется вспомогательная случайная величина К, с помощью которой принимается решение о принятии либо отклонении нулевой гипотезы.
При проверке статистических гипотез по выборочным данным всегда существует возможность принятия ложного решения. Это объясняется тем, что объем выборки конечен, и поэтому нельзя точно определить ни вид функции распределения, ни значения параметров.
Ошибкой первого рода называется ошибка отклонения верной нулевой гипотезы 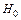 .
.
Уровнем значимости aстатистического критерия называется вероятность совершения ошибки первого рода.
Ошибкой второго рода называется ошибка принятия ложной нулевой гипотезы 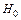 .
.
Мощностью M статистического критерия К называется вероятность несовершения ошибки второго рода, т. е. M = 1 – b.
Будем рассматривать только один вид статистических критериев – статистические критерии значимости. Это значит, что будет заранее фиксироваться вероятность совершения ошибки первого рода (уровень значимости a) и тогда нет необходимости в нахождении ошибки второго рода b. Например, если при отклонении нулевой гипотезы 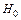 на уровне значимости a = 0,05 мы совершаем ошибку первого рода (считаем правильную нулевую гипотезу
на уровне значимости a = 0,05 мы совершаем ошибку первого рода (считаем правильную нулевую гипотезу 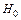 ложной), то в среднем ошибаемся в 5 из 100 случаев применения данного статистического критерия значимости.
ложной), то в среднем ошибаемся в 5 из 100 случаев применения данного статистического критерия значимости.
3 Применение критерия Пирсона c2 для проверки гипотезы
о виде закона распределения случайной величины
Гипотеза о виде закона распределения изучаемой случайной величины обычно выдвигается на основании графического изображения статисти-ческого закона распределения, сведений о механизме формирования значений этой величины, а также на основании значений оценок числовых характеристик.
В таблицах 1 и 2 приведены сведения о наиболее часто используемых при решении практических задач законах распределения дискретных и непрерывных случайных величин. В графе «Примечание» этих таблиц приведены примеры случайных величин, подчиняющихся указанным законам, либо описан механизм формирования значений этих величин.
Если изучается непрерывная случайная величина, то вид гистограммы относительных частот обычно значительно облегчает задачу выдвижения гипотезы H 0. Например, по виду гистограммы, изображённой на рисунке 1, а, логично выдвинуть гипотезу о равномерном законе распределения исследуемой случайной величины. Вид гистограмм, приведённых на рисунках 1, б и 1, в, напоминает соответственно кривые экспоненциального и нормального законов распределения. Большое внимание при выдвижении гипотез уделяется и вычисленным значениям числовых характеристик (примеры 1, 2).
Таблица 1 – Основные сведения о наиболее часто встречающихся на практике
законах распределения дискретных случайных величин
| Название закона распределения | Возможные значения | Параметры | Параметры | Числовые характеристики | Вероятности возможных значений, столбцовая диаграмма | Примечание | ||
| M [ X ] | D [ X ] | s[ X ] | ||||||
| Биномиальный | X = 0, 1, 2,..., n | p, n | 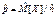 | 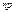 | 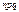 | 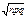 | 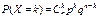 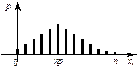 | Случайная величина X характеризует число появлений события A в серии из n независимых испытаний, в каждом из которых это событие может осуществиться с вероятностью p |
 Пуассона Пуассона | X = 0, 1, 2,..., m,... | a | 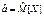 | 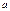 | 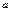 | 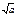 | 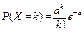 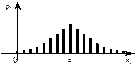 | Пример: число событий простейшего потока, характеризующегося интенсивностью a, где a – число событий, произошедших в течение единицы времени |
| Геометрический | X = 0, 1, 2,..., m,... | p | 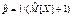 | 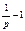 | 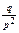 | 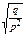 | 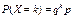 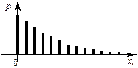 | Случайная величина X характеризует число независимых испытаний, произведённых до первого появления события A, которое в каждом из этих испытаний может произойти с вероятностью p (при этом испытание, в котором появляется событие A, не учитывается) |
| Таблица 2 – Основные сведения о наиболее часто встречающихся на практике | |||||||||
| Закон распре-деления | Возможные значения | Параметры | Статистическая оценка параметров | Числовые характеристики | Вероятность попадания значений с. в. в отрезок [a; b] | ||||
| M [ X ] | D [ X ] | s[ X ] | A [ X ] | Ex [ X ] | |||||
| Равно-мерный | 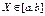 | a b | 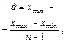 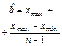 | 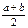 | 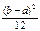 | 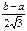 | –1,2 | 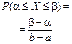 | |
| Экспо-ненци-альный (показа-тельный) | 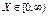 | l | 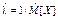 | 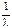 | 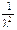 | 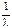 | 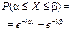 | ||
| Нормаль-ный | 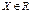 | m s | 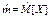 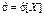 | m | s2 | s | 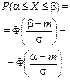 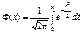 |
Проверка гипотезы о предполагаемом распределении производится с помощью непараметрических критериев значимости. Одной из групп таких критериев значимости являются критерии согласия, с помощью которых проверяются нулевые гипотезы о виде функции распределения случайной величины.
Одним из наиболее широко используемых на практике критериев согласия является критерий c2 Пирсона. Он может использоваться для проверки гипотез о виде закона распределения как дискретных, так и непрерывных случайных величин.
| законах распределения непрерывных случайных величин | ||
| Функция плотности распределения вероятностей | Функция распределения | Примечание |
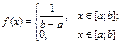 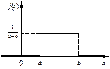 | 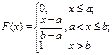 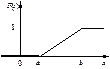 | Если все возможные значения непрерывной случайной величины принадлежат отрезку [ a; b ], и все значения, попадающие на этот отрезок равновозможны, то данная случайная величина X распределена по равномерному закону. Пример: величина погрешности при округлении данных |
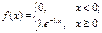 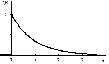 | 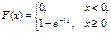 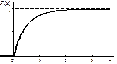 | Примеры: – промежуток времени между моментами наступления двух последовательных событий простейшего потока; – разнообразные временные характеристики функционирования технических устройств (время безотказной работы оборудования и т. д.) |
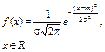 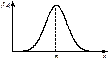 | 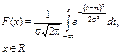  | Если случайная величина X представляет собой сумму большого числа независимых (или слабо зависимых) случайных величин, сопоставимых по уровню своего влияния на суммарный результат, то эта величина имеет распределение, близкое к нормальному Пример: реальные значения параметров изготовленного изделия |
Применение критерия c2 основано на сопоставлении эмпирических mi и теоретических npi (вычисленных в предположении справедливости проверяемой гипотезы) частот попадания значений исследуемой случайной величины в рассматриваемые частичные разряды. В качестве меры расхождения эмпирического и теоретического распределений используется статистика
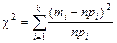 , (1)
, (1)
которая при 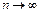 независимо от вида предполагаемого распределения стремится к распределению c2 с
независимо от вида предполагаемого распределения стремится к распределению c2 с 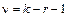 степенями свободы (здесь
степенями свободы (здесь 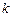 – число разрядов разбиения, r – число параметров теоретического распределения, оцениваемых по выборке).
– число разрядов разбиения, r – число параметров теоретического распределения, оцениваемых по выборке).
Легко заметить, что при незначительных отклонениях значений mi от npi значение критерия c2 будет близким к нулю. И наоборот, большое значение критерия c2 свидетельствует о существенном отклонении значений mi и npi.
| а) | 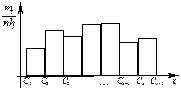 | |||
| б) | 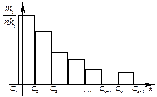 | в) | 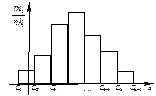 | |
| Рисунок 1 – Примеры гистограмм относительных частот | ||||
Необходимыми условиями применения критерия c2 являются достаточно большой объем выборки (n ³ 30) и отсутствие в теоретическом распределении разрядов с небольшим (npi < 5) числом наблюдений. Для обеспечения последнего условия интервалы, для которых npi < 5, необходимо объединить с соседними. На хвостах распределения допускается значение npi ³ 1.
4 Алгоритм применения критерия c2 для проверки гипотезы
о виде закона распределения исследуемой случайной величины
1 Строится статистический закон распределения случайной величины.
2 Выбирается уровень значимости a.
3 Формулируется гипотеза о виде закона распределения исследуемой случайной величины.
4 Вычисляются теоретические вероятности pi попадания значений случайной величины Х в рассматриваемые разряды разбиения: 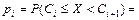
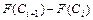 , (
, (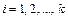 ), где F (x) – гипотетическая функция распределения случайной величины X.
), где F (x) – гипотетическая функция распределения случайной величины X.
Замечание – Если изучается непрерывная случайная величина, то при вычислении значений 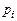 необходимо изменить границы первого и последнего частичных интервалов разбиения таким образом, чтобы учесть все возможные значения, которые может принять случайная величина предполагаемого класса. В зависимости от конкретного вида проверяемой гипотезы границы частичных интервалов необходимо изменить следующим образом:
необходимо изменить границы первого и последнего частичных интервалов разбиения таким образом, чтобы учесть все возможные значения, которые может принять случайная величина предполагаемого класса. В зависимости от конкретного вида проверяемой гипотезы границы частичных интервалов необходимо изменить следующим образом:
| Вид закона распределения | Первый интервал разбиения | Последний интервал разбиения |
| Равномерный | 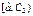 | 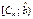 |
| Экспоненциальный | 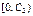 | 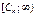 |
| Нормальный | 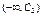 | 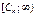 |
Для того чтобы избежать ошибок при вычислении вероятностей 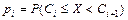 непрерывной случайной величины удобно воспользоваться расчетными таблицами 3–5.
непрерывной случайной величины удобно воспользоваться расчетными таблицами 3–5.
Таблица 3 – Вычисление вероятностей 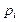 равномерно распределенной случайной величины
равномерно распределенной случайной величины
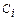 | 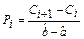 |
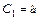 | 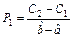 |
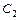 | 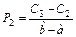 |
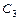 | 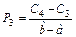 |
| … | … |
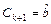 | ––– |
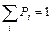 |
Таблица 4 – Вычисление вероятностей 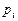 показательно распределенной
показательно распределенной
случайной величины
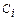 | 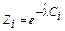 | 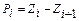 |
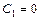 | 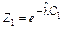 | 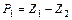 |
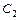 | 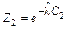 | 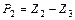 |
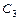 | 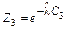 | 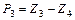 |
| … | … | … |
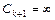 | 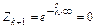 | ––– |
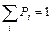 |
Таблица 5 – Вычисление вероятностей 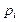 случайной величины, имеющей
случайной величины, имеющей
нормальное распределение
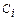 | 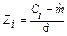 | 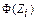 | 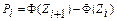 |
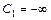 | 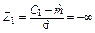 | 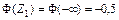 | 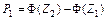 |
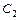 | 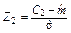 | 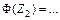 * * | 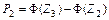 |
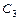 | 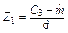 | 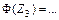 * * | 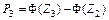 |
| … | … | … | … |
 | 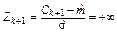 | 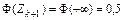 | ––– |
 | |||
* 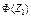 , , 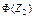 , , 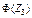 , …, , …, 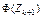 вычисляются по таблице значений функции вычисляются по таблице значений функции 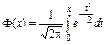 (приложение Г). (приложение Г). |
5 Определяются значения теоретических частот npi (i = 1, 2,…, k). При необходимости для обеспечения условия npi ³ 5 объединяются несколько соседних разрядов разбиения.
6 Вычисляется выборочное значение критерия c2 по формуле (1).
7 По таблице критических точек распределения c2 определяется критическое значение 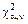 , соответствующее заданному уровню значимости a и числу степеней свободы n = k – r – 1.
, соответствующее заданному уровню значимости a и числу степеней свободы n = k – r – 1.
Если расчётное значение критерия попадает в критическую область, т. е. 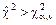 , то проверяемая гипотеза отвергается (при этом вероятность отклонения верной нулевой гипотезы равна a).
, то проверяемая гипотеза отвергается (при этом вероятность отклонения верной нулевой гипотезы равна a).
В случаях, когда наблюденное значение 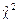 не превышает критического
не превышает критического 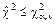 , считают, что выдвинутая гипотеза не противоречит опытным данным. Подчеркнем, что полученный результат свидетельствует лишь о приемлемом согласовании проверяемой гипотезы с имеющимися выборочными данными и в общем случае не является доказательством истинности этой гипотезы.
, считают, что выдвинутая гипотеза не противоречит опытным данным. Подчеркнем, что полученный результат свидетельствует лишь о приемлемом согласовании проверяемой гипотезы с имеющимися выборочными данными и в общем случае не является доказательством истинности этой гипотезы.
Пример 1 На основании выборочных данных, приведённых в примере 1 лабораторной работы № 1, подобрать закон распределения случайной величины X, характеризующей число отказов оборудования, произошедших в течение рабочей смены. Уровень значимости a принять равным 0,05.
Решение. После проведения первичной обработки полученных данных (см. пример 1 лабораторной работы № 1), опираясь на сведения о механизме формирования значений исследуемой случайной величины (поток отказов оборудования обычно обладает свойствами простейшего потока), учитывая вид построенной столбцовой диаграммы и значения оценок числовых характеристик  , то есть
, то есть 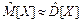 , выдвигаем гипотезу о том, что изучаемая случайная величина подчиняется закону распределения Пуассона:
, выдвигаем гипотезу о том, что изучаемая случайная величина подчиняется закону распределения Пуассона:
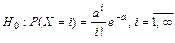 ;
;
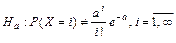 .
.
Для проверки этой гипотезы с помощью критерия c2 выполним следующие действия.
Вычислим оценку параметра a распределения Пуассона: 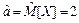 .
.
Вычислим вероятности наблюденных значений изучаемой случайной величины: 
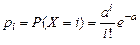 (i = 0, 1, 2,…, 6, …);
(i = 0, 1, 2,…, 6, …);
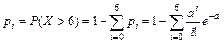 (i = 7);
(i = 7);
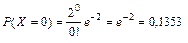 ;
; 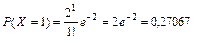 ;
;
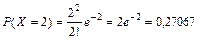 ;
; 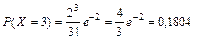 ;
;
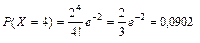 ;
; 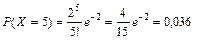 ;
;
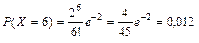 ;
;
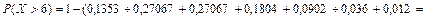
= 1 – 0,9948 = 0,0052.
Заполним расчётную таблицу:
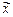 | >6 | |||||||
| mi | ||||||||
| pi | 0,1353 | 0,27067 | 0,27067 | 0,1804 | 0,0902 | 0,036 | 0,012 | 0,0052 |
| npi | 6,765 | 13,5335 | 13,5335 |  9,02 9,02 | 4,51 | 1,8 | 0,6 | 0,26 |
Учитывая, что теоретические частоты наблюденных значений, находящихся в трех последних столбцах таблицы, не превышают трех единиц, при вычислении значения критерия c2 эти разряды объединим в один:
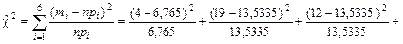
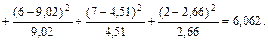
По таблицам квантилей распределения c2 определим критическое значение 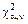 , соответствующее a = 0,05, n = k – r – 1 = 6 – 1 – 1 = 4:
, соответствующее a = 0,05, n = k – r – 1 = 6 – 1 – 1 = 4: 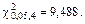
Поскольку выборочное значение критерия меньше критического 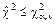 , можно сделать вывод о том, что гипотеза не противоречит экспериментальным данным; поэтому нет оснований для отклонения проверяемой гипотезы.
, можно сделать вывод о том, что гипотеза не противоречит экспериментальным данным; поэтому нет оснований для отклонения проверяемой гипотезы.
Пример 2 На основании опытных данных, приведённых в примере 2 лабораторной работы № 1, подобрать закон распределения непрерывной случайной величины X, характеризующей время безотказной работы оборудования между двумя последовательными переналадками. Уровень значимости a принять равным 0,05.
Решение. Используя результаты первичной обработки выборочных данных (вид полученной гистограммы и значения оценок числовых характеристик: 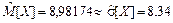 ), а также учитывая сведения о физическом смысле полученных значений, выдвигаем гипотезу о том, что случайная величина X распределена по экспоненциальному закону:
), а также учитывая сведения о физическом смысле полученных значений, выдвигаем гипотезу о том, что случайная величина X распределена по экспоненциальному закону:
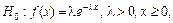
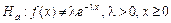 .
.
Проверим согласование сформулированной гипотезы 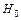 с экспериментальными данными с помощью критерия c2.
с экспериментальными данными с помощью критерия c2.
Вычислим оценку параметра экспоненциального закона распределения:
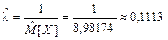 .
.
При вычислении вероятностей pi = P (Ci £ X < Ci +1) изменим границы первого и последнего интервалов разбиения в соответствии с замечанием, приведенным на странице 34.
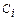 | 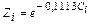 | 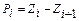 |
| 0,2828 | ||
| 2,987 | 0,7172 | 0,3124 |
| 8,127 | 0,4047 | 0,1763 |
| 13,267 | 0,2284 | 0,0995 |
| 18,407 | 0,1289 | 0,0562 |
| 23,547 | 0,0727 | 0,0317 |
| 28,687 | 0,0410 | 0,0179 |
| 33,827 | 0,0232 | 0,0232 |
 | ––– | |
 |
Определим значения теоретических частот и занесём их в расчётную таблицу:
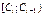 | [0; 2,987) | [2,987; 8,127) | [8,127; 13,267) | [13,267; 18,407) | [18,407; 23,547) | [23,547; 28,687) | [28,687; 33,827) | [33,827; ¥) |
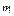 | ||||||||
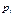 | 0,2828 | 0,3124 | 0,1763 | 0,0995 | 0,0562 | 0,0317 | 0,0179 | 0,0232 |
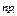 | 14,140 | 15,620 | 8,815 | 4,975 | 2,810 | 1,585 | 0,895 | 1,160 |
 |
Поскольку значения npi, соответствующие четырем последним интервалам разбиения, не превышают пяти единиц, объединим эти интервалы в один и для вычисления значения критерия c2 составим следующую расчётную таблицу:
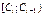 | [0; 2,987) | [2,987; 8,127) | [8,127; 13,267) | [13,267; 18,407) | [18,407; ¥) |
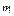 | |||||
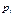 | 0,2828 | 0,3124 | 0,1763 | 0,0995 | 0,1290 |
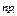 | 14,140 | 15,620 | 8,815 | 4,975 | 6,450 |
Вычислим значение критерия c2:
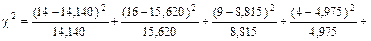
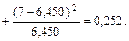
Критическое значение критерия, соответствующее значениям a = 0,05 и 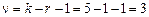 , определим с помощью приложения В:
, определим с помощью приложения В: 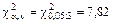 .
.
Поскольку 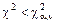 , можно сделать вывод о том, что проверяемая гипотеза об экспоненциальном законе распределения изучаемой случайной величины Х не противоречит экспериментальным данным и нет основания для отклонения нулевой гипотезы.
, можно сделать вывод о том, что проверяемая гипотеза об экспоненциальном законе распределения изучаемой случайной величины Х не противоречит экспериментальным данным и нет основания для отклонения нулевой гипотезы.
1 Получить выборку значений исследуемой случайной величины X с указанным значением уровня значимости a и записать её на диск (см. приложение А, п. 2).
2 Произвести первичную обработку полученных статистических данных.
3 Выдвинуть гипотезу о виде закона распределения изучаемой случайной величины.
4 Проверить согласование сформулированной гипотезы с имеющимися выборочными данными (ручной расчёт):
– вычислить оценки параметров предполагаемого закона распределения;
– если рассматривается дискретная случайная величина, то вычислить вероятности всех возможных значений случайной величины 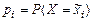 . Если рассматривается непрерывная случайная величина, то вычислить вероятности попадания значений случайной величины в i- й интервал
. Если рассматривается непрерывная случайная величина, то вычислить вероятности попадания значений случайной величины в i- й интервал 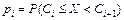 , i = 1, 2, …, k;
, i = 1, 2, …, k;
– определить значения теоретических частот npi, i = 1, 2, …, k;
– вычислить выборочное значение критерия c2;
– сравнить выборочное значение критерия с критическим значением 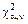 и сделать вывод.
и сделать вывод.
5 Проверить согласование выдвинутой гипотезы с имеющимися экспериментальными данными с помощью ППП:
– вычислить выборочное значение критерия c2 (приложение А, п. 9);
– построить совместное графическое изображение статистического и предполагаемого теоретического распределений изучаемой случайной величины (см. приложение А, п. 9).
6 Сделать вывод о законе распределения вероятностей изучаемой случайной величины.
Контрольные вопросы
1 Что такое непараметрическая гипотеза?
2 Что такое нулевая, альтернативная гипотезы?
3 Из каких соображений выдвигается гипотеза о виде закона распределения случайной величины?
4 Что такое статистический критерий?
5 Какие ошибки могут быть совершены при статистической проверке гипотез?
6 Что такое уровень значимости статистического критерия?
7 Что называется статистическим критерием значимости?
8 По какой формуле вычисляется критерий c2?
9 Сформулируйте алгоритм применения критерия Пирсона.
10 Как найти критическое значение критерия 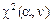 ?
?
11 Как вычислить число степеней свободы  ?
?
 2015-04-08
2015-04-08 4839
4839
