Независимое поведение олигополистов: объемная конкуренция. Модель дуополии Курно

Анализ дуополии как простейшей формы олигополии впервые был предложен в 1838 г. французским экономистом, математиком и философом Огюстеном Курно. Дуополия - это рыночная структура, при которой два продавца, защищенные от появления дополнительных продавцов, являются единственными производителями стандартизированной продукции, не имеющей близких заменителей. Экономические модели дуополии полезны, чтобы проиллюстрировать, как предположения отдельного продавца насчет ответа соперника воздействуют на равновесный выпуск. Эта модель допускает, что каждый из двух продавцов предполагает, что его конкурент всегда будет удерживать свой выпуск неизменным на текущем уровне. Она также предполагает, что продавцы не узнают о своих ошибках. В действительности предположения продавцов о реакции конкурента, вероятно, поменяются, когда они узнают о своих предыдущих ошибках.

Модель Курно базируется на следующих предпосылках:

1) Две фирмы производят однородный товар.

2) Фирмам известна кривая рыночного спроса.

3) Фирмы принимают решения о производстве независимо друг от друга и одновременно.

4) Каждая из фирм предполагает выпуск конкурента постоянным.

Положим, что каждый дуополист (во всех отношениях идентичный сопернику) стремится к максимизации своей прибыли, исходя из предположения, что другой дуополист не изменит выпуск, каким бы он ни был. Иными словами, предположительные вариации каждого имеют нулевую оценку (dq₂/dq₁ = dq₁/dq₂=0). Допустим, что обратная функция рыночного спроса линейна:

P = a – bQ, (6.1)

где

Q = q₁ +q₂. (6.2)

Подставив (5.2) в (5.1), получим:

P = a – b(q₁ + q₂).

Тогда прибыли дуополистов можно представить как разность между выручкой и затратами каждого из них:

p₁ = TR₁ – cq₁ = Pq₁ – cq₁; (6.3)

p₂ = TR₂ – cq₂ = Pq₂ – cq₂.

Подставив в правые части уравнений (6.3) значение P из уравнения (6.1), получим:

p₁ = aq₁ – bq₁² – bq₁q₂ - cq₁ ;(6.4)

p₁ = aq₂ – bq₂² – bq₁q₂ – cq₂.

Условием максимизации прибылей дуополистов будет равенство нулю первых производных уравнений (6.4):

;

,

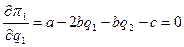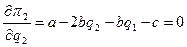откуда

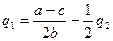; (6.5)

.

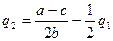Это и есть уравнения кривых реагирования дуополистов. На рис. 6.1 им соответствуют линии R₁(q₂)=q₁ и R₂(q₁)=q₂. Равновесные выпуски Курно определяются из решения системы (6.5):

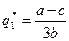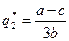, , (6.6)

и следовательно, .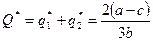

Равновесные точки дуополистов q₁^* и q₂^* и являются координатами точки равновесия выпусков Курно-Нэша (точка C-N).

Говорят, что рынок находится в состоянии Нэша, если каждое предприятие придерживается стратегии, являющейся лучшим ответом на стратегии, которым следуют другие предприятия отрасли. То есть рынок находится в состоянии равновесия Нэша, если ни одно предприятие не желает изменить своего положения в одностороннем порядке.

Поскольку вторые производные функций прибыли меньше нуля (),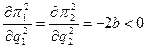

то условие максимизации прибылей дуополистов выполняется и, следовательно, выпуски q₁^* и q₂^* действительно обеспечивают максимумы прибыли дуополистам.

Подставив значения равновесных выпусков в выражение (6.1), найдем значение равновесной цены дуополии Курно:

.

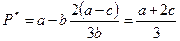Следовательно, равновесные цены и объемы выпуска дуополистов Курно одинаковы, что объясняется однородностью их продуктов (близостью товаров-субститутов) и равенством их затрат на производство.

Модель дуополии Курно может быть распространена на отрасль с любым количеством идентичных фирм. В случае монополии, когда в отрасли действует одно предприятие, то прибылемаксимизирующий выпуск монополиста (например, q₂ = 0 в выражении 6.5) составит

,

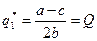а оптимальная для монополиста цена будет равна

.

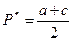Обобщая результаты на N фирм в отрасли (ввиду симметрии всех предприятий), получим:

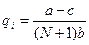, i = 1,…, N; , .

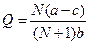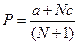В пределе, по мере того, как число фирм приближается к бесконечности, равновесие Курно стремится к равновесию в условиях совершенной конкуренции. Если N ® ¥, индивидуальные объемы q_i ® 0, а цены P ® c, то эти значения являются конкурентным равновесием, при котором каждая фирма производит ничтожно малое количество продукции и поэтому не влияет на цену товара; в этом случае цена товара равна предельным издержкам.

В таблице 6.1 приведены равновесные выпуски (отраслевые объемы) и цены для случая в монополии (n = 1), дуополии Курно (n = 2), n = N симметричных предприятий и совершенной конкуренции ().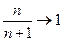

Таблица 6.1 Равновесные объемы выпуска и цены

n		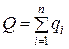P
n = 1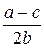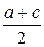
n = 2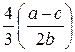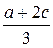
n = N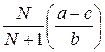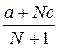

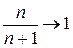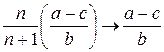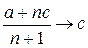Заметим, что отраслевой выпуск в дуополии Курно выше, чем в случае монополии; а равновесная цена продукции при равновесии Курно, напротив, будет ниже, чем при монополии. Из таблицы 6.1 следует, что с ростом N цена снижается, а отраслевой выпуск растет. Таким образом, модель Курно предсказывает снижение цены продукции и приближение ее к величине предельных затрат при достаточно большом числе предприятий-производителей.

Динамику или приближение к равновесию путем серии последовательных шагов можно анализировать с помощью кривых реакции, которые показывают оптимальный выпуск продукции каждой фирмой при заданных выпусках продукции конкурентом. Предположим, что временной лаг равен одному периоду. Используя уравнения для равновесия Курно, запишем формулы для кривых реакции:

, .

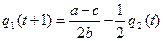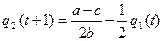Решением этой пары разностных уравнений являются траектории движения двух выпусков во времени. Кривые реакции и траектории показаны на рис. 6.2. Так, начиная из точки с координатами (0,`q<sub>2</sub>) (решение о такой величине выпуска первым принял дуополист 2) первый дуополист устанавливает выпуск продукции на уровне ` q₁, тогда второй дуополист в ответ на это изменяет свой выпуск, а первый «подгоняет» свой выпуск под выпуск второго дуополиста и т.д. до тех пор, пока не будет достигнута точка равновесия Курно. На каждом шаге этого процесса динамической подгонки изменение выпуска одной фирмы вызывает изменение выпуска другой.

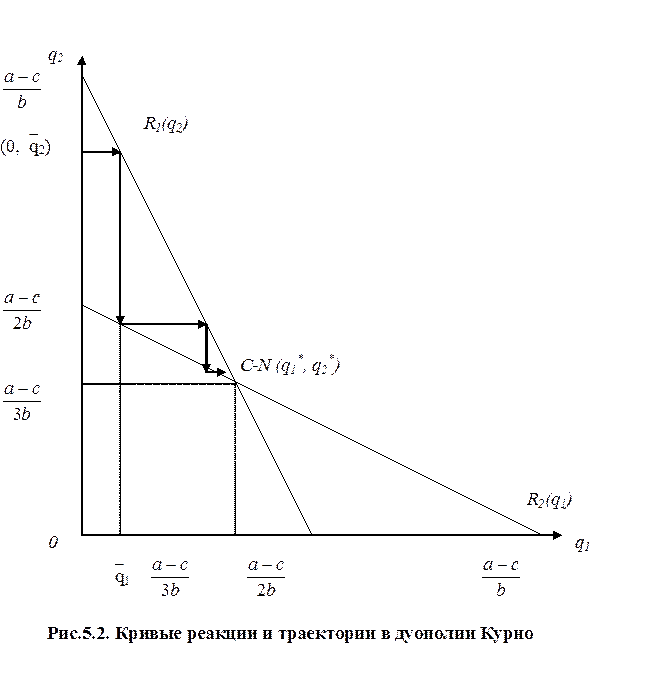5.3. Модель дуо6олию Штакельберга

В рассмотренных выше моделях Курно предполагалось, что фирмы обладают одинаковой рыночной силой, и их поведение определяется одновременно. Рассмотрим теперь ситуацию, когда фирмы неодинаковы по силе, а выбор объема производства осуществляется последовательно: сначала объем производства определяется для более «сильной» фирмы, затем «слабая» фирма выбирает свою линию поведения.

Модель асимметричной дуополии, предложенная Штакельбергом в 1934 г., представляет развитие моделей количественной дуополии Курно. Асимметрия дуополии Штакельберга заключается в том, что дуополисты могут придерживаться разных типов поведения: стремиться быть «лидером» или оставаться «последователем». «Последователь» Штакельберга придерживается предположений Курно, он следует своей кривой реагирования и принимает решения о прибылемаксимизирующем выпуске, полагая выпуск соперника заданным. «Лидер» Штакельберга, напротив, не столь наивен, как обыкновенный дуополист Курно. Он хорошо понимает рыночную ситуацию и не только знает кривую реагирования соперника, но и инкорпорирует ее в свою функцию прибыли, так что последняя принимает вид

p_i = f(q_i, R_j(q_i)),

где R_j(q_i) – кривая реагирования дуополиста j на величину выпуска, предложенного дуополистом i.

В случае дуополии возможны четыре комбинации двух типов поведения:

1) дуополист 1 – «лидер», дуополист 2 – «последователь»;

2) дуополист 2 – «лидер», дуополист 1 – «последователь»;

3) оба дуополиста – «последователи»;

4) оба дуополиста – «лидеры».

Случаи 1 и 2 симметричны. Случай 3 в содержательном смысле есть ситуация дуополии Курно, когда каждый из дуополистов руководствуется своими кривыми реагирования, а в случае 4 каждый из дуополистов, стремясь стать «лидером», определяет максимум своей прибыли исходя из предположения, что он является «лидером», а соперник – «последователем». Результат подобного взаимодействия – неравновесие по Штаккельбергу, ведущее к развязыванию ценовой войны, которая ведет либо к отказу одного из дуополистов от роли «лидера», либо к достижению между ними сговора.

Рассмотрим случай 1. Представим функцию «лидера» для дуополиста 1 в виде

p₁ = f(q₁, R₂(q₁)). (6.7)

При описании уравнения прибыли дуополиста 1 воспользуемся выражением (6.6), подставив в него значение q₂, т.е. уравнение кривой реагирования дуополиста 2, которой соответствует линия R₂(q₁) на рис. 6.2. Тогда уравнение прибыли примет вид

,

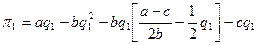что равносильно

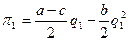
Максимум прибыли находим, решая уравнение

,

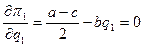откуда

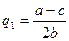. (6.8)

Это и есть оптимальный выпуск «лидера» в модели Штаккельберга. Прибылемаксимизирующий выпуск «последователя» получим, подставив значение выпуска дуополиста 1 (6.8) в уравнение кривой реагирования дуополиста 2 (5.5):

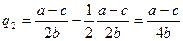
Таким образом, прибылемаксимизирующий выпуск «последователя» вдвое ниже прибылемаксимизирующего выпуска «лидера». Общий выпуск «лидера» и «последователя» равен

.

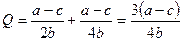Используя значение отраслевого выпуска, с помощью обратной функции рыночного спроса найдем равновесную цену олигополии в модели Штаккельберга для случая «лидера» и «последователя». Она будет равна

.

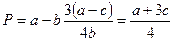Величины Q = q₁ +q₂ и P называют параметрами равновесия по Штаккельбергу.

Определим прибыли «лидера» и «последователя» в условиях равновесия:

,

,

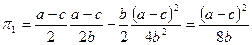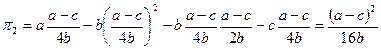откуда p₁ = 2p₂.

Заметим, что прибыль «лидера» вдвое превышает прибыль «последователя», будь то дуополист 1 или 2. Стратегическое поведение «лидера», учитывающее будущую реакцию конкурента на рынке, приносит ему «преимущество первого хода». Поэтому-то и тот и другой предпочтут оказаться лидерами.

Графическая иллюстрация равновесия по Штаккельбергу для дуополии представлена на рис. 6.3.

Ниже приведены основные параметры равновесия Штакельберга:

Выпуск	Прибыль	Рыночная цена
лидера	последователя	отрасли	лидера	последователя
(a - c)/2 b	(a - c)/4 b	3(a - c)/4 b	(a - c)2/8 b	(a - c)2/16 b	(a +3 c)/4

Когда обе фирмы придерживаются предположительных изменений по Курно, равновесие будет в точке С – на пересечении двух кривых реакции. В этом случае q₁ = q₂ = (a-c)/3b. Предположим, что на увеличение выпуска фирмой 1 фирма 2 отвечает в соответствии с ее кривой реакции R₂(q₁). Тогда фирма 1 может увеличить объем производства чему соответствует более высокая кривая изоприбыли p₁¹ на рис. 6.5. Точка касания S является точкой равновесия по Штаккельбергу. Поскольку фирма 1 принимает на себя инициативу в определении объема производства, то она является «лидером» по Штаккельбергу; фирма 2, принимая производство «лидера» как данный факт, является «последователем».

При отсутствии существенного конкурентного преимущества у одной фирмы перед другой неравенство прибыли приведет к ситуации, когда оба дуополиста предпочтут оказаться лидерами (случай 4). Но тогда значения прибылемаксимизирующих выпусков обоих стремящихся стать лидерами дуополистов определяются значением (6.8), а их подстановка в уравнение линейной обратной функции спроса определяет цену:

.

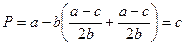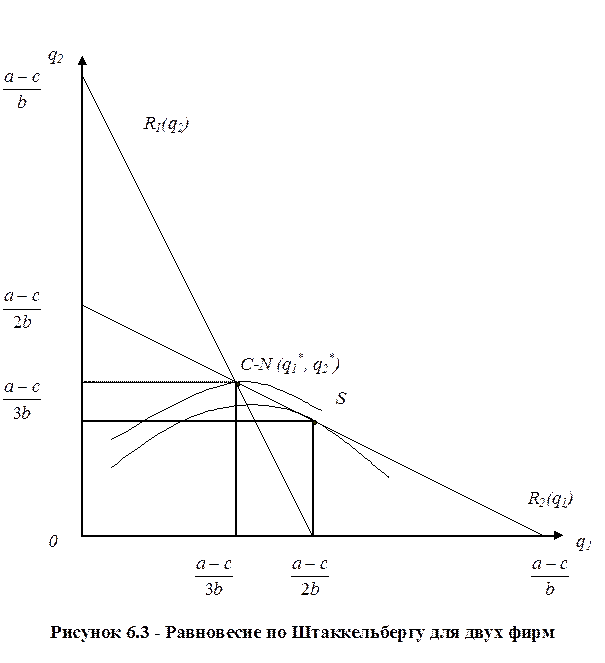
Это равенство цены предельным затратам означает, что прибыль дуополистов равна нулю, что несовместимо с выводом о стабильности. Таким образом, при некотором изменении предположений о поведении дуополистов ситуация переходит в неравновесие.

Другим примером неравновесия дуополии в модели Штаккельберга, при котором фирмы имеют положительные прибыли, может служить ситуация, когда обе фирмы считают, что конкурент будет вести себя как дуополист в модели Курно. Пусть фирма 1 считает, что фирма 2 будет реагировать соответственно кривой реакции Курно, а фирма 2 полагает, что фирма 1 будет реагировать соответственно кривой реакции Курно, т.е.

;

.

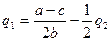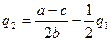Тогда предположительные вариации соответствуют компенсирующему поведению и будут равны

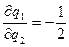и ,

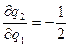поэтому

;

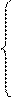
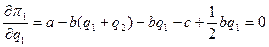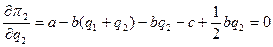(6.9)

и кривые реакции фирм имеют следующий вид:

, .

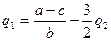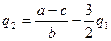В результате получим неравновесие по Штаккельбергу

, ,

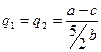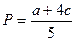при котором обе фирмы получают меньшую прибыль, чем при равновесии по Курно (равновесие по Курно имеет место в точке переключения с компенсирующего на параллельное поведение). При этом

.

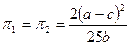На рис. 5.4 приведены кривые реакции и изопрофиты для каждой фирмы. Согласно свойствам изопрофит, прибыль фирмы возрастает по мере увеличения по соответствующей оси объема выпуска и достигает максимума в «монопольной точке».

Равновесие по Штаккельбергу для фирмы 1 S₁ на рис. 6.6 соответствует точке касания кривой равной прибыли для фирмы 1 с кривой реакции фирмы 2, а для фирмы 2 – в точке S₂, в которой кривая равной прибыли для фирмы 2 касается кривой реакции 1 фирмы. Точка неравновесия Штаккельберга лежит выше точки равновесия по Курно.

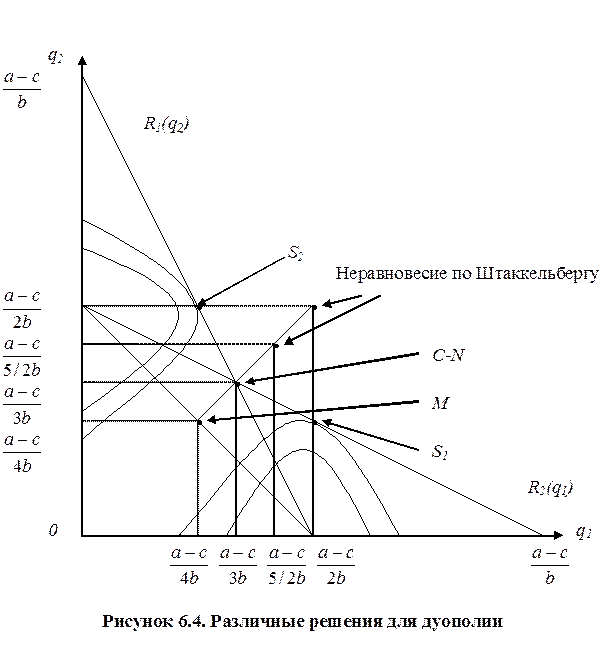
Таким образом, существуют различные модели олигополии. Применение той или иной модели при анализе рынка зависит от характеристик рынка и возможностей фирмы влиять на рыночную цену или объем выпуска. Модели Курно и Штакельберга применяются при исследованиях рынков, когда у фирм существуют фиксированные производственные планы, так что относительно трудно изменить количество выпускаемого продукта, если план уже принят. Это характерно для отраслей с длительным сроком изготовления товара (тяжелая промышленность, самолетостроение, производство уникального оборудования, судостроение и т.д.), а также для тех отраслей, где фирмам необходимо инвестировать значительные средства в специализированное оборудование для сбыта данного товара (например, строительство крупного универмага). На таких рынках изменение цен товаров более вероятно, чем изменение объемов продаж. Модель Бертрана и Эджуорта применяются в тех случаях, когда фирмам сложнее корректировать принятые цены. Примерами могут служить продажи по каталогам, тендеры, аукционы, причем преимущественно в отраслях, производящих товары потребительского назначения. В этом случае, напротив, изменение цен менее вероятно, чем изменение объемов продаж.

Модель Бертрана в отличие от моделей Курно и Штакельберга предполагают наличие ценового взаимодействия фирм на олигополистическом рынке. Таким образом конкуренция заключается в том, что каждая фирма устанавливает свою цену