Формула Бернулли

Пусть производятся n независимых испытаний, в каждом из которых может произойти некоторое событие A с одной и той же вероятностью 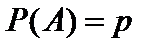или произойти противоположное событие 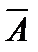с вероятностью 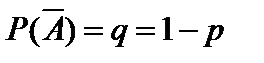. Тогда вероятность того, что событие A наступит ровно k раз, находится по формуле Бернулли:

.

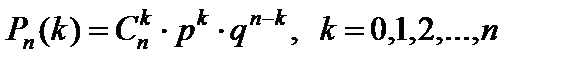Пример 2.1. Игральный кубик подбрасывают 10 раз. Какова вероятность того, что шесть очков выпадет два раза?

Решение

По условию n = 10, k = 2, 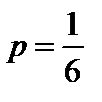, 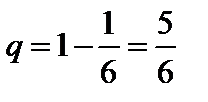. Воспользуемся формулой Бернулли:

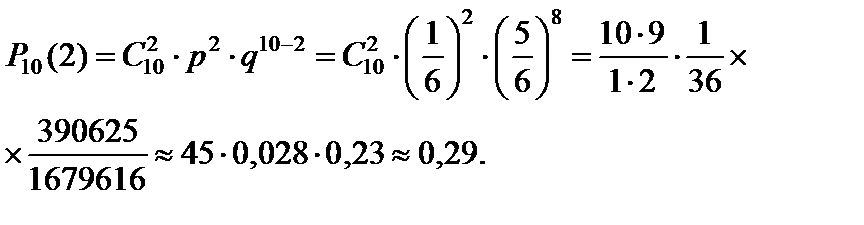
Ответ: 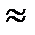0,29.

Пример 2.2. Производится 6 выстрелов по цели. Вероятность попадания в цель при каждом выстреле равна 0,4. Найти вероятность того, что:

1) произойдет одно попадание в цель;

2) произойдет не менее 4 попаданий;

3) произойдет хотя бы одно попадание.

Решение

По условию, n = 6, p = 0,4, q = 1 – 0,4 = 0,6.

1. k = 1. По формуле Бернулли:

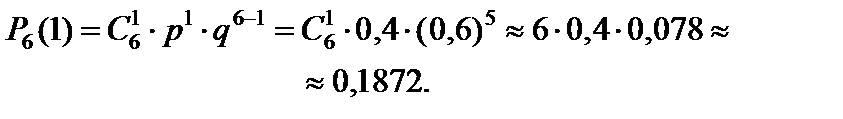
2. Обозначим через В событие «произойдет не менее 4 попаданий в цель». Событие В означает, что было либо четыре попадания, либо пять попаданий, либо шесть попаданий в цель. Следовательно,

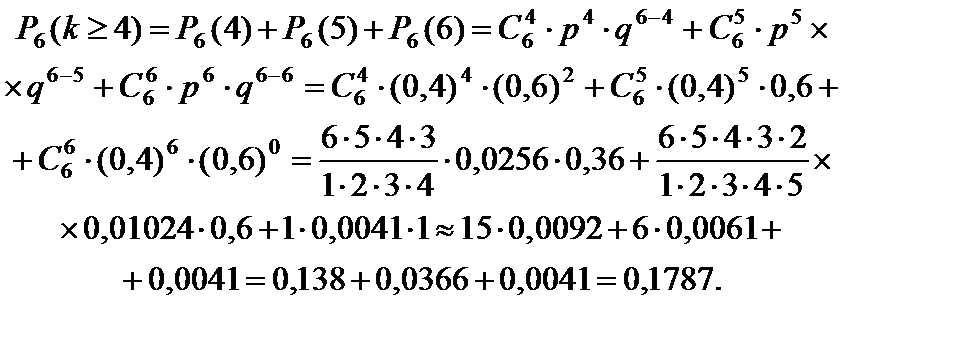
3. События «произойдет хотя бы одно попадание в цель» и «из шести выстрелов нет ни одного попадания в цель» противоположны, поэтому вероятность того, что при 6 выстрелах по цели произойдет хотя бы одно попадание, равна:

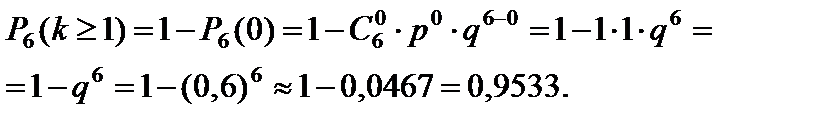
Ответ: 1) 0,1872; 2) 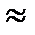0,1787; 3) 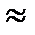0,9533.

Тест 2.1. Вероятность попадания в цель при одном выстреле равна 0,8. Вероятность того (по формуле Бернулли), что в серии из четырех выстрелов будет хотя бы одно попадание, равна:

1) ;

2) ;

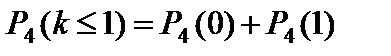3) ;

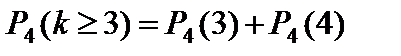4) ;

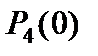5) .

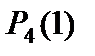Непосредственное применение формулы Бернулли при большом числе испытаний связано с громоздкими вычислениями. Поэтому при больших n вместо нее, как правило, используют приближенные формулы Пуассона и Муавра-Лапласа.