Основы теории теплообмена.
Теплопередача – наука, занимающаяся изучением теплообмена между телами и распределением температуры в телах.
Основные формы передачи теплоты:
1. Теплопроводность.
Теплопроводность представляет собой процесс передачи теплоты путем непосредственного соприкосновения тел или отдельных частей тела, имеющих различную температуру. При этом процесс теплообмена происходит за счет передачи энергии микродвижения одних частиц другим.
В чистом виде теплопроводность наблюдается в твердых телах, а также в неподвижных газах и жидкостях в том случае, когда в них отсутствует конвекция.
Тепловой поток 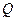 ,
, 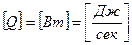 .
.
Закон Фурье: тепловой поток пропорционален градиенту температуры и площади, то есть 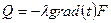 .
.
Плотность теплового потока 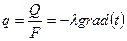 ,
, 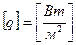 .
.
Коэффициент теплопроводности 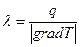 - количество теплоты, которое проходит в единицу времени через единицу поверхности через единичную толщину стенки при перепаде температуры в один градус,
- количество теплоты, которое проходит в единицу времени через единицу поверхности через единичную толщину стенки при перепаде температуры в один градус, 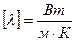 .
.
Конвективный теплообмен – процесс передачи теплоты, который осуществляется в пространстве (в объёме), за счёт движения макро частиц.
В этом процессе идёт совместное действие конвекции (движения) и передачи теплоты за счёт теплопроводности.
Уравнение Ньютона: 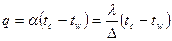 , где
, где 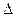 - толщина приграничного слоя, в котором теплопередача происходит за счёт теплопроводности;
- толщина приграничного слоя, в котором теплопередача происходит за счёт теплопроводности; 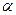 - коэффициент конвективного теплообмена,
- коэффициент конвективного теплообмена, 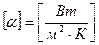 .
.
Лучистый теплообмен – передача теплоты осуществляется в пространстве за счёт энергии электромагнитных волн.
Закон Стефана-Больцмана: 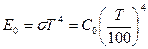 , где
, где 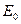 - интенсивность излучения абсолютно чёрного тела.
- интенсивность излучения абсолютно чёрного тела.
Уравнение Ньютона-Рихмана: 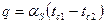 , где
, где 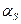 - коэффициент лучистого теплообмена.
- коэффициент лучистого теплообмена.
Теплопроводность.
Температурное поле – совокупность значений температур в отдельных точках тела в зависимости от времени и пространственных координат.
Математическая запись нестационарного трёхмерного температурного поля: 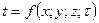 . Математическая запись стационарного трёхмерного поля:
. Математическая запись стационарного трёхмерного поля: 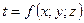 . Это поле называется стационарным, так как
. Это поле называется стационарным, так как 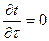 .
.
Изотермическая поверхность – геометрическое место точек имеющих одинаковую температуру.
Изотерма – пересечение изотермической поверхности с перпендикулярной плоскостью.
Изотермическая поверхность либо замыкается внутри тела, либо обрывается на его границе.

Температурный градиент есть вектор направленный по нормали к изотермической поверхности в сторону возрастания температуры и численно равный пределу отношения изменения температуры 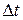 к расстоянию между изотермами по нормали
к расстоянию между изотермами по нормали 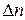 (0С/м)
(0С/м)

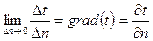
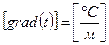
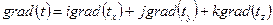
Закон Фурье: 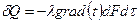
Тепловой поток: 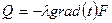 ,
, 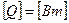 .
.
Плотность теплового потока: 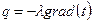 ,
, 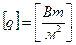 ,
, 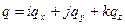 .
.
Задачи теории теплопроводности:
1. Найти нестационарное трёхмерной температурное поле, 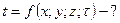 .
.
2. Найти тепловой поток и плотность теплового потока, 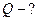 ,
, 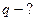 .
.
Вопрос №32
Дифференциальное уравнение теплопроводности.
Условности:
1. Теплофизические свойства системы: 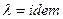 ,
, 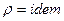 ,
, 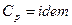 .
.
2. Микрочастицы тела неподвижны.
3. Внутренние источники теплоты распределены в теле равномерно.
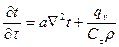 , где
, где 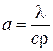 – коэффициент температуропроводности, характеризующий скорость изменения температуры в любой точке тела,
– коэффициент температуропроводности, характеризующий скорость изменения температуры в любой точке тела, 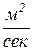 ;
;
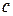 – теплоемкость тела;
– теплоемкость тела; 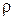 – плотность тела;
– плотность тела; 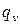 – объемная плотность тепловыделения, вm/м3;
– объемная плотность тепловыделения, вm/м3; 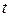 – температура;
– температура; 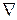 – оператор Лапласа.
– оператор Лапласа.
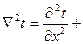
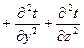 (для полярных координат
(для полярных координат 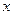 ,
, 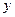 ,
, 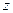 ),
), 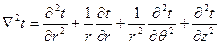 .
.
Условия однозначности – математическое описание частных особенностей рассматриваемого процесса.
Решая уравнение 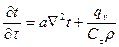 , получим общее решение, которое в совокупности с условиями однозначности даст нам частные решения.
, получим общее решение, которое в совокупности с условиями однозначности даст нам частные решения.
Условные однозначности:
1. Геометрические условия:
a. Форма тела:
i. Плоское тело.
ii. Цилиндрическое тело.
iii. Сферическое тело.
b. Ограниченное тело.
c. Неограниченное тело.
2. Физические условия:
a. Характер изменения физических параметров:
i. Характер изменения 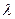 .
.
ii. Характер изменения 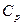 .
.
iii. Характер изменения 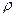 .
.
iv. Характер изменения 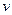 .
.
3. Начальные условия (временные):
a. 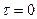 :
:
i. 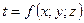 .
.
ii. 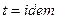 .
.
b. 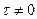 .
.
4. Граничные условия:
a. Граничные условия первого рода – закон изменения температуры на границе тела:
i. 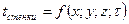 .
.
ii. 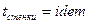 .
.
b. Граничные условия второго тела – закон изменения температурного потока в стенке тела:
i. 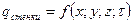 .
.
ii. 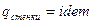 .
.
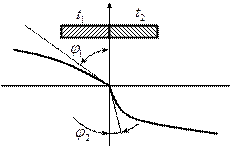
c. Граничные условия третьего рода:
i. Закон изменения температуры окружающей среды.
ii. Закон, по которому идёт теплообмен тела с окружающей средой, 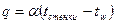 .
.
d. Граничные условия четвёртого рода, 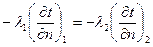 .
.
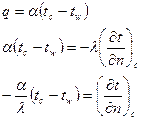
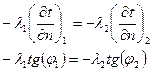
Вопрос №33
1. Плоская стенка.
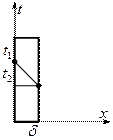 Дано:
Дано: 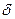 ,
, 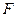 ,
, 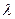 .
.
Найти: 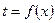 ,
, 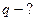 ,
, 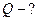 .
.
Решение:
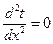
Общее решение: 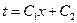 .
.
Граничные условия: 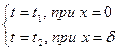 .
.
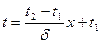
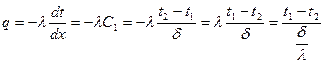
Термическое сопротивление плоской стенки - 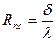 .
.
Отношение 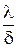 называется тепловой проводимостью стенки.
называется тепловой проводимостью стенки.
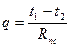
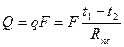
Вопрос №34
Рассмотрим передачу тепла теплопроводностью через плоскую трехслойную стенку (рис. 2б) при условиях: толщина слоев стенки 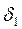 ,
, 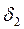 ,
, 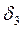 ;
;
коэффициенты теплопроводности материалов соответственно 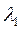 ,
, 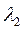 ,
, 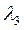 ; контакт между стенками идеальный и температура на границе смежных слоев одинакова. Перенос тепла происходит в стационарных условиях – плотность теплового потока по всем слоям стенки имеет одно и то же значение (q=idem). В этих условиях:
; контакт между стенками идеальный и температура на границе смежных слоев одинакова. Перенос тепла происходит в стационарных условиях – плотность теплового потока по всем слоям стенки имеет одно и то же значение (q=idem). В этих условиях:
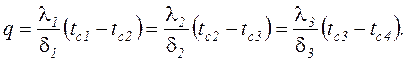
Выделим из этого ряда равенств разности температур (падение температуры по слоям стенки)
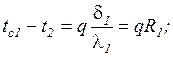
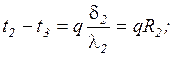
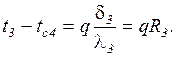
Складывая левые и правые части уравнений разности температур, получаем слева изменение температуры в стенке 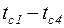 , справа – произведение плотности теплового потока q и общего термического сопротивления
, справа – произведение плотности теплового потока q и общего термического сопротивления 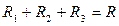
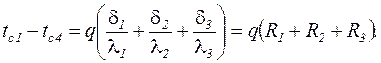
Таким образом, для плотности теплового потока при переносе тепла теплопроводностью через плоскую трехслойную стенку получим следующее выражение:
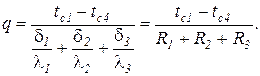
В общем случае для стенки, состоящей из n – слоев, это выражение запишется так:
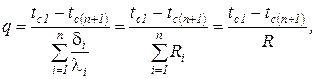
где R – общее термическое сопротивление многослойной стенки.
Вопрос №35
Количество теплоты, отдаваемое жидкостью твердой стенке или воспринимаемое жидкостью от стенки, определяется уравнением Ньютона–Рихмана
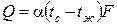 ,
,
а плотность теплового потока следующим образом
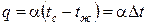
где α – коэффициент, характеризующий условия теплообмена между жидкостью и поверхностью твердого тела, называемый коэффициентом теплоотдачи, Вт/(м2·°C); 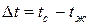 – температурный напор, 0С.
– температурный напор, 0С.
В соответствии с формулой (61) по своему физическому смыслу коэффициент теплоотдачи есть плотность теплового потока (q) на поверхности тела, отнесенная к разности температур поверхности тела и окружающей среды. Коэффициент теплоотдачи численно равен плотности теплового потока при температурном напоре, равном единице.
Коэффициент теплоотдачи зависит от многих факторов. В наиболее общем случае является функцией формы и размера тела, режима движения жидкости, физических свойств жидкости, положения в пространстве и состояние поверхности теплообмена и других величин. Процесс теплоотдачи в зависимости от природы движения жидкости протекает различно.
Вопрос №36
Лучистый теплообмен.
Твёрдые тела излучают и поглощают энергию во всём диапазоне длин волн поверхностным слоем. Интенсивность излучения зависит только от температуры. Жидкости ведут себя аналогичным образом. Газы излучают и поглощают энергию в ограниченном диапазоне длин волн всем объёмом. Интенсивность излучения газов зависит от температуры, толщины слоя и парциального давления компонентов.
Лучистая энергия 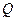 - энергия, излучаемая телом во всём диапазоне длин волн,
- энергия, излучаемая телом во всём диапазоне длин волн, 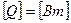 .
.
Интенсивность излучения 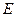 – количество энергии, излучаемой с единицы поверхности,
– количество энергии, излучаемой с единицы поверхности, 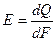 .
.
Лучистую энергию можно найти по формуле: 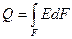 .
.
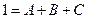 , где
, где 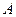 - коэффициент отражения,
- коэффициент отражения, 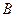 - коэффициент поглощения,
- коэффициент поглощения, 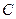 - коэффициент прозрачности.
- коэффициент прозрачности.
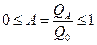 ,
, 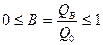 ,
, 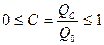 .
.
Если 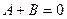 , то есть
, то есть 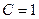 ,то тело называется абсолютно белым.
,то тело называется абсолютно белым.
Если 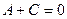 , то есть
, то есть 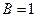 , то тело называется абсолютно чёрным.
, то тело называется абсолютно чёрным.
Плотность интегрального излучения, отнесенная к рассматриваемому диапазону длин волн, называется спектральной интенсивностью излучения 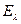 (Вт/м3):
(Вт/м3):
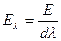 .
.
Угловая интенсивность: 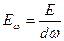 .
.
Спектральная угловая интенсивность: 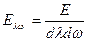 .
.
Закон Планка устанавливает зависимость интенсивности излучения абсолютно черного тела E0λ от длины волны λ и температуры Т

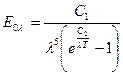
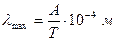 , где
, где 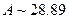 .
.
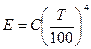
Степень черноты: 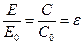 .
.
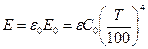 .
.
3акон Кирхгофа формулируется так: отношение плотности полусферического интегрального излучения к поглощательной способности одинаково для всех тел имеющих одинаковую температуру и равно плотности интегрального полусферического излучения абсолютно черного тела при той же температуре: 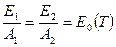 , где
, где 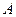 - коэффициент поглощения.
- коэффициент поглощения.
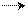
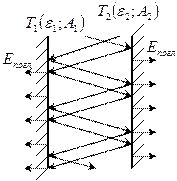
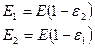
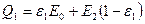
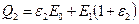
Количество теплоты, которое останется у одного из двух тел: 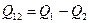 .
.
Закон смещения Вина гласит – длина волны, которой соответствует максимальное значение интенсивности излучения (E0λ=max), обратно пропорциональна абсолютной температуре рис.11

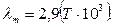 ,
,
Вопрос №37
Теплообмен излучением между твердыми телами.
На основании законов излучения получено расчетное уравнение лучистого теплообмена между телом 1 произвольной формы и поверхностью другого, большего и охватывающего его тела 2 (рис. 14)
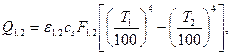
где Q1,2 – тепловой поток, передаваемый излучением телом 1 телу 2, Вт;
ε1,2 – приведенная степень черноты тел 1 и 2, определяемая из выражения
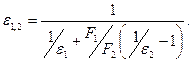
F1 и F2 – площади поверхностей тел 1 и 2, м2; Т 1 и Т2 — абсолютная температура поверхностей тел 1 и 2, К.
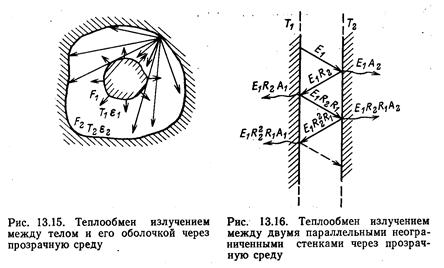
Такой случай еще называют теплообменом излучением между телом и его оболочкой; внутреннее тело всегда тело 1.
Частный случай рассмотренного теплообмена — теплообмен между двумя параллельными неограниченными стенками (рис. 15). Когда F1 = F2 = F, применяют расчетное уравнение теплообмена излучением, а приведенная степень черноты определяется из выражения
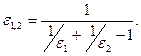
Уравнение (2.57)можно использовать для расчета лучистого теплообмена между двумя телами любой формы и произвольного их расположения, только в каждом частном случае для определения приведенных степени черноты и поверхности (для ε1,2 и F1,2) имеются свои расчетные выражения.
Вопрос №38
Теплопередача чрез плоскую однослойную и многослойную
плоскую стенку
Уравнение теплопроводности: 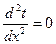 .
. 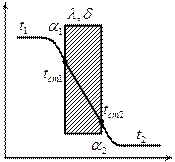
Граничные условия первого рода: 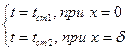 .
.
Граничные условия третьего рода: 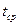 ,
, 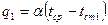 .
.
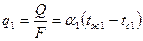 ;
; 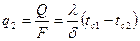 ;
; 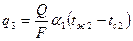
В этом ряду равенств первое уравнение определяет количество теплоты, передаваемой конвекцией (и излучением) от горячего теплоносителя к стенке; второе уравнение – то же количество теплоты, передаваемой теплопроводностью через стенку; третье уравнение – передачу того же самого количества теплоты, передаваемого конвекцией (и излучением) от стенки к холодному теплоносителю.
Выделим из этого ряда равенств разности температур
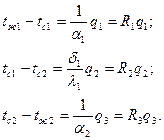
Складывая левые и правые части уравнений характеризующих разности температур и учитывая, что 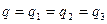 получим выражение для итоговой разности температур
получим выражение для итоговой разности температур
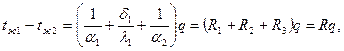
где 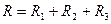 –термическое сопротивление плоской стенки (м2 0С\Bm)
–термическое сопротивление плоской стенки (м2 0С\Bm)
Отсюда, следует выражение для плотности теплового потока и теплового потока (уравнение теплопередачи плоской стенки)
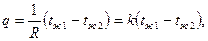
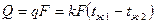 ,
,
где q – плотность теплового потока (Вт/м2 );
Q – тепловой поток (Вт);
k=1/R – коэффициентом теплопередачи плоской стенки (Вт/м2 ºС)
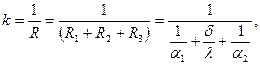
где 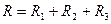 —термическое сопротивление теплопередачи плоской стенки (м2 ºС/Вт);
—термическое сопротивление теплопередачи плоской стенки (м2 ºС/Вт);
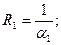
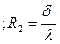 ;
; 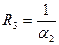 - термические сопротивления теплоотдачи со стороны горячего теплоносителя, теплопроводности плоской стенки и термические сопротивления теплоотдачи со стороны холодного теплоносителясоответственно.
- термические сопротивления теплоотдачи со стороны горячего теплоносителя, теплопроводности плоской стенки и термические сопротивления теплоотдачи со стороны холодного теплоносителясоответственно.
Температура внутренней и наружной поверхности стенки определяется из следующих соображений:
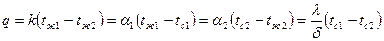 ,
,
отсюда имеем
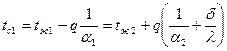 ,
, 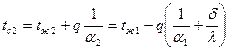
В случае многослойной стенки
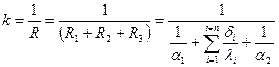
Вопрос № 39
Теплопередача – передача теплоты от одного носителя к другому через разделяющую их твёрдую поверхность.
Стационарный процесс – процесс, при котором температуры сред не меняются, то есть 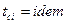 .
.
Нестационарный процесс – процесс, при котором температуры сред меняются, то есть 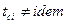 .
.
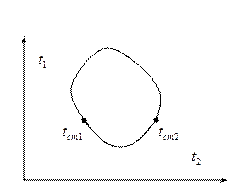
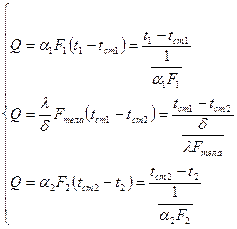
Для криволинейных стенок коэффициент теплопередачи принято определять по тому же уравнению, что и для плоской стенки 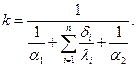 В этом случае для криволинейных стенок расчетная поверхность теплопередачи определяется из выражения
В этом случае для криволинейных стенок расчетная поверхность теплопередачи определяется из выражения
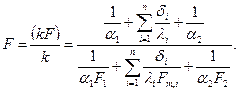
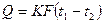
Водяной эквивалент поверхности теплопередачи 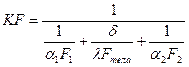 .
.
Для цилиндрических стенок: 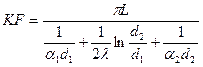 .
.
Линейный коэффициент теплопередачи: 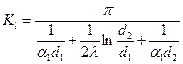 .
.
Коэффициент теплопередачи для внутренней стенки: 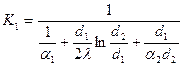 .
.
Коэффициент теплопередачи для внешней стенки: 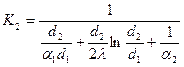 .
.
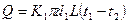 .
.
Вопрос №40-41
Классификация теплообменных аппаратов.
1. По типу действия:
a. Аппараты поверхностного типа – аппараты, в которых передача теплоты идёт при наличии твёрдой поверхности.
i. Регенеративные аппараты – аппараты поверхностного типа, в которых твёрдая поверхность попеременно омывается горячим и холодным теплоносителями. Эти аппараты используются в случаях, когда теплоносители обладают высокими температурами, или когда теплоносители не являются чистыми.
ii. Рекуперативные аппараты – аппараты поверхностного типа, в которых твёрдая поверхность омывается непрерывно горячим и тёплым теплоносителями через разделяющиеся поверхности.
1. Кожухо-трубные теплообменные аппараты.
2. Аппараты типа «труба в трубе»:
a. Однопоточные аппараты типа «труба в трубе».
b. Многопоточные аппараты типа «труба в трубе».
b. Аппараты смесительного типа – аппараты, в которых идёт непосредственное перемешивание горячих и холодных теплоносителей.
Схема аппарата типа «труба в трубе»:
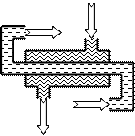 Аппараты такого типа имеют простую конструкцию и высокие скорости потока, однако, для получения больших мощностей аппарата требуется установка большого количества элементов конструкции и сам аппарат будет занимать много места.
Аппараты такого типа имеют простую конструкцию и высокие скорости потока, однако, для получения больших мощностей аппарата требуется установка большого количества элементов конструкции и сам аппарат будет занимать много места.
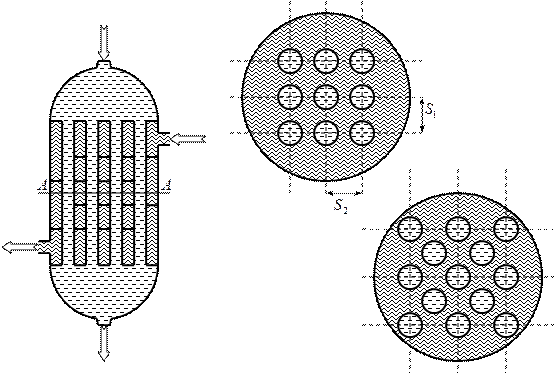
Схема аппарата кожухо-трубчатого типа:
В таких аппаратах возможно создание прямоточных, противоточных, перекрёстноточных, U-образных симметричных и других потоков.
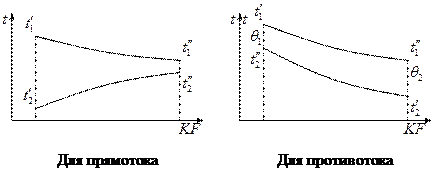
Тепловой баланс теплообменного аппарата: 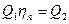 , где
, где 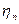 - коэффициент эффективности теплового аппарата,
- коэффициент эффективности теплового аппарата, 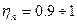 .
.
1. 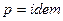 (гидравлическое сопротивление мало), тогда
(гидравлическое сопротивление мало), тогда 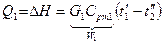 ,
, 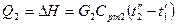 ,
, 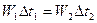 , при
, при 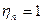 .
.
2. Конденсатор. 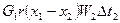
3. Испаритель. 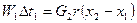
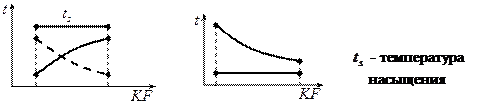
Мощность теплового аппарата (уравнение Гросгофа): 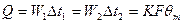 , где
, где 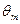 - средняя разность температур.
- средняя разность температур.
Для прямотока: 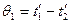 ,
, 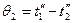 .
.
Для противотока: 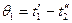 ,
, 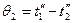 .
.
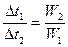 , где
, где 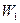 и
и 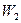 - водяные эквиваленты поверхности теплообмена.
- водяные эквиваленты поверхности теплообмена.
Для любой схемы 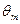 может быть определено в соответствие с двумя методиками:
может быть определено в соответствие с двумя методиками:
1. Классическая методика: 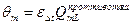 , где
, где 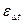 - коэффициент, зависящий от типа и свойств теплого аппарата, определяется по графикам функций
- коэффициент, зависящий от типа и свойств теплого аппарата, определяется по графикам функций 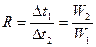 и
и 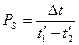 .
.
2. Метод Белоконя. Индекс противоточности:
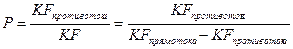 .
.
Для прямотока 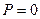 .
.
Для противотока 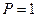 .
.
Для U-образной симметричной схемы 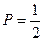 .
.
Для любой схемы средняя разность температур: 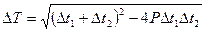 .
.
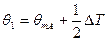
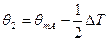
Вопрос №42
Различают два типа расчётов тепловых аппаратов:
1. Расчёт первого рода (конструктивный). Известно: 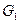 ,
, 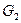 ,
, 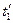 ,
, 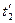 ,
, 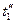 ,
, 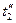 ,
, 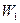 ,
, 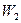 . Задача: Выбор или конструирование теплообменного аппарата (
. Задача: Выбор или конструирование теплообменного аппарата (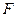 ,
, 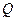 ).
).
a. Находим мощность: 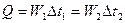 .
.
b. Находим среднюю разность температур 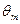 .
.
c. 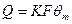 , следовательно,
, следовательно, 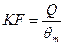 .
.
d. 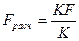 , где
, где 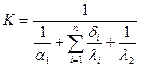 .
.
e. Находим проходные сечения по трубному и межтрубному пучку 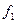 и
и 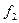 :
: 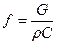 , где
, где 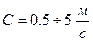 для жидкости и
для жидкости и 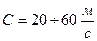 для газа.
для газа.
Вопрос №43
Расчёт второго рода. Известно: 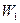 ,
, 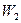 ,
, 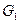 ,
, 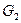 ,
, 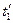 ,
, 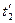 ,
, 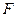 ,
, 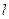 . Найти:
. Найти: 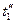 ,
, 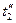 ,
, 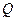 .
.
Проверка расчётов второго рода.
Дано: геометрия, 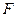 ,
, 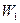 ,
, 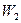 ,
, 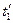 ,
, 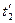 ,
, 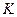 (из расчётов первого рода).
(из расчётов первого рода).
Найти: 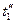 и
и 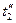 .
.
Решение:
В случае если 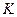 не дано, то его модно найти по формуле:
не дано, то его модно найти по формуле: 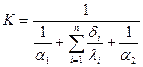 . Из логических соображений зададимся температурами
. Из логических соображений зададимся температурами 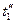 и
и 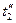 , тогда
, тогда 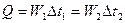 , где
, где 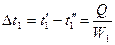 ,
, 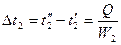 . Используя метод Белоконя, получим следующее уравнение:
. Используя метод Белоконя, получим следующее уравнение: 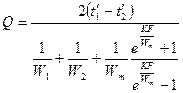 , тогда
, тогда 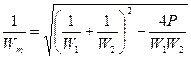
Вопрос №44
Паросиловые установки (циклы):
a. Объекты, производящие тепловую энергию.
b. Объекты, производящие работу.
Цикл Карно (рабочее тело – конденсирующий газ).
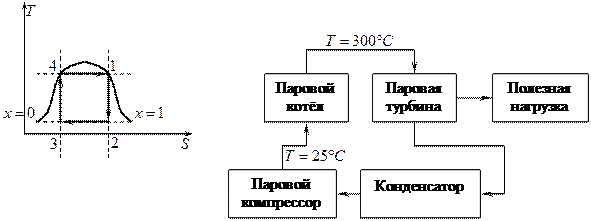
Паровые котлы бывают двух типов: прямоточного типа и барабанного типа.
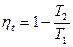
Удельная работа в турбине 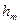 .
.
Удельная работа в компрессоре 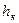 .
.
Полезная удельная работа 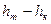 .
.
Эффективный коэффициент полезного действия системы: 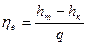 .
.
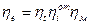 , где
, где 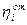 - относительный индикаторный коэффициент полезного действия,
- относительный индикаторный коэффициент полезного действия, 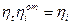 - индикаторный внутренний коэффициент полезного действия,
- индикаторный внутренний коэффициент полезного действия, 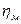 - механический коэффициент полезного действия.
- механический коэффициент полезного действия.
Цикл Ренкина – идеальный цикл для паросильных установок.
Вместо компрессора устанавливают насос и пароперегреватель.
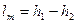
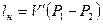 , где
, где 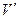 - объём жидкости.
- объём жидкости.
Пренебрегая работой насоса, получим: 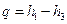
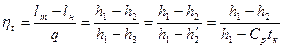
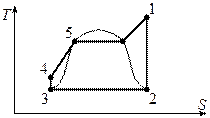 , где
, где 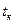 - температура конденсации.
- температура конденсации.
Для увеличения эффективности надо одновременно увеличивать давление и температуры перегрева.
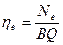 , где
, где 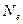 - эффективная мощность турбины,
- эффективная мощность турбины, 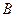 - расход топлива,
- расход топлива, 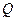 - теплотворная способность.
- теплотворная способность.
Вопрос №45
Холодильные установки предназначены для охлаждения тел до температуры ниже температуры окружающей среды. Чтобы осуществить такой процесс, необходимо от тела отвести теплоту и передать ее в окружающую среду за счет работы, подводимой извне.
Цикл Карно:
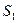
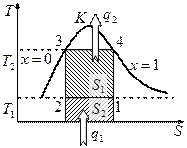 - работа цикла.
- работа цикла.
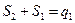 ;
;
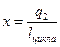 ;
;
Холодильные машины бывают следующих видов:
1. Парокомпрессионные холодильные машины, в которых рабочим телом является пар, а рабочий процесс протекает в компрессоре.
2. Воздушные холодильные машины, в которых рабочим телом является воздух.
3. Абсорбционные холодильные машины, в которых идёт поглощение паров водными растворами.
4. Пароструйные холодильные машины, имеющие инжекторы в качестве исполнительного механизма.
Рабочий процесс парокомпрессионной холодильной установки:
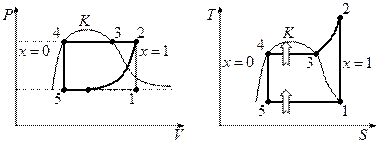 1-2 – адиабатическое сжатие; 4-5 – процесс дросселирования.
1-2 – адиабатическое сжатие; 4-5 – процесс дросселирования.
Схема парокомпрессионной холодильной установки:
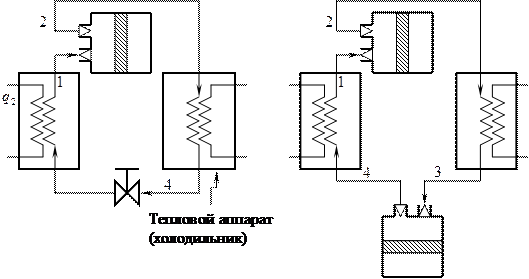
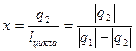 ;
;
Такие установки работают в следующем интервале температур: 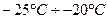 .
.
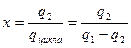 ; Так как воздух можно считать идеальным газом, то
; Так как воздух можно считать идеальным газом, то 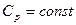 .
.
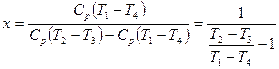 ;
; 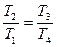 .
.
Вопрос №46
Холодильные установки предназначены для охлаждения тел до температуры ниже температуры окружающей среды. Чтобы осуществить такой процесс, необходимо от тела отвести теплоту и передать ее в окружающую среду за счет работы, подводимой извне.
Цикл Карно:
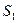
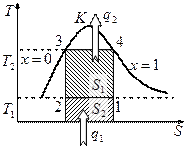 - работа цикла.
- работа цикла.
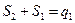 ;
;
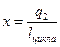 ;
;
Холодильные машины бывают следующих видов:
5. Парокомпрессионные холодильные машины, в которых рабочим телом является пар, а рабочий процесс протекает в компрессоре.
6. Воздушные холодильные машины, в которых рабочим телом является воздух.
7. Абсорбционные холодильные машины, в которых идёт поглощение паров водными растворами.
8. Пароструйные холодильные машины, имеющие инжекторы в качестве исполнительного механизма.
 2015-04-20
2015-04-20 5115
5115

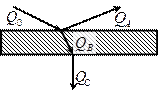
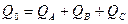 .
.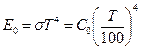 .
.