Динамические эконометрические модели (ДЭМ). Общая характеристика. Модели авторегрессии. Интерпретация параметров

К динамическим эконометрическим моделям (ДЭМ) относят модели, которые в данный момент времени учитывают значения входящих в нее переменных, относящихся к текущему и к предыдущему моментам времени. Например, 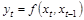; 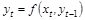– ДЭМ, а 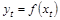– не ДЭМ.

Выделяют 2 типа динамических эконометрических моделей ДЭМ:

1. Модели, в которых лаговые значения переменных (переменных, относящихся к предыдущим моментам времени) непосредственно включены в модель. Это модели авторегрессии и модели с распределенным лагом.

Модели авторегрессии – это ДЭМ, в которых в качестве факторных переменных содержатся лаговые значения результативной переменной. Например, .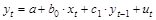

Модели с распределенным лагом – это ДЭМ, в которых содержатся не только текущие, но и лаговые значения факторных переменных. Например, .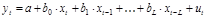

2. Модели, в которых включены переменные, характеризующие ожидаемый или желаемый уровень признака-результата или одного из факторов в момент времени t. Этот уровень считается неизвестным и определяется с учетом информации, которой располагают в предыдущий момент времени t – 1.

Ожидаемые значения показателей определяют различными способами. В зависимости от способа различают модели:

• неполной корректировки;

• адаптивных ожиданий;

• рациональных ожиданий.

Оценка параметров этих моделей сводится к оценке параметров моделей авторегрессии.

Модели авторегрессии. Модели авторегрессии – это ДЭМ, в которых в качестве факторных переменных содержатся лаговые значения результативной переменной. Например, .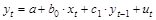

Коэффициент регрессии b₀ в данной модели характеризует краткосрочное изменение у под влиянием изменения x на единицу своего измерения.

Коэффициент с₁ характеризует изменение у в момент t под воздействием своего изменения в предшествующий момент времени (t – 1).

Произведение коэффициентов (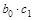) – называют промежуточным мультипликатором. Данный показатель характеризует общее абсолютное изменение результата у в момент (t + 1).

Показатель 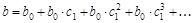– называют долгосрочным мультипликатором. Он характеризует общее абсолютное изменение у в долгосрочном периоде.

Практически во все модели авторегрессии вводят условие стабильности, состоящее в том, что 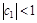. Тогда при наличии бесконечного лага:

.

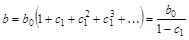Применение МНК к моделям авторегрессии неприемлемо, т. к. нарушается 1-я предпосылка нормальной линейной модели регрессии, а именно, одна из объясняющих переменных (y_t-1) частично зависит от случайной составляющей (u_t). Это приводит к получению смещенной оценки параметра при переменной y_t-1.