2015-05-10
2335
Предполагается, что объясняемая переменная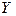 
зависит от двух факторов 
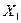и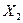 
, поэтому уравнение регрессии будем искать в виде:
,
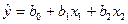1. В главном меню выбрать последовательно пункты: Сервис – Анализ данных – Регрессия
2. Заполнить диалоговое окно инструмента Пакета анализа Регрессия
Входные данные:
Входной интервал 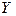– диапазон (столбец или строка), содержащий данные результативного признака. – Необходимо выделить столбец с признаком 
.
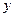Входной интервал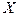 
– диапазон, содержащий данные факторов независимых признаков (одновременно выделяются столбцы, содержащие значения факторных признаков 
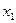и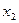 
)
Метки (да или нет) – флажок, который указывает, содержит ли первая строка названия столбцов или нет.
Введите название листа, в котором будут выведены результаты расчета, заполнив поле Новый рабочий лист.
Нажмите ОК. На отдельном листе появятся итогирегрессионного анализа, содержащие 3 таблицы:
Регрессионная статистика
Таблица без названия
3. Параметры (коэффициенты) уравнения регрессии находятся в таблице без названия. Запишите линейное уравнение регрессии в бланк отчета.
4. Из таблицы «Регрессионная статистика» выпишите в бланк отчета значения индекс множественной корреляции, индекс множественной детерминации и скорректированный коэффициент детерминации.
5. Найдите матрицу парных коэффициентов корреляции с помощью EXCEL. В главном меню выбрать последовательно пункты: Сервис – Анализ данных – Корреляция. Заполнить диалоговое окно ввода данных и параметров вывода: Входной интервал – следует указать все столбцы, содержащие значения результативного и факторных признаков. Выходной интервал – достаточно указать левую верхнюю ячейку будущей матрицы. Нажмите ОК.
6. Выпишите значения коэффициентов парной корреляции и сделайте выводы о характере связи между результативным признаком 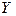с каждым из действующих факторов 
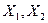и характере межфакторной связи.
7. Оцените статистическую значимость уравнения в целом. Для оценки качества уравнения регрессии в целом необходимо проверить значимость индекса детерминации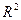 
: проверяется нулевая гипотеза 
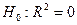, используется 
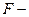критерий.
7.1 Наблюдаемое значение критерия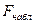 
можно взять из таблицы Дисперсионный анализ.
7.2. Найдите табличное значение критерия Фишера. Выделите клетку, в которой должно появиться значение 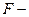критерия. В главном меню выберите Вставка/функция. В окне Категория выберите Статистические, затем в окне Функция – FРАСПОБР. Заполните диалоговое окно. Щелкните по кнопке ОК. Появится табличное значение критерия Фишера.
7.3. Сравните критическое значение 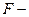критерия с наблюдаемым значением. Сделайте вывод.
8. Для статистической оценки значимости коэффициентов регрессии (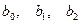
) используем 
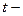статистику Стьюдента. Проверяется нулевая гипотеза 
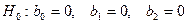. Наблюдаемые значения критерия Стьюдента 
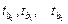можно найти в Таблице без названия.
8.1. Найдите критическое значение коэффициента Стьюдента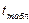 
. Выделите клетку, в которой вы хотите разместить значение 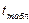. Выполните последовательно процедуры: Вставка-функция - статистические-СТЬЮДРАСПОБР. Введите значения уровня значимости 
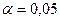и числа степеней свободы 
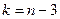. Нажмите ОК.
8.2. Сравните 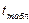с наблюдаемыми значениями критерия Стьюдента. Сделайте вывод о статистической значимости параметров уравнения регрессии.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Понятие уравнения множественной регрессии. Приведите примеры.
2. Каким необходимо следовать правилам при отборе факторов в уравнение регрессии.
3. Степенное и линейное уравнение множественной регрессии. Экономический смысл коэффициентов.
4. Матрица парных коэффициентов корреляции. Понятие мультиколлинеарности. Анализ матрицы парных коэффициентов корреляции на наличие мультиколлинеарности.
5. Перечислите недостатки МНК-оценок при наличии мультиколлинеарности.
6. Методы устранения мультиколлинеарности.
7. Индекс множественной корреляции. Скорректированный индекс множественной регрессии.
8. Проверка статистической значимости параметров множественного линейного уравнения регрессии, а также уравнения в целом.
