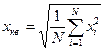 – среднее квадратичное.
– среднее квадратичное.
· Величина может принимать только дискретные значения.
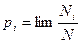 при N → ∞ – вероятность того, что величина x принимает значение х i, здесь N – полное число измерений, N i – число опытов, в которых величина x принимает значение х i;
при N → ∞ – вероятность того, что величина x принимает значение х i, здесь N – полное число измерений, N i – число опытов, в которых величина x принимает значение х i;
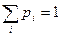 – условие нормировки;
– условие нормировки;
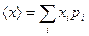 – среднее значение величины х, где р i – вероятность того, что величина x принимает значение х i;
– среднее значение величины х, где р i – вероятность того, что величина x принимает значение х i;
pi или j = pi + pj – закон сложения вероятностей, здесь pi или j – вероятность получить результат xi или xj;
p (xi, yj)= p (xi) p (yj) – закон умножения вероятностей, где p (xi, yj) – вероятность появления xi одновременно с yj, причем значение y не зависит от x;
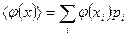 – среднее значение любой функции φ (x);
– среднее значение любой функции φ (x);
· Величина принимает непрерывный ряд значений.
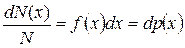 – вероятность того, что результат измерения лежит в интервале (x; x+dx), здесь f (x) – функция распределения, N – полное число измерений; dN (x) – число измерений, при которых результат измерения лежит в интервале (x; x+dx);
– вероятность того, что результат измерения лежит в интервале (x; x+dx), здесь f (x) – функция распределения, N – полное число измерений; dN (x) – число измерений, при которых результат измерения лежит в интервале (x; x+dx);

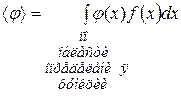 – среднее значение любой функции φ (x); здесь f (x) – функция распределения;
– среднее значение любой функции φ (x); здесь f (x) – функция распределения;
|
|
|
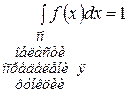 – условие нормировки функции распределения.
– условие нормировки функции распределения.
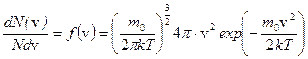 – функция распределения Максвелла молекул по скоростям (доля молекул, имеющих скорости в интервале от v до v+dv вблизи заданной скорости v, в расчете на единичный интервал скоростей);
– функция распределения Максвелла молекул по скоростям (доля молекул, имеющих скорости в интервале от v до v+dv вблизи заданной скорости v, в расчете на единичный интервал скоростей);
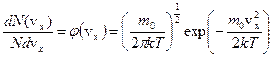 – функция распределения Максвелла молекул по компоненте скорости (доля молекул, имеющих проекцию vx скорости на ось OX в интервале от vx до vx+dvx вблизи заданного значения vx, в расчете на единичный интервал проекции скорости);
– функция распределения Максвелла молекул по компоненте скорости (доля молекул, имеющих проекцию vx скорости на ось OX в интервале от vx до vx+dvx вблизи заданного значения vx, в расчете на единичный интервал проекции скорости);
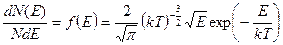 – функция распределения Максвелла молекул по энергиям (доля молекул, имеющих энергию в интервале от Е до Е + dЕ вблизи заданного значения Е, в расчете на единичный интервал энергий);
– функция распределения Максвелла молекул по энергиям (доля молекул, имеющих энергию в интервале от Е до Е + dЕ вблизи заданного значения Е, в расчете на единичный интервал энергий);
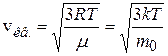 ;
; 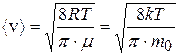 ;
; 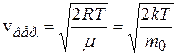 – скорости молекул газа: средняя квадратичная, средняя арифметическая, наиболее вероятная;
– скорости молекул газа: средняя квадратичная, средняя арифметическая, наиболее вероятная;
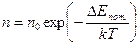 – распределение Больцмана, здесь n и n0 – концентрации частиц в состояниях с потенциальными энергиями Е и Е 0 соответственно, Δ Е пот.= Е – Е 0;
– распределение Больцмана, здесь n и n0 – концентрации частиц в состояниях с потенциальными энергиями Е и Е 0 соответственно, Δ Е пот.= Е – Е 0;
 2015-05-13
2015-05-13 1721
1721

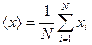 –
– 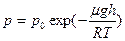 ,
, 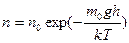 –
–