1. Статистическое определение вероятности.
Пусть некоторый эксперимент повторяется 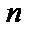 раз (т.е. проводится серия из
раз (т.е. проводится серия из 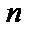 одинаковых и независимых друг от друга экспериментов). Фиксируем случайное событие
одинаковых и независимых друг от друга экспериментов). Фиксируем случайное событие 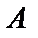 и предполагаем, что это событие появилось
и предполагаем, что это событие появилось 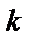 раз. Рассмотрим отношение
раз. Рассмотрим отношение 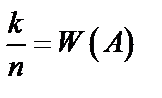 , которое называется частотой события
, которое называется частотой события 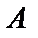 в данной серии. С ростом
в данной серии. С ростом 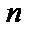 колебание этого отношения вокруг некоторого постоянного числа
колебание этого отношения вокруг некоторого постоянного числа 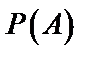 все меньше и в различных сериях практически совпадают при больших
все меньше и в различных сериях практически совпадают при больших 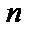 , т.е.
, т.е. 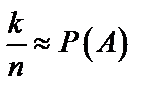 .
.
Итак, событию 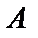 сопоставляется численная характеристика
сопоставляется численная характеристика 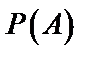 , которая и называется вероятностью события
, которая и называется вероятностью события 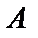 . Такую трактовку понятия вероятности называют частотным или статистическим определением вероятности.
. Такую трактовку понятия вероятности называют частотным или статистическим определением вероятности.
Частота 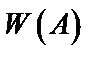 обладает следующими свойствами:
обладает следующими свойствами:

2. Классическое определение вероятности.
Определение. События 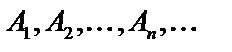 образуют полную систему (или группу) событий, если
образуют полную систему (или группу) событий, если
1) 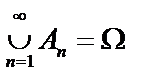 ;
;
2) 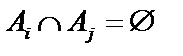 , при
, при 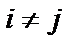 .
.
Пусть 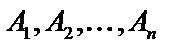 образуют полную систему событий. Рассмотрим событие
образуют полную систему событий. Рассмотрим событие 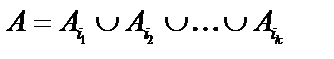 , тогда будем говорить, что событию
, тогда будем говорить, что событию 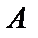 благоприятствуют
благоприятствуют 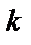 из
из 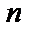 событий
событий 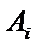 .
.
Теорема. Пусть 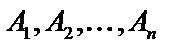 образуют полную систему событий и равновозможны, и пусть событию
образуют полную систему событий и равновозможны, и пусть событию 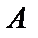 благоприятствуют
благоприятствуют 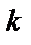 из
из 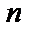 событий, тогда
событий, тогда 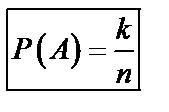 (59)
(59)
Пример. В урне имеются 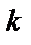 белых и
белых и 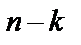 красных шаров. Извлекается из урны 1 шар. Какова вероятность того, что этот шар белый?
красных шаров. Извлекается из урны 1 шар. Какова вероятность того, что этот шар белый?
Все исходы равновозможны, их всего 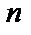 :
: 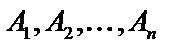 . Событию
. Событию 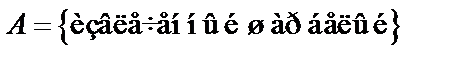 благоприятствует
благоприятствует 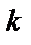 из
из 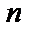 исходов, поэтому из теоремы следует ответ:
исходов, поэтому из теоремы следует ответ: 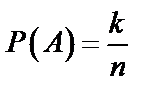 .
.
 2015-05-13
2015-05-13 343
343








