П р и м е р 1. Построить отрицание для следующих высказываний и определить их истинностное значение:
a) 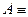 «11>0»;
«11>0»;
б) 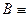 «7 делится на 3»;
«7 делится на 3»;
в) 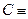 «3+4=7».
«3+4=7».
Решение. a) отрицанием истинного высказывания 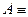 ”11>0» является ложное высказыванием
”11>0» является ложное высказыванием 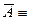 «11
«11 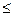 0».
0».
б) отрицанием ложного высказывания 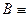 «7 делится на 3» будет истинное высказывание
«7 делится на 3» будет истинное высказывание 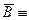 «7 не делится на 3».
«7 не делится на 3».
в) 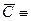 «3+4
«3+4  7» ложное высказывание.
7» ложное высказывание.
П р и м е р 2. Записать символически высказывание «15 делится на 3 и на 5».
Решение. Это высказывание есть конъюнкция двух высказываний 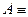 «15 делится на 3» и
«15 делится на 3» и 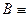 «15 делится на 5». Поэтому получим:
«15 делится на 5». Поэтому получим: 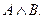
П р и м е р 3. Прочитать по правилам русского языка символически записанное высказывание 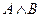 , если
, если 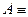 «2 – простое число»,
«2 – простое число», 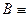 «2 – четное число».
«2 – четное число».
Ответ: «2 – простое и четное число».
П р и м е р 4. Пусть 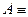 «Иван умен»,
«Иван умен», 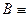 «Петр умен»
«Петр умен»
Записать символически:
a) Иван умен и Петр глуп;
б) Иван и Петр оба глупы;
в) или Иван умен или Петр глуп;
г) если Иван умен, то Петр глуп.
Решение.
a) 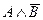
б) 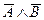
в) 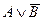
г) 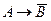 .
.
П р и м е р 5. Пусть 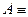 «У меня есть собака»,
«У меня есть собака», 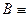 «У меня есть кошка”. Перевести на разговорный язык:
«У меня есть кошка”. Перевести на разговорный язык:
a) 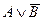 ;
;
б) 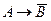 ;
;
в) 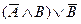 ;
;
г) 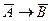 .
.
Решение. a)У меня есть собака или у меня нет кошки;
б) Если у меня есть собака, то у меня нет кошки;
в) Или у меня нет собаки и есть кошка, или у меня нет кошки;
г) Если у меня нет собаки, то у меня нет кошки.
П р и м е р 6. Какие из данных высказываний истинны?
a) 3 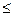 5;
5;
б) 7 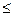 7;
7;
в) 3 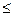 0.
0.
Решение. a) имеем дизъюнкцию: 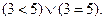 Так как первый член дизъюнкции истинный, то и вся дизъюнкция истинна.
Так как первый член дизъюнкции истинный, то и вся дизъюнкция истинна.
б) высказывание «7 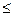 7» истинно, так как «7=7» истинно.
7» истинно, так как «7=7» истинно.
в) «3 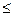 0» ложно, т.к. оба члена дизъюнкции ложны.
0» ложно, т.к. оба члена дизъюнкции ложны.
П р и м е р 7. Постройте импликацию высказывания «25 при делении на 7 дает остаток 2» и «11>0» и определите ее истинностное значение.
Решение. «Если 25 при делении на 7 дает остаток 2, то 11>0» – истинное высказывание, поскольку истинно его заключение.
П р и м е р 8. Постройте эквиваленцию высказываний «25 при делении на 7 дает остаток 2» и «2 является конем уравнения 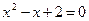 », и определите ее истинное значение.
», и определите ее истинное значение.
Решение. «25 при делении на 7 дает остаток 2 тогда и только тогда, когда 2 является конем уравнения 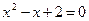 ». Это высказывание истинно, как эквиваленция ложных высказываний.
». Это высказывание истинно, как эквиваленция ложных высказываний.
П р и м е р 9.Какие из данных высказываний истинны:
a) 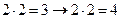 ;
;
б) 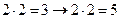 ;
;
в) 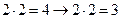 ;
;
г) 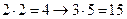 ;
;
д) 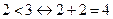 ;
;
е) 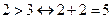 ;
;
ж) 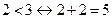 ;
;
з) 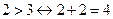 .
.
Ответ: а), б), г), д), е) – истинны;
в), ж), з) – ложны.
П р и м е р 10. Построить таблицы истинности для следующих формул:
a) 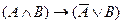 ;
;
б) 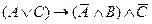 ;
;
в) 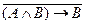 ;
;
г) 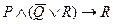 .
.
Определить является ли каждая из формул тавтологией, противоречием или выполнимой.
Решение. Для сложной формулы F можно предложить следующий порядок заполнения таблицы истинности:
1.В строку выписываются сначала все атомы, а затем все подформулы F (не считая атомов), начиная с простых и кончая самой формулой F. Для каждой записи подготавливается столбец.
2.Атомам формулы F даются всевозможные наборы значений из множества {1;0}, компоненты которых записываются в соответствующие столбцы. Можно показать, что различных наборов значений истинности атомов (значит и строк таблицы) будет всего 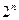 , где n – число атомов формулы F. Для удобства значения располагают так: под первым атомом подряд пишут половину (т.е.
, где n – число атомов формулы F. Для удобства значения располагают так: под первым атомом подряд пишут половину (т.е. 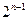 ) значений 1, затем столько же значений 0; под вторым атомом пишут подряд четвертую часть (т.е.
) значений 1, затем столько же значений 0; под вторым атомом пишут подряд четвертую часть (т.е. 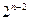 ) значений 1, затем столько же значений 0, повторяют это еще раз и т.д. Под последним атомом значений 1 и 0 чередуются.
) значений 1, затем столько же значений 0, повторяют это еще раз и т.д. Под последним атомом значений 1 и 0 чередуются.
3.Столбцы всех подформул формулы F и столбец самой формулы F заполняются согласно определениям соответствующих операций.
а) так как формула имеет две переменные, ее таблица истинности содержит четыре строки 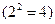 .
.
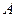 | 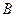 | 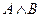 | 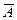 | 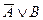 | 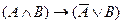 |
Так как последний столбец таблицы содержит только значения 1, то формула 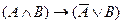 является тавтологией.
является тавтологией.
Заметим, что 3, 4, 5 столбцы являются вспомогательными и в таблице истинности могут отсутствовать.
б) Поскольку формула содержит три высказывательные переменные, то ее таблица истинности содержит восемь строк 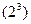 .
.
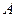 | 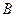 | 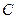 | 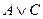 | 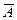 | 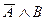 | 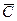 | 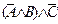 | 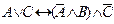 |
Эта формула является одновременно выполнимой и опровержимой, так как на наборе значений переменных 0, 0, 0 формула принимает значение 1, а на остальных наборах формула принимает значение 0.
в)
 |  | 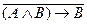 |
В этой таблице не приведен вспомогательный столбец. Формула является противоречием.
г)
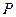 | 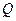 | 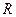 | 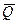 | 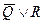 | 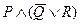 | 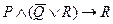 |
В построенной таблице не заполнены вспомогательные столбцы (сделайте это самостоятельно). Формула является одновременно выполнимой и опровержимой.
П р и м е р 11. Проверить являются ли следующие формулы равносильными:
a) 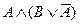 и
и 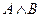 ;
;
б) 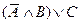 и
и 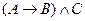 .
.
Решение.
а) составим таблицы истинности для данных формул (их удобно совместить). Получим:
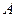 | 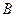 | 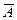 | 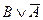 | 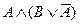 | 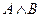 |
Сравнивая два последних столбца, мы видим, что они одинаковые. Значит, формулы равносильны (или логически равны): 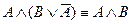 .
.
б) составим таблицы истинности:
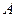 | 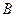 | 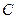 | 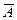 | 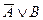 | 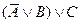 |  | 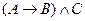 |
Сравнивая 6-й и 8-й столбцы таблицы, видим, истинностные значения формул различаются при значениях переменных 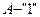 ,
, 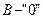 ,
, 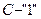 . Следовательно, эти формулы не являются равносильными.
. Следовательно, эти формулы не являются равносильными.
П р и м е р 12. Упросить формулы, применяя основные равносильности алгебры высказываний (стр. 32 учебного пособия Л.М.Мартынова).
а) 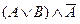 ;
;
б) 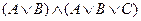 ;
;
в) 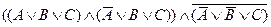 ;
;
г) 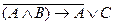 .
.
Решение.
а) 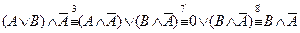 (здесь применили дистрибутивный закон, закон противоречия 7’ и свойство 0 – 8’).
(здесь применили дистрибутивный закон, закон противоречия 7’ и свойство 0 – 8’).
б) 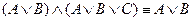 , т.к. если обозначить
, т.к. если обозначить 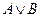 через Х, то получим
через Х, то получим 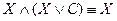 по закону поглощения 4.
по закону поглощения 4.
в) 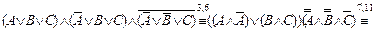
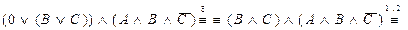
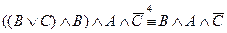 .
.
г) 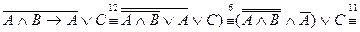
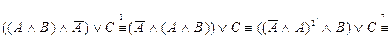
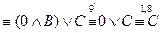 .
.
П р и м е р 13. Записать формулу 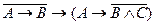 с помощью только конъюнкции и отрицания.
с помощью только конъюнкции и отрицания.
Решение. 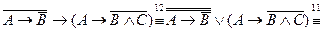
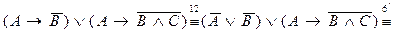
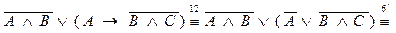
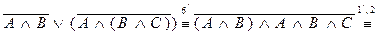
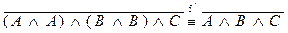 .
.
П р и м е р 14. Доказать, что формула 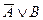 есть логическое следствие формул
есть логическое следствие формул 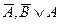 .
.
Решение. 1-й способ. Докажем, что 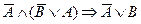 по определению. Для этого составим всевозможные наборы истинностных значений для высказывательных переменных
по определению. Для этого составим всевозможные наборы истинностных значений для высказывательных переменных 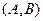 , вычислим для них соответствующие значения посылки
, вычислим для них соответствующие значения посылки 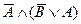 и значения
и значения 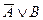 и сравним только те значения этих формул, при которых посылка истинна.
и сравним только те значения этих формул, при которых посылка истинна.
Легко понять, что первая формула принимает значение 1 лишь для набора истинностных значений 0,0. Требуемое логическое следование вытекает из фрагмента таблицы истинности
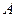 | 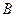 | 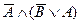 | 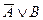 |
2-й способ. По признаку логического следования для высказывательных формул достаточно показать, что импликация 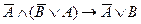 , тождественно истинна (или тавтология).
, тождественно истинна (или тавтология).
Докажем это с помощью преобразований:
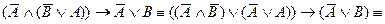
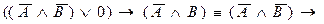
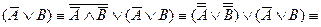
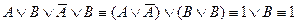
3-й способ. Методом от противного. Предположим, что формула 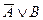 не является логическим следствием формул
не является логическим следствием формул 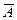 и
и 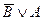 . Значит, при истинных посылках
. Значит, при истинных посылках 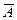 и
и 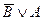 формула
формула 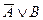 принимает значение 0. Т.к.
принимает значение 0. Т.к. 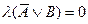 , то
, то 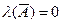 ,
, 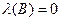 . Но тогда мы получаем противоречие с предположением об истинности посылки
. Но тогда мы получаем противоречие с предположением об истинности посылки 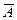 . Полученное противоречие доказывает, что наше предположение неверно, и значит, формула
. Полученное противоречие доказывает, что наше предположение неверно, и значит, формула 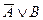 является логическим следствием посылок
является логическим следствием посылок 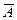 и
и 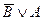 .
.
Приложения алгебры высказываний
Алгебра высказываний нашла применение в логико-математической практике. Во-первых, при анализе и синтезе контактных схем.
П р и м е р 15.Упростить релейно-контактную схему и определить условия ее работы.
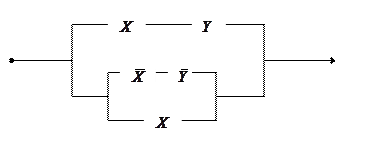
Решение. Запишем функцию проводимости этой схемы и преобразуем ее с помощью основных равносильностей алгебры высказываний.
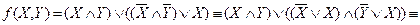
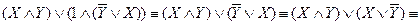
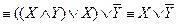
По новой функции проводимости строим упрощенную схему:
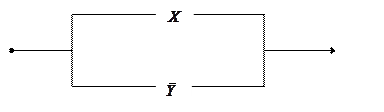
Из полученной формулы, очевидно, что 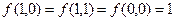 . Это и есть условия работы данной схемы.
. Это и есть условия работы данной схемы.
П р и м е р 16. Для комитета, состоящего из 4 человек сконструировать электрическую цепь так, чтобы лампочка зажигалась, если за данное предложение проголосовало меньшинство.
Решение. 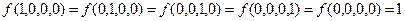 Для данных условий работы составим функцию проводимости:
Для данных условий работы составим функцию проводимости:
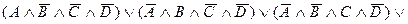
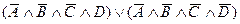
Схема будет такой:
 |


Во-вторых, в математике часто приходится формулировать утверждения, которые являются отрицаниями других утверждений, Обычно трудности вызывают формулировки отрицаний сложных предложений, в которых присутствует импликация. Процесс нахождения удобной формулировки отрицания некоторого предложения в алгебре высказываний получил название построения отрицания. Чаще всего для формулы 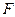 , имеющей в записи импликации, построить отрицание означает следующее: для формулы
, имеющей в записи импликации, построить отрицание означает следующее: для формулы 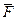 найти равносильную и по возможности простую формулу
найти равносильную и по возможности простую формулу 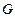 , в которой нет импликаций, а знаки отрицания (если они есть) относятся только к атомам. При построении отрицаний большую роль играют законы де Моргана, закон исключения импликации, закон двойного отрицания.
, в которой нет импликаций, а знаки отрицания (если они есть) относятся только к атомам. При построении отрицаний большую роль играют законы де Моргана, закон исключения импликации, закон двойного отрицания.
П р и м е р 17. Перевести предложение «Если я устал или голоден, то не могу заниматься» на логический язык, построить его отрицание и сформулировать это отрицание по-русски.
Введем атомы: 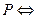 «Я устал»,
«Я устал», 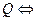 «Я голоден»; наконец,
«Я голоден»; наконец, 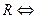 «Я могу заниматься». Тогда заданное предложение запишется формулой
«Я могу заниматься». Тогда заданное предложение запишется формулой 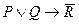 . Далее
. Далее 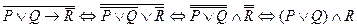
Значит, отрицание предложения формулируется так: «Я либо устал, либо голоден, но могу заниматься».
В-третьих, аппарат алгебры высказываний позволяет выяснять правильность выводов из некоторого списка положений.
П р и м е р 18. Проанализировать правильность вывода в рассуждении: «Если Коля дома, то у него горит свет и отрыто окно. Свет у Коли не горит. Значит, его нет дома».
Введем атомы: 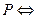 «Коля дома»,
«Коля дома», 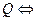 «У Коли горит свет»;
«У Коли горит свет»; 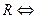 «У Коли открыто окно». Тогда заданное рассуждение запишется в виде
«У Коли открыто окно». Тогда заданное рассуждение запишется в виде 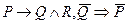 . Чтобы убедиться в его правильности, достаточно показать, что формула
. Чтобы убедиться в его правильности, достаточно показать, что формула 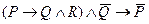 является тождественно истинной. Имеем:
является тождественно истинной. Имеем: 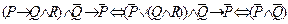
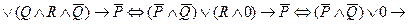
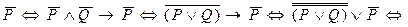
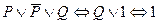 .
.
И, наконец, с помощью алгебры высказываний можно решать различные логические задачи.
Обобщённый приём решения логических задач методом алгебры высказываний:
1.Выделяем и обозначаем все участвующие в задаче простые высказывания;
2. Строим из них содержащиеся в условии задачи сложные высказывания;
3.Рассматриваем конъюнкцию построенных посылок, она истинна по условию;
4,Преобразуем эту конъюнкцию с помощью логических равенств к более простому виду, удобному для получения требуемой в задаче информации;
5. Извлекаем эту информацию (ответы на вопросы задачи).
Воспользуемся данным приёмом при решении логической задачи.
П р и м е р 19. Согласно инструкции капитан должен находиться на судне всегда, за исключением случаев, когда с судна выгружают груз; если же груз не выгружают, то рулевой никогда не отсутствует, если не отсутствует капитан. В каких случаях рулевой обязан присутствовать на судне?
Решение. 1. Введём обозначения, соответствующие простым высказываниям: 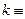 «Капитан присутствует на судне»;
«Капитан присутствует на судне»; 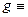 «С судна выгружают груз»;
«С судна выгружают груз»; 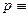 «Рулевой присутствует на судне».
«Рулевой присутствует на судне».
2. В инструкции могут быть выделены одно простое и два сложных высказывания: 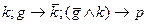 .
.
3. 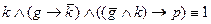 .
.
4. Упростим данную конъюнкцию: 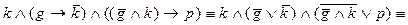
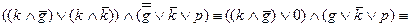
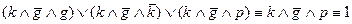 .
.
5. Ответ: Если с судна не выгружают груз, то рулевой обязан присутствовать вместе с капитаном.
П р и м е р 20. Три девушки: Аля, Валя и Катя ходили в театр. Одна из них была в красном платье, другая – в белом, третья – в синем. На вопрос, какое на каждой из девушек было платье, они дали ответ: Аля была в красном, Катя – не в синем, Валя – не в красном. В этом ответе из трех частей одна верна, две – не верны. В каком платье была каждая из девушек?
Решение. Введем обозначения:
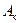 – Аля в красном платье;
– Аля в красном платье;
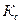 – Катя в синем платье;
– Катя в синем платье;
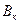 – Валя в красном платье, и тогда ответ, который дали девушки, можно записать в виде конъюнкции
– Валя в красном платье, и тогда ответ, который дали девушки, можно записать в виде конъюнкции 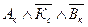 . Так как по условию в этом ответе из трех частей одна верна, а две не верны, то истинна следующая дизъюнкция:
. Так как по условию в этом ответе из трех частей одна верна, а две не верны, то истинна следующая дизъюнкция:
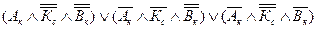 .
.
Упростив эту формулу, получаем
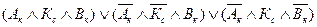 .
.
Поскольку первая и третья конъюнкции ложны, то истинна 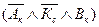 , то есть: Валя в красном платье, Катя в белом платье, Аля в синем платье.
, то есть: Валя в красном платье, Катя в белом платье, Аля в синем платье.
 2015-05-13
2015-05-13 1694
1694
