| Физическая величина или закон | Формула |
| Показатель преломления среды | 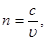 где n – показатель преломления среды, с - скорость распространения света в вакууме, где n – показатель преломления среды, с - скорость распространения света в вакууме, 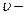 скорость распространения света в среде скорость распространения света в среде |
| Оптическая длина пути луча | L=n l, где L – оптическая длина пути луча, n – показатель преломления среды, l – геометрическая длина луча |
| Оптическая разность хода волн | 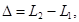 где ∆ - оптическая разность хода волн, L – оптическая длина пути луча где ∆ - оптическая разность хода волн, L – оптическая длина пути луча |
| Условие максимума (усиления) света при интерференции | 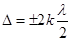 , k = 0,1,2,3 …, где ∆ - оптическая разность хода, λ – длина волны , k = 0,1,2,3 …, где ∆ - оптическая разность хода, λ – длина волны |
| Условие минимума (ослабления) света при интерференции | 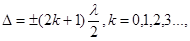 где ∆ - оптическая разность хода, λ – длина волны где ∆ - оптическая разность хода, λ – длина волны |
| Линейное и угловое расстояния между соседними интерференционными полосами на экране | 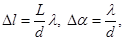 где L – оптическая длина пути луча, l – линейное расстояние между полосами на экране, λ – длина волны, d – расстояние между источниками, ∆λ – угловое расстояние между полосами на экране где L – оптическая длина пути луча, l – линейное расстояние между полосами на экране, λ – длина волны, d – расстояние между источниками, ∆λ – угловое расстояние между полосами на экране |
| Оптическая разность хода волн в тонких пленках в отраженном и проходящем свете | 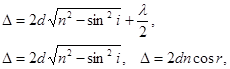 где ∆ - оптическая разность хода, λ – длина волны, d – толщина, n – показатель преломления среды, i – угол падения волны, r — угол преломления где ∆ - оптическая разность хода, λ – длина волны, d – толщина, n – показатель преломления среды, i – угол падения волны, r — угол преломления |
| Разрешающая сила дифракционной решетки | 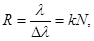 где R - разрешающая сила дифракционной решетки, λ – длина волны, N — число штрихов решетки, ∆λ – изменение длины волны, k — порядковый номер дифракционного максимума где R - разрешающая сила дифракционной решетки, λ – длина волны, N — число штрихов решетки, ∆λ – изменение длины волны, k — порядковый номер дифракционного максимума |
| Световой поток Ф, испускаемый изотропным источником в пределах телесного угла ω | Ф = I ω, где Ф – световой поток, ω – телесный угол, I – сила света |
| Освещенность поверхности | E = Ф / S, где Е – освещенность поверхности, Ф – световой поток, S – площадь поверхности |
| Освещенность, создаваемая изотропным источником света | 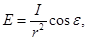 где Е – освещенность поверхности, I – сила света источника, ε — угол падения лучей, r — расстояние от поверхности до источника света где Е – освещенность поверхности, I – сила света источника, ε — угол падения лучей, r — расстояние от поверхности до источника света |
| Яркость светящейся поверхности | В = I / ΔS, где В – яркость, I – сила света, |
| Светимость поверхности | R = Ф / S, где R – светимость поверхности, Ф – световой поток, S – площадь поверхности |
| Светимость косинусных излучателей | R = π B, где R – светимость, В – яркость |
| Условие главных максимумов дифракционной решетки | 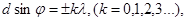 где d – период дифракционной решетки, k – порядок главного максимума, φ - угол дифракции, λ – длина волны где d – период дифракционной решетки, k – порядок главного максимума, φ - угол дифракции, λ – длина волны |
| Условие дифракционных максимумов от одной щели | 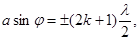 где α – ширина щели, k – порядок максимума, λ – длина волны, φ - угол дифракции где α – ширина щели, k – порядок максимума, λ – длина волны, φ - угол дифракции |
| Условие дифракционных минимумов от одной щели | 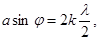 где α – ширина щели, k – порядок минимума, λ – длина волны, φ - угол дифракции где α – ширина щели, k – порядок минимума, λ – длина волны, φ - угол дифракции |
| Закон Брюстера | 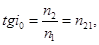 где где 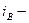 угол падения, n2, n1 –показатели преломления первой и второй среды. угол падения, n2, n1 –показатели преломления первой и второй среды. |
| Закон Малюса | 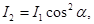 где I1 – интенсивность света, падающего на анализатор, I2 – интенсивность света, вышедшего из анализатора, α – угол между плоскостями поляризатора и анализатора где I1 – интенсивность света, падающего на анализатор, I2 – интенсивность света, вышедшего из анализатора, α – угол между плоскостями поляризатора и анализатора |
| Формула Вульфа-Брегга | 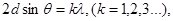 где d – расстояние между атомными плоскостями кристалла, θ – угол скольжения, λ – длина волны где d – расстояние между атомными плоскостями кристалла, θ – угол скольжения, λ – длина волны |
| Угол вращения плоскости поляризации в кристаллах и растворах | 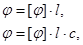 где φ - угол вращения плоскости поляризации, l – длина пути света в оптически активном веществе, с – скорость света где φ - угол вращения плоскости поляризации, l – длина пути света в оптически активном веществе, с – скорость света |
| Закон Стефана-Больцмана | 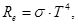 где Re – энергетическая светимость, σ – постоянная Стефана-Больцмана, Т - температура где Re – энергетическая светимость, σ – постоянная Стефана-Больцмана, Т - температура |
| Закон смещения Вина | 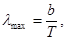 где λmax – длина волны с максимальным значением спектральной плотности энергетической светимости черного тела, b – постоянная Вина, Т - температура где λmax – длина волны с максимальным значением спектральной плотности энергетической светимости черного тела, b – постоянная Вина, Т - температура |
| Энергия фотона | 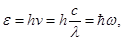 где h – постоянная Планка, ν – частота, λ – длина волны, с – скорость света, где h – постоянная Планка, ν – частота, λ – длина волны, с – скорость света, 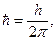 ω – частота излучения ω – частота излучения |
| Импульс фотона | 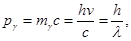 где где 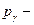 импульс фотона, импульс фотона, 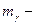 масса фотона, с – скорость света, h – постоянная Планка, ν – частота, λ – длина волны масса фотона, с – скорость света, h – постоянная Планка, ν – частота, λ – длина волны |
| Давление света при нормальном падении | 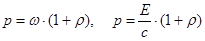 |
| Уравнение Эйнштейна для внешнего фотоэффекта | hv=A+T, где h – постоянная Планка, ν – частота излучения, А – работа выхода, T – кинетическая энергия фотоэлектрона |
| при T < 5 кэВ | 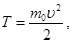 где T – кинетическая энергия электрона, где T – кинетическая энергия электрона, 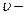 скорость электрона, т0 – масса покоя электрона скорость электрона, т0 – масса покоя электрона |
| при T > 5 кэВ | 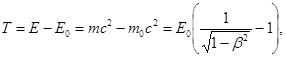 где T – кинетическая энергия, т0 – масса покоя электрона, т – масса электрона, Е – энергия электрона, Е0 – энергия покоя электрона, где T – кинетическая энергия, т0 – масса покоя электрона, т – масса электрона, Е – энергия электрона, Е0 – энергия покоя электрона, 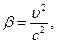 т0 – масса покоя электрона т0 – масса покоя электрона |
| Изменение длины волны при эффекте Комптона | 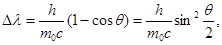 где ∆λ – изменение длины волны, h – постоянная Планка, с – скорость света, θ – угол рассеивания фотона, т0 – масса электрона отдачи где ∆λ – изменение длины волны, h – постоянная Планка, с – скорость света, θ – угол рассеивания фотона, т0 – масса электрона отдачи |
| Формула Бальмера | 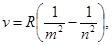 где ν – частота испускаемого света, R - постоянная Ридберга, n, m - номера орбит электрона(m=1,2,3…), (n=m+1) где ν – частота испускаемого света, R - постоянная Ридберга, n, m - номера орбит электрона(m=1,2,3…), (n=m+1) |
| Момент импульса электрона на стационарных орбитах | 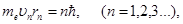 где где 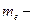 масса электрона, масса электрона, 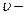 скорость электрона, скорость электрона, 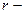 радиус орбиты радиус орбиты |
| Второй постулат Бора | 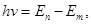 где h – постоянная Планка, ν – частота испускаемого света, En – энергия атома до излучения/поглощения, Em - энергия атома после излучения/поглощения где h – постоянная Планка, ν – частота испускаемого света, En – энергия атома до излучения/поглощения, Em - энергия атома после излучения/поглощения |
| Соотношения неопределенностей |  где ∆х – неопределенность координаты микрочастицы, ∆р - соответствующая координате неопределенность проекции импульса, h – постоянная Планка, ∆Е – неопределенность энергии некоторого состояния системы, ∆t - время где ∆х – неопределенность координаты микрочастицы, ∆р - соответствующая координате неопределенность проекции импульса, h – постоянная Планка, ∆Е – неопределенность энергии некоторого состояния системы, ∆t - время |
| Длина волны де Бройля | 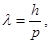 где λ – длина волны, h – постоянная Планка, р – импульс микрочастицы где λ – длина волны, h – постоянная Планка, р – импульс микрочастицы |
| Стационарное уравнение Шредингера | 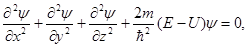 где ψ – волновая функция частицы, где ψ – волновая функция частицы, 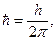 h – постоянная Планка, U – потенциальная функция частицы в силовом поле, Е – энергия частицы, x,y,z – координаты частицы, т – масса частицы, h – постоянная Планка, U – потенциальная функция частицы в силовом поле, Е – энергия частицы, x,y,z – координаты частицы, т – масса частицы, 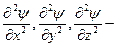 вторые частные производные волновой функции по координатам вторые частные производные волновой функции по координатам |
| Вероятность обнаружения частицы в интервале от x 1 до x 2 | 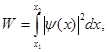 где W – вероятность, ψ – волновая функция частицы где W – вероятность, ψ – волновая функция частицы |
| Собственное значение энергии E n частицы, находящейся на n -ом энергетическом уровне в бесконечно глубоком одномерном потенциальном ящике | 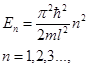 где где 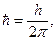 h – постоянная Планка, т – масса частицы, n – главное квантовое число, l – орбитальное квантовое число h – постоянная Планка, т – масса частицы, n – главное квантовое число, l – орбитальное квантовое число |
| Соответствующая этой энергии собственная волновая функция имеет вид | 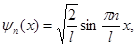 где ψ – волновая функция частицы, n – главное квантовое число, l - орбитальное квантовое число, х - координата частицы где ψ – волновая функция частицы, n – главное квантовое число, l - орбитальное квантовое число, х - координата частицы |
| Коэффициенты отражения ρ и пропускания τ волн де Бройля через низкий (U < E) потенциальный барьер бесконечной ширины | 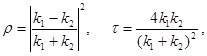 где где 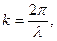 λ – длина волны λ – длина волны |
| Коэффициент прозрачности D прямоугольного потенциального барьера конечной ширины | 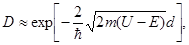 где U – высота потенциального барьера, т – масса частицы, где U – высота потенциального барьера, т – масса частицы, 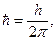 h – постоянная Планка, Е – энергия частицы h – постоянная Планка, Е – энергия частицы |
Основные формулы и законы
|
|

Сейчас читают про:
 2015-06-05
2015-06-05 723
723







