Равнобедренная трапеция с основаниями 10 и 4 единиц имеет острый угол 300.
Написать уравнения сторон трапеции, приняв за ось ОХ меньшее основание трапеции,
а за ось ОУ ось симметрии трапеции
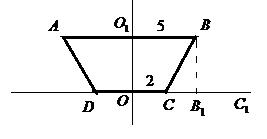
Рис.7
Замечание. К задаче 3 удобнее записать краткие условия после выполнения чертежа
Дано:
АВСD –равнобедренная трапеция,
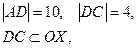
DC – меньшее основание, ось ОУ – ось симметрии трапеции
Составить уравнения сторон
Решение
1Составим уравнение стороны DC (рис.7)
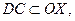 тогда DC определяется уравнением
тогда DC определяется уравнением 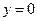
2 Составим уравнение стороны СВ
Т.к по условию трапеция равнобедренная, то 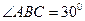 , тогда
, тогда 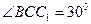 (рис.7)
(рис.7)
(углы равны как внутренние на крест лежащие), следовательно 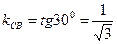 .
.
По условию ОУ ось симметрии трапеции, тогда 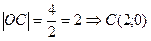
Воспользуемся уравнением «пучка»
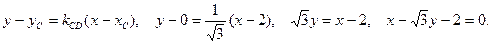
3 Составим уравнение стороны АD
По условию трапеция равнобедренная, то 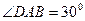 , тогда
, тогда 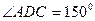 (рис.3), следовательно
(рис.3), следовательно 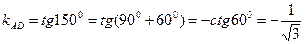
По условию ОУ ось симметрии трапеции, тогда 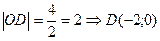 ,т.к. направление отрицательное.
,т.к. направление отрицательное.
Воспользуемся уравнением «пучка»
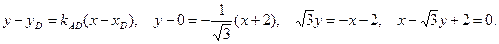
4 Составим уравнение стороны АВ
4.1 Найдем координаты точки В:
по условию ОУ ось симметрии трапеции, тогда 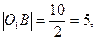 проекция
проекция 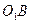 на ось ОХ
на ось ОХ
(рис.7) равна 5, тогда 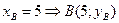 .
.
Точка В лежит на прямой СВ, её координаты удовлетворяют уравнению СВ:
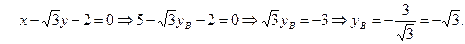
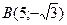
4.2 Составим уравнение стороны АВ:
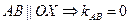
Воспользуемся уравнением «пучка»
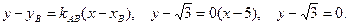
Ответ: 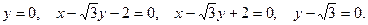
Задача 8
Найти проекцию точки 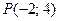 на прямую, проходящую через точку
на прямую, проходящую через точку 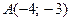 и отсекающую на осях координат равные отрезки.
и отсекающую на осях координат равные отрезки.
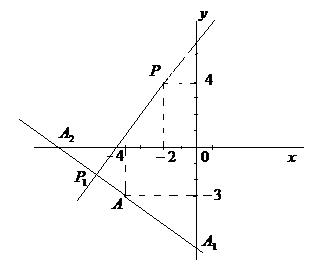
Рис.9
Решение
1 Составим уравнение прямой 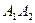 (рис.9)
(рис.9)
Т.к. по условию прямая 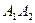 отсекает на осях координат равные отрезки,
отсекает на осях координат равные отрезки,
воспользуемся уравнений прямой в «отрезках». Пусть 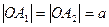 , тогда
, тогда
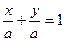 (*)
(*)
Точка А(-4;-3) лежит на прямой 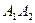 , значит её координаты удовлетворяют уравнению (*)
, значит её координаты удовлетворяют уравнению (*)
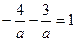 ,
,
Откуда найдем:
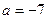
Подставим в уравнение (*)
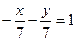
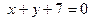 (**)
(**)
2 Составим уравнение 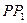 (рис.9)
(рис.9)
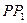 ^
^ 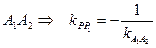
Из уравнения (**) имеем: 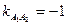 , тогда
, тогда 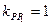
Воспользуемся уравнением «пучка»
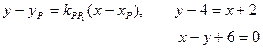
3 Найдем 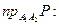
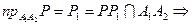
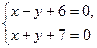
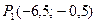
Ответ: 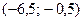
Приложение А
Основные уравнения прямой на плоскости

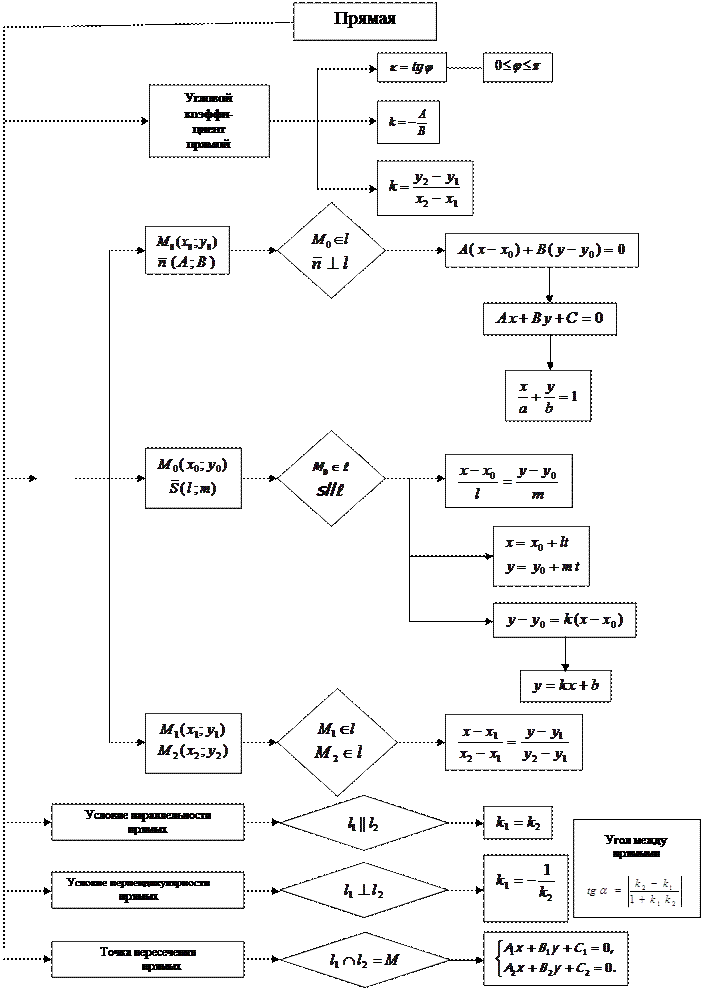
Приложение Б
Приложение А
АЛГОРИТМ
Составление уравнения медианы треугольника
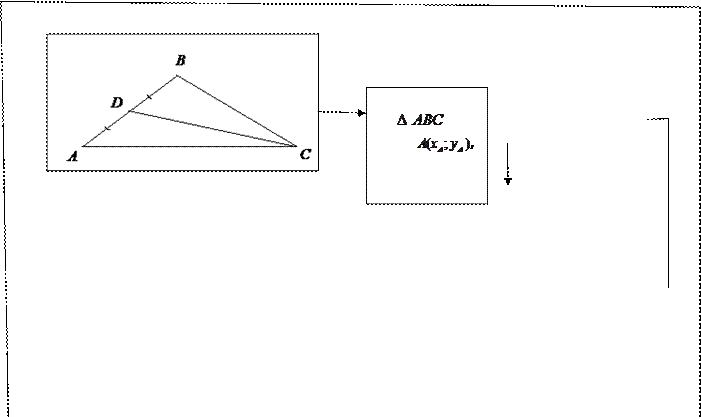
|


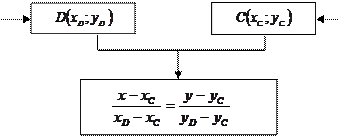 | ||||
 | ||||
 |
Приложение В
АЛГОРИТМ
Составление уравнения средней линии треугольника
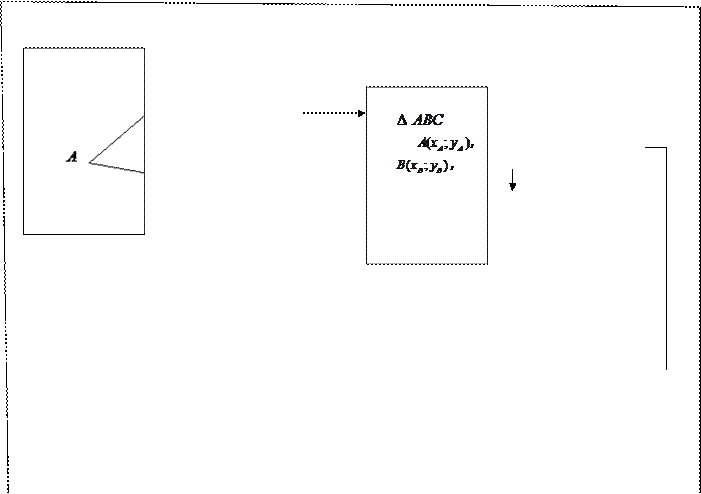
|
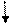
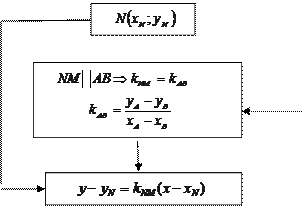 | ||||
 | ||||
 |
Приложение Г
АЛГОРИТМ
Составление уравнения высоты треугольника
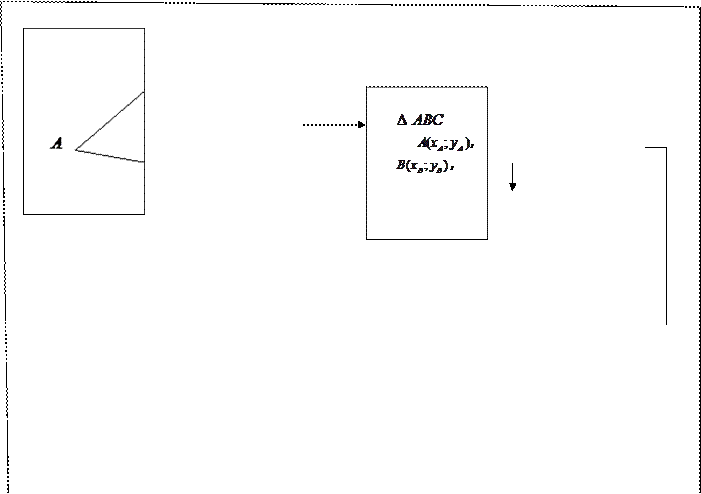
|
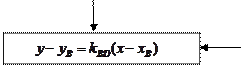 | ||||
 | ||||
 |
Приложение Д
АЛГОРИТМ
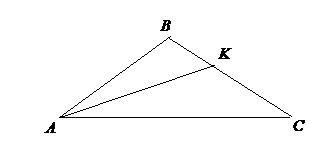
Составление уравнения биссектрисы треугольника
 |  |

|
|



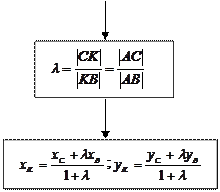 |
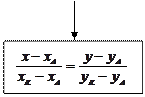 |
 |
 2015-06-28
2015-06-28 3525
3525
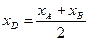 ,
, 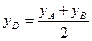
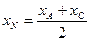 ,
, 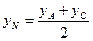
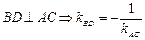
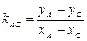
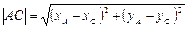
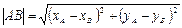
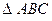
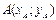 ,
, 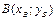 ,
, 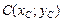
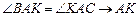 биссектриса
биссектриса